用正交变换化实二次型为标准形的同步求解问题

李延敏, 张 力

(1.吉林财经大学应用数学学院,长春 130117; 2.东北师范大学物理学院,长春 130024)

用正交变换化实二次型为标准形的同步求解问题

李延敏1, 张 力2

(1.吉林财经大学应用数学学院,长春 130117; 2.东北师范大学物理学院,长春 130024)

作为《关于矩阵的特征值与特征向量同步求解问题》的续篇,利用其给出的方法,证明了新的定理.通过对实对称矩阵进行行列互逆变换,同步求出二次型的标准形及正交变换阵,简化了复杂的施密特正交化法,较好地解决了二次型标准形与正交变换阵同步求解问题.

二次型;标准形;互逆变换;正交变换;同步求解

用正交变换化二次型为标准形的问题,一般总是由特征方程求特征值要解带参数的行列式,而且只有先求出特征值方可由方程组求特征向量,进而再用复杂的施密特正交化法求出正交变换阵,非常繁琐.所以,用正交变换化二次型为标准形的新方法研究引起了广泛的兴趣,如文[3]用增加约束方程解决了正交化问题;文[4]用初等变换法化二次型为标准形;文[5]用分块阵求二次型的标准形等.但仍没有摆脱带参数行列式化简和标准形与正交变换阵同步求解问题。本文继续作者文[1]中的研究,给出了对原矩阵作行列互逆变换就可同步求出特征值和特征向量及特征向量的正交化和单位化的深化方法,较好地解决了二次型标准形与正交变换阵同步求解问题,而且不需要考虑带参数的特征矩阵及单独进行的复杂的施密特正交化.

为了定理的叙述方便,将文[1]中重要定义、定理、方法列于此,便于推论和新定理的引进.

定义1 矩阵的行列互逆变换:

矩阵的下列三种变换称为行列互逆变换:

(i)互换i,j两行,同时互换i,j列;

(iii)第i行k倍加入第j行,同时第j列-k倍加入第i列.

定理1 A为n阶可对角化矩阵,并且

为解决同步求出二次型的标准形及正交变换阵问题,本文给出[1]中定理1的两个推论及定理3.

推论1 若定理1中A是实对称矩阵,且D=diag(λ1,λ2,…,λn)中的λi(i=1,…,n)互不相同时,则由[2]中定理知中的βi与βj相互正交(i≠j).对PT的行进行单位变换,使

推论2 若定理1中,A是实对称矩阵,且D=diag(λ1,λ2,…,λn)中的λi有重根时,不妨λ1有k重根,其他为单根,此时

其中βi(i=1,…,k)与βj(j=k+1,…,n)正交,且βj(j=k+1,…,n)相互正交,但β1,…,βk之间不一定正交.计算内积βiβTi(i=1,…,k),求出值最小者,不妨β1β最小.做如下行列互逆变换

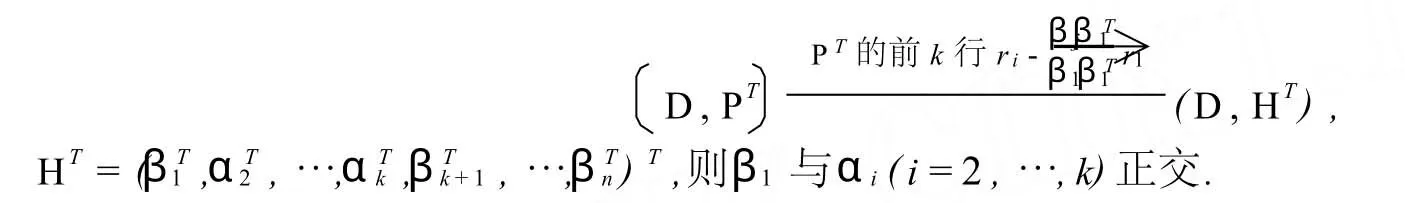
推论2优化了施密特正交化法,实际计算中只需重复利用推论2的方法即可得到β1,…,βk的正交化.

定理3 A为二次型f=XTAX的实对称矩阵,则只需对A行列互逆变换化为对角阵D,对单位阵En只做相同的行变换即可化为正交阵UT,即

由于推论1、推论2中的计算方法并没有改变定理1中所得到的最基本结论,即λ1,…,λn为A的全部特征值,α为A的对应特征值λi的特征向量,且新方法得到α,…,α是标准正交基,则由[2]中定理知:二次型的标准形为

利用定理3的方法可解决正交变换与二次型标准形同步求解问题,不仅不用求带参数的行列式且避开了复杂的施密特正交化法,只需简单行变即可正交化,不用进行施密特正交化法的其他步骤.下面举例说明定理3的用法.

为了运算上的方便,这里约定:

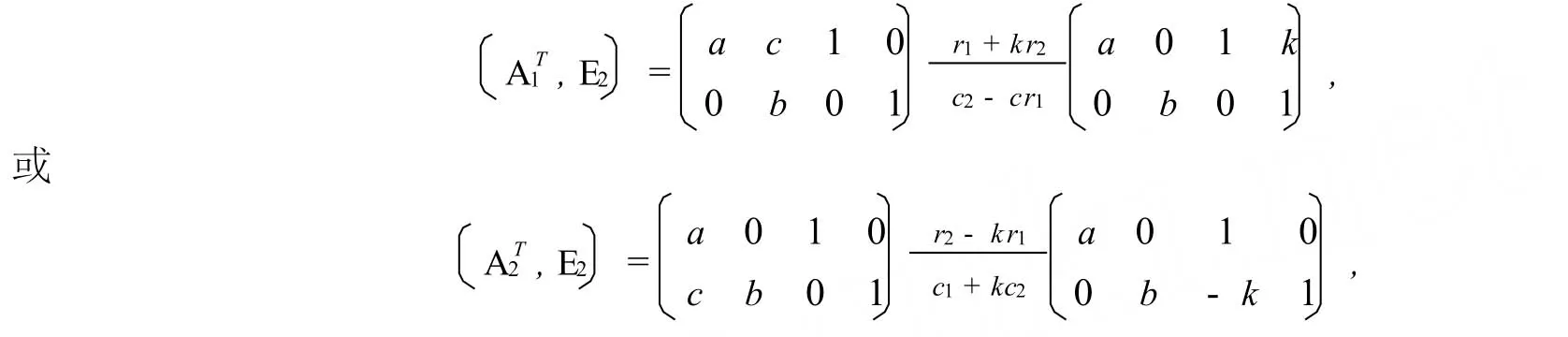
例1 用正交变换化下列二次型为标准形,并求出标准形及正交变换:

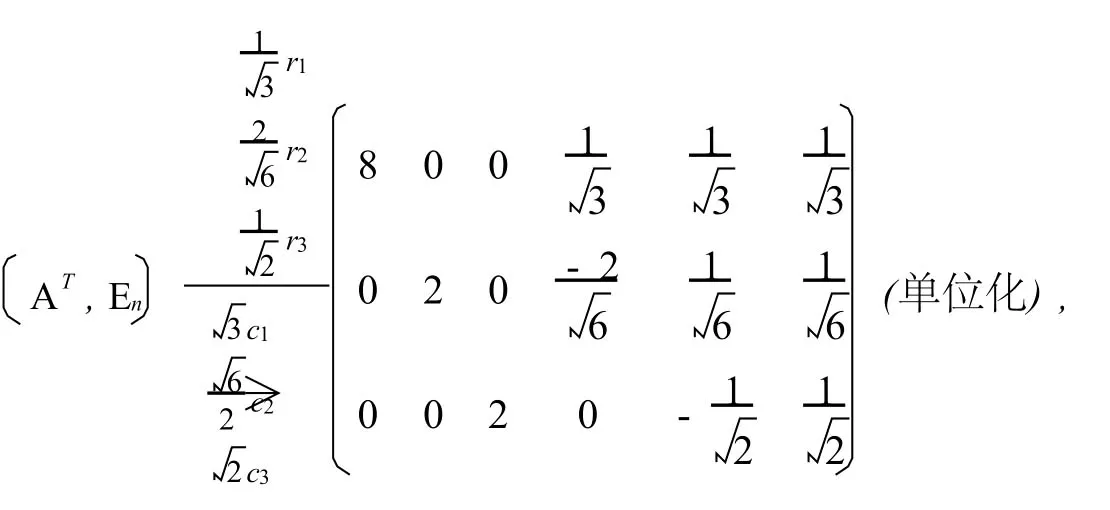
所以二次型的标准形为

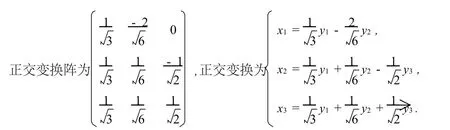
例2 用正交变换化下列二次型为标准形,并求出标准形及正交变换:

通过以上例题求解可以看出,用该方法解决了二次型的标准形及正交变换矩阵同步求解问题,尤其是对实对称矩阵的相同特征值对应的不正交特征向量的初等变换正交化法,简洁实用.

[1] 李延敏.关于矩阵的特征值与特征向量同步求解问题[J].大学数学,2004,20(4)：92-95.

[2] 北京大学数学系几何与代数教研室代数小组.高等代数[M].3版.北京：高等教育出版社,2003.

[3] 王琳.用正交变换化实二次型为标准型方法研究[J].数学通报,1990,30(3)：31-33.

[4] 汪庆丽.用矩阵的初等变换化实二次型为标准形[J].新疆教育学院学报,2001,17(2)：22-24.

[5] 曹庆刚.用分块矩阵求合同与求逆[J].数学通报,1990,30(10)：28-32.

The Synchronization Solution of Transforming the Real Quadratic Forms into the Canonical Forms with Orthogonal Transformation

L I Yan-min1, Z HA N G L i2
(1.School of Applied mathematics,Jilin University of Finance and Economics,Changchun 130117,China; 2.School of Physics,Northeast Normal University,Changchun 130024,China)

As the sequel of the paper“On the Cogradient Solving Question of Eigenvalue and Eigenvector of a Matrix”,in this paper,the author proved new theorems with the use of the methods given in the paper.Through carrying on reciprocal transformation of the rows and columns to the real symmetric matrix,the author obtained the standard forms and the orthogonal transformation matrix of the quadratic forms simultaneously,simplified the complex Schmidt orthogonalization method and solved well the synchronization solution problem of the canonical forms and the orthogonal transformation matrix of the quadratic forms.

quadratic forms;canonical forms;reciprocal transformation;orthogonal transformation;synchronized solution

O151.21

C

1672-1454(2011)05-0167-05

2008-11-04;[修改日期]2009-03-03

吉林省教育科学“十一五”规划重点项目(ZC0148);吉林省教育厅重点教研项目(吉高教字[2008]41号2008193);吉林省自然科学基金项目(20101599)