平面波斜入射到有孔腔体的屏蔽效能分析

石 丹

（北京邮电大学，北京100876）

1.引 言

屏蔽是抑制电磁干扰的有效方法，它能防止不希望的电磁能量耦合到敏感设备。通常采用屏蔽效能参数衡量屏蔽体的屏蔽效果。但屏蔽效能与屏蔽体的完整性密切相关，如果屏蔽体由于通风、散热或信号连接出现孔缝时，屏蔽体的屏蔽效能会随之下降，因此计算有孔屏蔽体的屏蔽效能成为了研究的热点。目前采用数值建模是解决该问题的主要手段之一，包括传输线矩阵（TLM）[1]，时域有限差分（FDTD）[2－3]及矩量法 Mo M[4]，这些方法能够计算较为复杂的屏蔽体结构，但缺点在于不能直观反映屏蔽效能与孔缝尺寸、位置及入射频率等参量的函数关系。近来，等效传输线法被广泛应用于分析有孔屏蔽腔的屏蔽效能[6－14]，该方法能简单明确给出屏蔽效能的解析计算公式。Robinson最早将等效传输线法用于有孔腔体的屏蔽效能分析，但其研究的问题仅限于缝隙处于腔体中心情况，且没有考虑高次模的影响，因此不能应用于较高频率[6]。文献[7] [8] 虽然分析了缝隙偏离腔体中心的情况，但忽略了腔体壁产生的损耗。文献[9] 虽然考虑了高次模和腔体壁损耗的影响，但仅限于缝隙处于腔体壁中心的情况。而且，文献[6] －[14] 都仅适用于垂直入射平面波的情况，本文得到的公式考虑了缝隙偏离腔体壁中心、腔体壁存在损耗、高次模产生的影响、及平面波以任意角度和极化方向入射的普遍情况。

2.理论计算

有孔屏蔽腔的长、宽、高为a、b、d，腔体壁上缝隙的长和宽为l、w.平面波以角度θ入射到腔体带缝表面，θ为入射波与腔体壁法线方向的夹角，电场极化方向与入射平面（入射方向与法线方向构成的平面）的夹角为φ.以任意方向入射的电场可以分解成相互垂直的两个分量，一个分量E//平行于入射平面，另一分量E⊥垂直于入射平面。分别考虑这两个分量产生的影响，最后将其合成得到总场强。

分析过程可以分解为以下三个步骤：

1）将任意极化的电场矢量分解为相互垂直的E//和E⊥两个分量，然后得到两个分量穿过缝隙后的大小。

2）利用高次模等效传输线方法分析场量在腔体中的传播。

3）将平行极化分量和垂直极化分量合成得到腔体内测试点处的总电场，最后求出有孔屏蔽腔的屏蔽效能。

2.1 穿过缝隙的场强

将任意方向的电场分量分解为平行极化分量E//和垂直极化分量E⊥，其大小为

根据电磁场理论[15]，平面波在介质中的传输系数为

2.1.1 垂直极化分量

对于穿过缝隙的垂直极化分量，等式（3）中的Z2为

式中Zap为缝隙的等效阻抗，其大小为

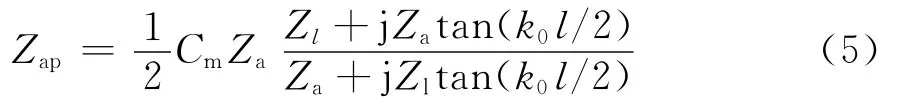
根据缝隙的场均匀性，耦合系数Cm为

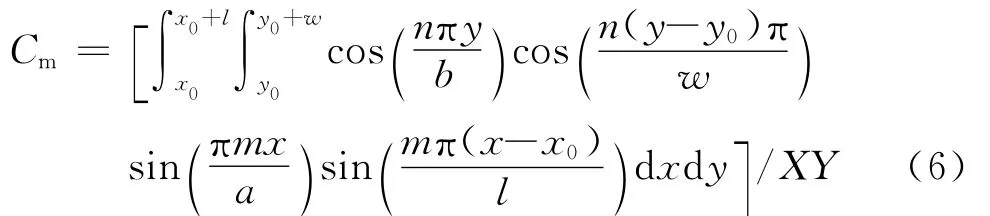
其中X和Y为缝隙的中心位置坐标，如图1所示。

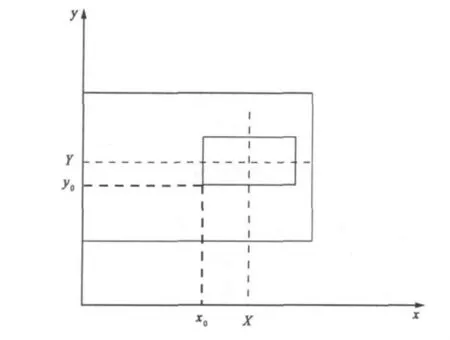
图1 缝隙的坐标图

Za为缝隙的特性阻抗，根据Gupta理论[16]，其大小为

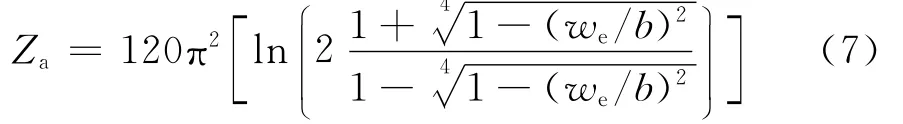
有效宽度we为

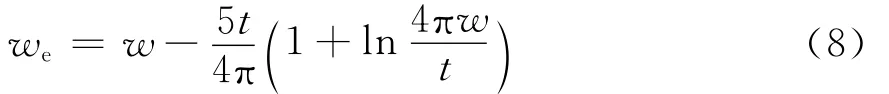
其中t为腔体壁厚度，w为缝隙宽度。

θT为进入缝隙的折射波与腔体壁法线方向的夹角，表达式为

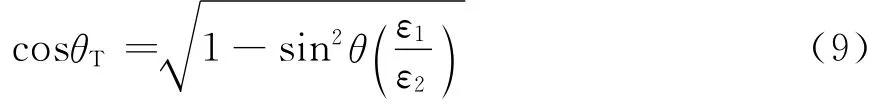
θ为平面波的入射角度，ε1为空气的介电常数，ε2为缝隙的等效介电常数，数值可由式（10）得到

μ0为空气的磁导率。

等式（3）中的Z1等于Z0/cosθ，Z0为空气波阻抗，大小等于377欧。Zl代表腔体壁的表面阻抗。

将式（4）～（10）代入到等式（3），即可求出传输系数T⊥，则垂直极化分量穿过缝隙后衰减为

2.1.2 平行极化分量

对于穿过缝隙的平行极化分量

Zap，Z0，θ，cosθT等参数与2.1.1部分相同。

将式（5）～（10）和（12）～（13）带入等式（3），可以得到传输系数T//，然后利用等式（14）即可得到平行极化分量穿过缝隙后的大小。

2.2 场分量在腔体中的传播

将穿过缝隙的场分量作为等效源，则等效源阻抗如式（15）所示。

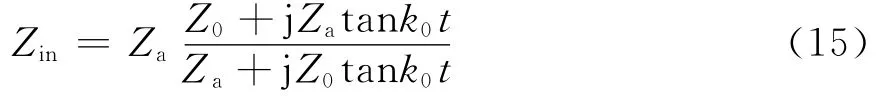
式中：Za为缝隙特性阻抗；Z0为空气波阻抗；t为腔体壁厚度。

对于传播的TEmn模式，其特性阻抗和传播常数为[17－18]

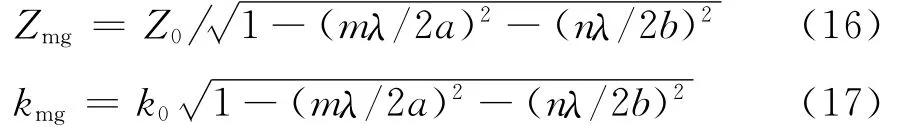
2.2.1 垂直极化分量

垂直极化分量在腔体内传播的等效电路如图2所示。

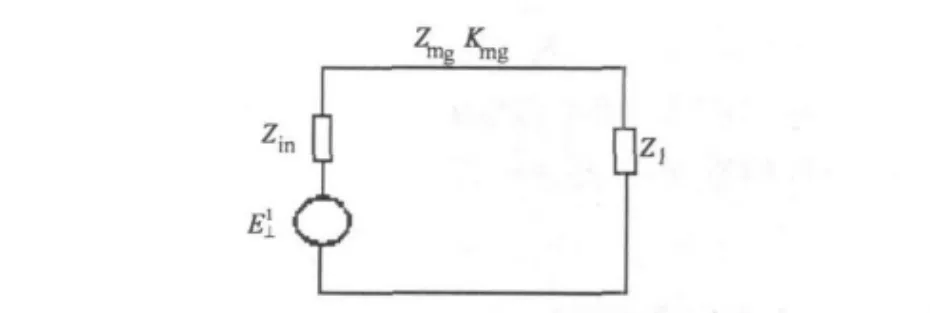
图2 等效电路

图2中终端阻抗Zl代表腔体壁的表面阻抗，其大小为

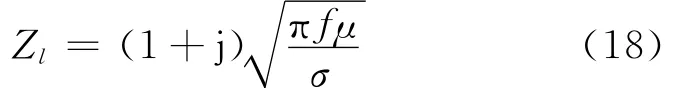
式中σ和μ分别为腔体壁材料的电导率和磁导率。考虑终端阻抗Zl表明屏蔽效能的计算公式包括了腔体壁损耗。对于电导率为无穷大的理想导体，其表面阻抗Zl为零。

将、Zin及终端阻抗Zl变换到腔体中的测试点P，从而得到了等效源V2、源阻抗Z2及终端负载Z3：

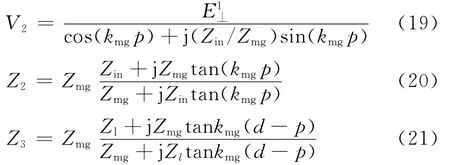
根据等式（15）～（21），P点的电压为

考虑到腔体内的高次模，P点的总电压为

2.2.2 平行极化分量

平行极化分量在腔体内传播时，其等效电路如图3所示

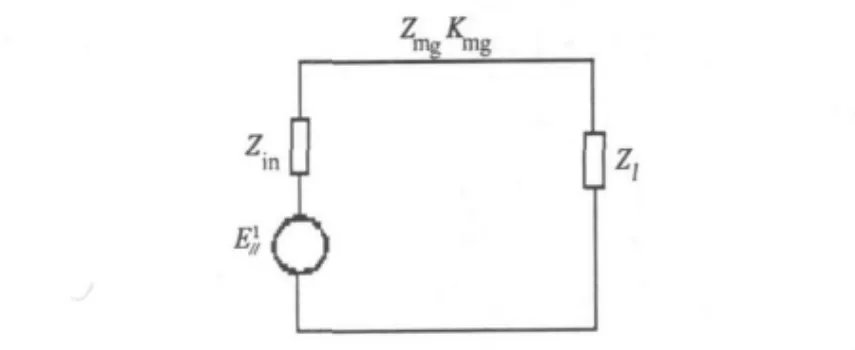
图3 等效电路

将穿过缝隙的平行极化分量变换到测试点P，得到等效电压V3为

根据等式（15）～（18），（20）～（21）及（24），P点的电压为

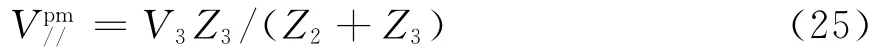
考虑腔体中的其他模式，可以得到由于平行极化分量的影响P点总电压为

2.3 有孔腔体屏蔽效能

将平行极化分量和垂直极化分量合成得到P点的总电压

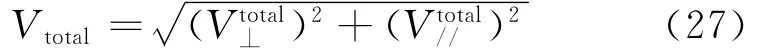
没有屏蔽腔时P点的终端负载为Z0，则根据分压公式，P点的电压＝E/2。因此带孔屏蔽腔的电场屏蔽效能为

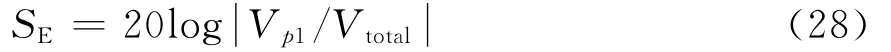
3.结果分析

3.1 屏蔽效能与频率的关系

图4给出了屏蔽效能随频率的变化关系。其中屏蔽空腔大小为300 mm×120 mm×300 mm（a×b×d），腔体壁上缝隙大小为50 mm×5 mm（l×w）。平面波以45°的角度入射，电场极化角Φ为30°。腔体壁由导电率为5.8×107S/m的铜构成，壁厚为1.5 mm.缝隙的中心位置坐标为X＝225 mm，Y＝60 mm.测试点P位于腔体中x＝225 mm，y＝60 mm，z＝140 mm的位置。

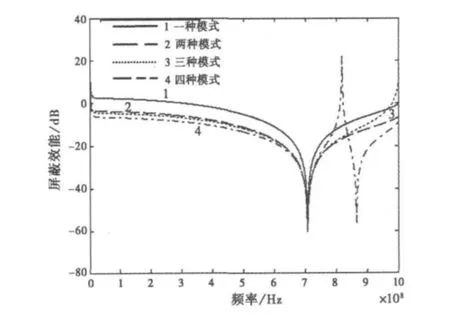
图4 考虑不同模式时屏蔽效能随频率的变化

3.2 屏蔽效能与入射角度的关系

图5给出了屏蔽效能与入射角θ的关系。腔体尺寸、材料、孔缝大小及位置、测试点位置与3.1相同。入射角θ在0°～90°之间变化，入射波频率为1 MHz.

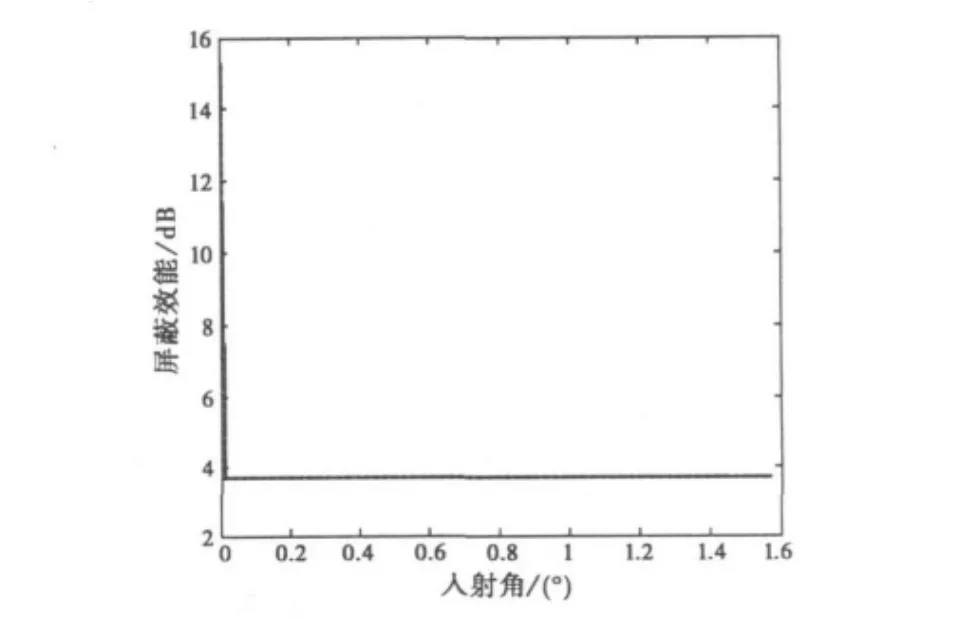
图5 屏蔽效能随入射角度的变化

3.3 屏蔽效能与距离的关系

图6显示了屏蔽效能与测试点位置的关系。测试点分别位于p1＝140 mm，p2＝180 mm 及p3＝270 mm的位置。其他设置与3.1相同。

4.讨 论

以上分析表明，根据文中给出的解析公式能够快速得到各个参量对腔体屏蔽效能的影响。

如图4曲线4所示，腔体在700 MHz和870 MHz发生了谐振。根据谐振频率计算公式

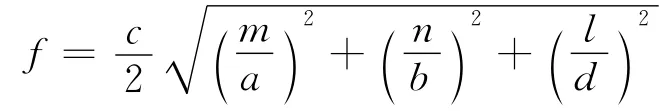
c为横电磁（TEM）波在空气中的传播速度，m、n和l代表腔体中的模式，则腔体内最低谐振频率近似为700 MHz，与本文得到的结果吻合，也与Robinson得到的结果相符[6]，在这些谐振频率上屏蔽效能变成负值。700 MHz为300 mm×120 mm×300 mm屏蔽腔中TE101模的谐振频率，870 MHz为高次模的谐振频率。由此可见，在分析有孔腔体屏蔽效能时，采用高次模分析是很有必要的。分析图4还可以得到，在高次模出现以前，低于谐振频点屏蔽效能随着频率的增加单调降低，高于谐振频点屏蔽效能随着频率的增加单调升高。

图5表明除了在零入射角附近，屏蔽效能与入射角关系不大。屏蔽衰减可以分解为吸收损耗和反射损耗。经分析，吸收损耗与入射角关系不大。而平行极化分量和垂直极化分量的反射损耗随着入射角的变化而变化，但两者随入射角变化的趋势相反，平行极化分量的反射损耗随入射角的增大而减小，而垂直极化分量的反射损耗随入射角的增大而增大，所以总反射损耗与角度相关性不大。

图6表明屏蔽效能随着离孔缝位置的增加而增加。腔体内离缝隙越远，屏蔽效能越好。因此可将敏感设备放在腔体内离缝隙较远的位置。

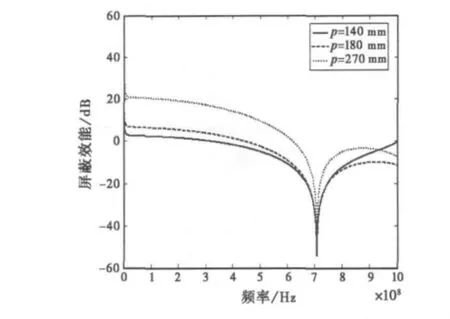
图6 屏蔽效能与测试点位置的关系

5.结 论

本文研究了缝隙偏离中心的有孔屏蔽腔屏蔽效能，得到的结果可用于分析任意极化斜入射平面波的情况。由于采用了高次模分析，因此解析结果适用于较高的工作频率。结果表明，在腔体谐振频率处，屏蔽效能出现负值，这是实际设计时尽量避免出现的情况，并且在谐振频率以下，离孔缝越近，耦合进入腔体的能量就越多，屏蔽效能越差。得到的解析公式还可用于分析孔缝位置和入射角角度对屏蔽效能的影响。综上所述，本文中根据高次模传输线法得到的解析公式具有一定的普适性，可用于高频情况，还能清楚分析各个参量与屏蔽效能的关系，对工程实践具有一定的指导性。

[1] KRAFT C H.Modeling leakage through finite apertures with TLM[C] //IEEE International Symposium on Electromagnetic compatibility，IL，1994：73－76.

[2] KUNZ K S，LUEBBERS R J.The Finite Difference Time Domain Method for Electromagnetics[M] .Orlando，FL：CRC，1993.

[3] LI Min，NUEBEL J，DREWNIAK J L.EMI from airflow aperture arrays in shielding enclosure－experments，FDTD，and MOM modeling[J] .IEEE Transactions on Electromagnetic Compatibility，2000，42（3）：265－275.

[4] CERRI G，LEO R D，PRIMIANI V M.Theoretical and experimental evaluation of the electromagnetic radiation from apertures in shielded enclosures[J] .IEEE Transitions on Electromagnetic Compatibility，1992，34（4）：423－432.

[5] BETHE H A.Theory of Diffraction by Small Holes[M] .2nd ed.New York：Phys.Rev.，1944.

[6] ROBINSON M P，BENSON T M，CHRISTOPOULOS C，et al.Analytical formulation for the shielding effectiveness of enclosures with apertures[J] .IEEE Trans.Electromagnet Compatibility，1998，40（3）：240－247.

[7] PO’AD F A，JENU M Z M，CHRISTOPOULOS C，et al.Analytical and experimental study of the shielding effectiveness of a metallic enclosure with off－centered apertures[C] //17th International Zurich Symposium on Electromagnetic Compatibility.Singapore，2006.

[8] PO’AD F A，JENU M Z M，CHRISTOPOULOS C，et al.Multimode consideration in the analysis of shiel－ding effectiveness of a metallic enclosure with off－centred apertures[C] //International RF and Microwave Conference.Malaysia，2006.

[9] BELOKOUR I，LOVETRI J，KASHYAP S.A higher－order mode transmission line model of the shielding effectiveness of enclosures with apertures[C] //IEEE International Symposium on EMC，2001.

[10] RENDER M C，MARVIN A C.A multiple mode equivalent transmission line model of crosstalk between conductors in shielded environments [J] .IEEE Trans.on Electromagn.Compat.，1995，37（3）：488－494.

[11] BELOKOUR I，LOVETRI J.A 2D－transmission line model for the EM field estimation inside enclosure with apetures[C] //IEEE International Symposium on Electromagnetic Compatibility，2002.

[12] 汪柳平，高攸纲.装有PCB有孔矩形腔屏蔽效能的传输线法分析[J] .电波科学学报，2008，23（4）：740－744.WANG Liuping，GAO Yougang.Analysis of shielding effectiveness of rectangular cavity of loaded PCB with aperture by transmission line method[J] .Chinese Journal of Radio Science，2008，23（4）：740－744.（in Chinese）

[13] 石 丹，沈远茂，高攸纲.有孔屏蔽腔的高次模分析[J] .电波科学学报，2009，24（3）：510－513.SHI Dan，SHEN Yuanmao，GAO Yougang.High order modes analysis on shielding effectiveness of enclosure with off center aperture[J] .Chinese Journal of Radio Science，2009，24（3）：510－513.（in Chinese）

[14] 汪柳平，高攸纲.有孔矩形腔的屏蔽效能及其对谐振抑制研究[J] .电波科学学报，2008，23（3）：560－564.WANG Liuping，GAO Yougang.Analysis of shielding effectiveness for rectangular cavity with apertures and resonance suppression[J] .Chinese Journal of Radio Science，2008，23（3）：560－564.（in Chinese）

[15] 焦其祥.电磁场与电磁波[M] .北京：科学出版社，2004：285－290.JIAO Qixiang.Electromagnetic Field and Electromagnetic Wave[M] .Beijing：Science Press，2004：285－290.（in Chinese）

[16] GUPTA K C，GARG R，BAHL I J.Microstrip Lines and Slotlines[M] .Norwood，MA：Artech House，1979.

[17] DAVID M P.Microwave Engineering[M] .New York：John Wiley ＆sons，2005.

[18] COLLIN R.Field Theory of Guided Waves[M] .New York：McGraw－Hill Book Company，1960.