基于逆绕射抛物方程法的辐射源定位技术研究

李德鑫 杨日杰 王鸿吉 蒋志忠

（1.海军航空工程学院电子信息工程系，山东 烟台264001；2.空军哈尔滨飞行仿真技术研究所，黑龙江 哈尔滨150001）

1.引 言

辐射源无源定位技术是电子战的一个重要组成部分，无论是传统的战略战术电子侦察，还是电子干扰，都离不开利用目标辐射源的信号或外辐射源的信号对目标进行定位。目前的无源定位系统采用的基本技术有到达角（AOA，Angle of Arrival）定位技术、到达时差（TDOA，Time Difference of Arrival）定位技术、到达频差（FDOA，Frequency Difference of Arrival）定位技术，以及联合定位技术等[1－2]。受环境因素影响，传统的定位算法对于复杂环境非合作辐射源信号的来波方向、传播时间、距离等参数的估计将会变得十分复杂。

抛物方程法是一种前向全波法，能够处理垂直与水平方向上介质非均匀分布的环境，可方便地用于分析地形起伏变化、地表电磁特性变化及传播空间媒质折射率变化等条件下的电波传播问题[3－4]。澳大利亚Spencer等人在此基础上提出了逆绕射抛物方程定位系统（IDPELS，Inverse Diffraction Parabolic Wave Equation Localization System），能够实现复杂环境下的辐射源定位，在实测中具有很好的收敛效果[5－6]。

传统的IDPELS没有考虑远距离、大范围的辐射源定位、误差椭圆、电磁剖面取值方法等问题，限制了该方法的实际应用。本文将在理想大气辐射源定位的基础上，对一个和两个辐射源在标准大气、地形遮蔽条件下的定位问题进行分析，对定位误差、数据点取值、误差椭圆的绘制等问题进行研究。

2.逆绕射抛物方程法

设电磁场时谐因子为e－ikx，标量ψ表示电磁场分量，k为真空中传播常数，n为折射指数，直角坐标系（x，y，z）下，假设ψ与y无关，即大气沿水平方向均匀分布，只随距离（x轴）和高度（z轴）变化，则水平极化波中只有Ey为非零电场分量（ψ（x，z）＝Ey（x，z）），垂直极化波中只有Hy为非零磁场分量（ψ（x，z）＝Hy（x，z））。电波传播过程中，ψ（x，z）满足以下二维标量波动方程。

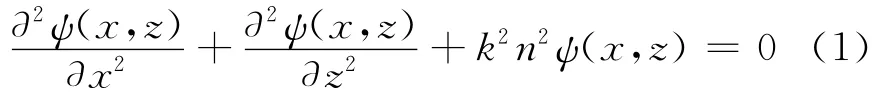
定义沿x轴正向传播的衰减函数为

将式（2）代入式（1），并作适当近似即可得到高度－距离空间的二维标量抛物方程，采用Feit－Fleck近似法[7]，得到 Feit－Fleck型抛物方程

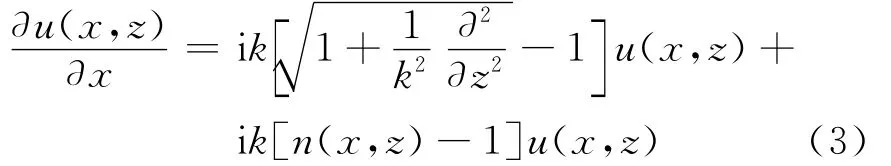
采用Leontovich边界条件[8]，视地海面为光滑理想边界。将 Cosine－taper（Tukey）窗函数[9]作为计算域的上边界，利用分步傅立叶变换（SSFT，Split－step Fourier transform）算法求解得

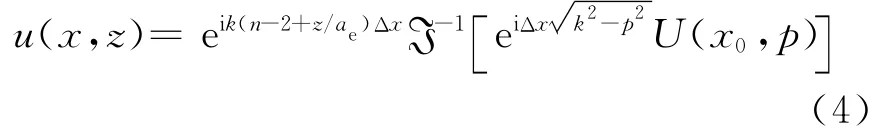
式中：ae为地球半径。定义反映路径上障碍物的绕射效应，N＝ eik（n－2＋z/ae）Δx反映传播媒介的折射效应，对于不规则地形条件N＝eik（n－2＋z/a＋z·∂2T/∂x2）Δx. e

抛物方程法是已知发射源初始场求解电波的空间分布；逆绕射抛物方程法与之相反，是由远场某一观测区域的场分布出发，求解电波的逆绕射问题，由于辐射源初始场是收敛的，从而可估计发射源的位置信息。电波在媒质中传播时，部分能量向空中辐射或被媒质和传播边界吸收导致损耗，且抛物方程是对椭圆型波动方程忽略后向传播的前向近似，因此无法对电波传播完全求逆。但是当边界条件已知时，该算法具有很好的收敛性。

对式（4）做逆函数推导可得电波传播的逆绕射抛物方程公式为

式（5）中的初始场u（x0，z）与式（4）中的不同，为远场截获的某一区域的场分布。

用逆绕射抛物方程模型计算水平极化条件下，电磁波在光滑海面上视距传播时的场分布特性。Leontovich边界条件中，海水介电常数εr＝80，海水导电率σ＝4 S/m；其它仿真条件，辐射源1高度z0＝300 m，电波频率f＝1 GHz，高斯方向图，天线增益35 dB，天线3 dB带宽为3.5°，观测距离为30 km.辐射源2高度z0＝100 m，电波频率f＝1.8 GHz，高斯方向图，天线增益29.5 dB，天线3 dB带宽为3°，观测距离为20 km.海面上为理想均匀大气n＝1。

图1（a）为辐射源1的逆绕射场强分布图，图1（b）为场强等高线图。图中u为折射脊线（主要由折射场分量叠加而成），v为反射脊线（主要由海面反射场分量叠加而成），A（x＝30000，z＝300.79）为场强极大值点亦为两条测向线的收敛点，即算法的估值点。由于算法步长（Δz≈1.6 m）的影响，对于高度z的估算产生了误差。由图1可以看出理想条件下算法具有很好的收敛性和估值精度。

图2为两个辐射源的场强分布图和等高线图，共有两个收敛点（20000，100.31），（29600，299.35）；由于两个辐射源相互干涉，对于辐射源1的距离估算产生了误差。由图2可以看出，对于两个辐射源的定位问题，算法仍具有很好的收敛性。

3.数据点的选取

选取观测位置垂直剖面上的一组场分布数据作为观测数据，在实际情况下，大范围数据点的获取需要大型天线和平台的大范围机动（如车载[5－6]或机载），并获取重点区域的电磁数据。数据点的取值范围及选取的位置会对定位造成误差，以标准大气条件下对辐射源1的定位为例，数据点的选取区域如图3所示，椭圆圈定的垂直剖面为观测数据，仿真实验数据点数由上下两边界向中点递减（图中标出了1024和512个数据点的取值区域），对于不同数据点情况下算法的估计值如表1所示。

数据点数为1024时，由于大气折射的影响，折射定位线给估值带来了误差，同时由于海面反射的干涉和叠加，使得对于高度z的估计有较大的误差。数据点数为512时，由于截取数据点距海面较远，受海面反射效应的影响减弱，对于z估计的精度提高；但由于精度较高的电波直线传播数据点数的减少，对于距离x的估计误差增加。中部数据点所含位置信息相类似，减少数据点数目对于估值并没有太大的影响，体现出算法具有很好的稳定性。算法的误差在32个数据点时开始急剧增加，小于16点时，算法失效。数据点的选取与辐射源的高度和观测距离有关，随着观测距离的增加受海面反射影响逐步减弱，但同时数据点所含位置信息也在减少。

表1 单个辐射源不同数据点数的估计值

两个辐射源定位的数据点选取情况与单个辐射源定位时相类似，不同之处在于，两个辐射源之间的干涉和叠加会对彼此的定位造成误差。辐射场范围较小的辐射源由于完全包含在大范围辐射源的辐射场中，受干涉影响其误差相对较大。对于辐射场范围较大的辐射源，选取干涉临界点以上的数据点会提高其定位精度，但同时会降低辐射场范围较小的辐射源定位精度。两个辐射源数据点选取与辐射源的高度、电波传播仰角、观测距离有关。需要指出的是，算法仅能解决不相干辐射源的多点定位问题，对于相干辐射源，由于辐射场之间相互干扰，导致算法失效。

对于大气折射的特殊情况——大气波导，由于其形成具有区域性、不均匀和不确定性，对于非合作辐射源的定位，很难估算大范围波导的真实折射和陷获情况。常见的大气波导陷获角一般很小，电波异常传播的区域一般局限在贴海面较低区域，为获取较高精度的估值，应尽量选取远离波导区域的数据点。

因此，关于数据点的选取，应选择尽量远离海面反射的较高区域，同时尽可能多的获得位置信息含量高的数据点，以提高定位精度。

4.误差椭圆

对于定位误差，可利用误差椭圆来说明定位区域和收敛范围。图4中，定义u为折射脊线，v为反射脊线，A为辐射源真值点，O为估算的收敛点，θ为u、v的交角，γ为v、x的交角，E1、E2为测向线误差。

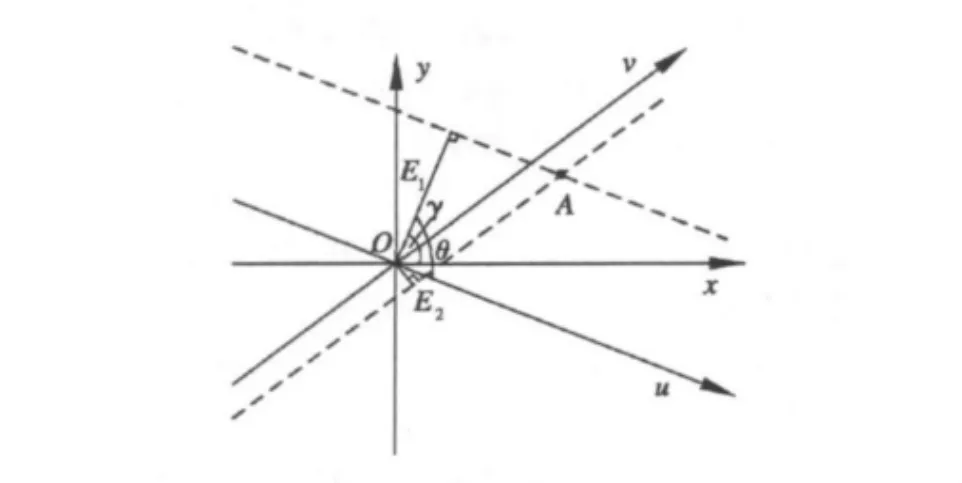
图4 定位误差分析

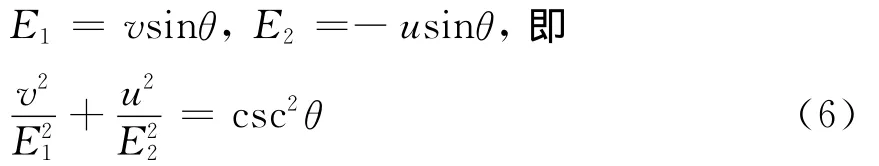
式（6）为uOv坐标系下的椭圆，与xOy坐标系的变换公式为

其中：

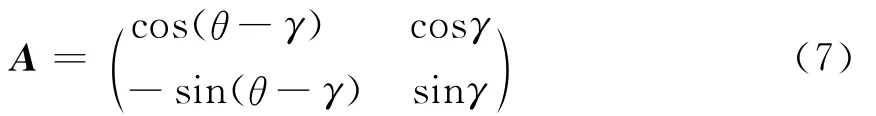
将式（7）代入式（6）即可获得直角坐标系下的误差椭圆公式。

对于地球表面大气条件下的辐射源定位问题，按照国际电讯联盟（ITU－R）[10]规定的对流层标准大气条件∂n/∂h≈－40×10－6计算折射指数n，对单个辐射源和两个辐射源的定位情况进行仿真，其余仿真条件与理想大气情况相同。绘制定位区域场强等高线图，图5为表1中512个数据点情况；图6为两个辐射源1024个数据点情况；图7为两个辐射源选取靠近上边界的512个数据点情况（注意与图5取值区域不同）。

图5～6中“＊”为算法的估值点，“Δ”为辐射源真实位置，由两图可以看出，误差椭圆随着估计误差的增大面积随之增大，能够反映出收敛域的面积、方向等信息，很好地说明了估值点与真值点的关系，直观显示出算法的收敛区域和定位精度。

需要说明的是，图5～7绘制的是场强等高线图，由于折射、反射叠加效应的影响，折射脊线与反射脊线不再是图1中理想情况下的等高线，而是一条收敛带中各区域场强极大值叠加而成的收敛线（由于各极值不相等，故不再是一条等高线），三维图可以很好地显示出这种收敛的趋势。

如前文所述，由于两个辐射源间的相互干涉和叠加，对各自的定位估值带来了较大的误差。图5与图6中关于辐射源1的定位估值点分别为（29500，296.16）和（29400，278.65），相应的误差椭圆面积与方向有所不同，误差椭圆面积随误差增加而增大，椭圆的倾角说明定位值的误差朝向；图6辐射源2的定位值为（19900，85.98），该辐射源的辐射区域完全被辐射源1覆盖，由反射折射叠加带来的误差较大，验证了前文的论述。

图7为两个辐射源512个数据点时的定位情况，其余仿真条件与图6相同，此处的数据点由于选取上部的512个点，剔除了受海面反射影响较为强烈的下部数据点。因此，定位线收敛性强，定位效果较好。两个辐射源的定位值分别为（29400，283.43），（19600，101.91），与图6的定位值相比，高度估值精度有较大提高；但是由于剔除掉了部分携有反射距离信息的数据点，受折射效应的影响，距离误差有所增加。两个辐射源相互间的干涉影响主要体现在海面反射效应上，上述仿真实验中，辐射源2高度较低，观测数据中由于海面反射效应的混叠导致误差增加，因而定位误差增大。

5.地形遮蔽条件下的辐射源定位

对流层电波传播中，不规则地形是影响电波传播特性的另一主要因素，可利用类似正弦包络形状的不规则地形分析地形遮蔽对定位算法的影响。地形模型为

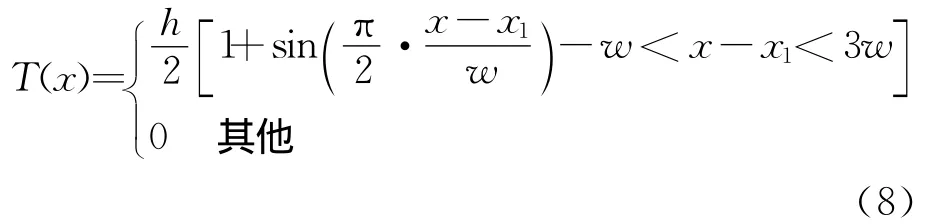
式中：h为包络的最大高度；x1为包络半高程所在的距离；w为包络的半宽度。仿真设定值，地形1为h＝600 m，x1＝20000 m，w＝1000 m；地形2为h＝200 m，x1＝10000 m，w＝1000 m（此处设定值是相对于观测区域而定）。

标准大气条件下，受地形遮蔽影响的两个辐射源辐射场分布如图8所示，此处为地形1，其它仿真条件与图6相同。利用逆绕射抛物方程法的场分布图如图9所示。

依前例，“＊”为算法的估值点，“Δ”为辐射源真实位置；由图9可以看出，在地形遮蔽条件下，算法仍有很好的收敛性。图10中，受地形遮蔽影响，下部分观测值的信息损失很大，对于辐射源1的定位值为（29400，277.06），与图6的精度相当，辐射源2的位置信息损失过大，无法定位。

辐射源定位精度与地形最大高度有关，一般情况下当山峰的高度高于辐射源天线3 dB带宽角所能达到的最大视距高度时，定位精度将会急剧变差，直至算法失效。图9中，山峰的高度高于3 d B带宽角所能达到的最大视距高度，低于电波传播的最大仰角视距高度，定位失效。

图10为图9的等高线场分布图，两图山峰位置处均有一个明显的劈尖，利用该劈尖信息可以估算地形的最大高度。因此，当辐射源位置已知情况下，该算法还可应用于地形的估算。

图11为地形2条件下的局部等高线场分布图，两个辐射源的定位值分别为（29600，277.06）和（19900，82.80），由定位误差椭圆可以看出，算法在较低山峰遮盖下的定位精度与标准大气条件下相当，体现了算法的稳定性和实用性。

6.结 论

在理想大气辐射源定位的基础上，对一个和两个辐射源在标准大气、地形遮蔽条件下的定位问题进行了分析，研究了定位误差、数据点取值、误差椭圆绘制等问题，提高了算法的定位精度，扩大了算法的应用范围。

逆绕射抛物方程法可对远距离、大范围复杂条件下的电波传播进行预测，对非合作辐射源进行定位，对未知地形进行估算，具有很好的应用前景。

逆绕射抛物方程法有着自身的缺陷，需要观测大范围的场强数据来保证估值的精度，进而需要大型天线和平台的大范围机动来保障。算法的收敛性与计算步长有关，步长越小估值精度越高，但是算法的复杂度随之增加，计算时间增大，实时性变差。

后续的工作应当包括数据点选取建模、误差概率统计及动态海面、杂波、复杂地形条件下的建模，以期在最佳高度、距离观测最少的数据点获得较高的定位精度，提高算法的适用性和稳定性。

[1] 曹轶超，方建安，罗贤云.一个基于TDOA的无线定位新算法[J] .电波科学学报，2008，23（5）：841－846.CAO Yichao，FANG Jianan，LUO Xianyun.Constrained least－squares and wireless location based on TDOA measurements[J] .Chinese Journal of Radio Science，2008，23（5）：841－846.（in Chinese）

[2] 王 强，钟丹星，邓新蒲，等.基于圆锥向角和相位差变化率的运动单平台无源定位算法和精度分析[J] .航空学报，2009，30（8）：1497－1502.WANG Qiang，ZHONG Danxing，DENG Xinpu，et al.Single moving observer passive localization algorithm using conical bearings and rate of phase difference change and its accuracy analysis[J] .Acta Aeronautica et Astronautica Sinica，2009，30（8）：1497－1502.（in Chinese）

[3] 胡绘斌，毛钧杰，柴舜连.电波传播中求解宽角抛物方程的误差分析[J] .电波科学学报，2006，21（2）：199－203.HU Huibin，MAO Junjie，CHAI Shunlian.Error analysis of wide－angle parabolic equation for radio propagation[J] .Chinese Journal of Radio Science，2006，21（2）：199－203.（in Chinese）

[4] 姚景顺，杨世兴.抛物方程模型在海上电波传播中的应用[J] .电波科学学报，2009，24（3）：493－497.YAO Jingshun，YANG Shixing.A terrain parabolic equation model for propagation over the ocean[J] .Chinese Journal of Radio Science，2009，24（3）：493－497.（in Chinese）

[5] SPENCER T A，WALKER R A，HAWKES R M.Inverse diffraction parabolic wave equation localization system （IDPELS）[C] //International Symposium on GNSS/GPS.Sydney，Australia，2004：1－15.

[6] SPENCER T A，WALKER R A，HAWKES R M.Inverse diffraction parabolic wave equation localization system （IDPELS）[J] .Journal of Global Positioning Systems，2005，4（1－2）：245－257.

[7] FEIT M D，FLECK J A.Light propagation in graded index fibers[J] .Appl Opt，1978，17（24）：3990－3998.

[8] KUTTER R，DOCKEY G.Theoretical description of parabolic approximation Fourier split－step method of representing electromagnetic propagation in the troposphere[J] .Radio Science，1991，26（2）：381－393.

[9] HARRIS F J.On the use of windows for harmonic analysis with the discrete Fourier transform[J] .IEEE Proc，1978，66（1）：51－83.

[10] 熊 皓.无线电波传播[M] .北京：电子工业出版社，2000：361－375.