多数据源电离层层析成像方法
2011-08-08赵海生许正文
赵海生 许正文
(1.中国电波传播研究所,电波环境特性及模化技术重点实验室,山东 青岛266107;82.中国科学院空间天气学国家重点实验室,北京100190)
1.引 言
电离层层析成像(简称CIT)已成为一种重要的电离层探测手段,地面接收站通过接收卫星信标信号,根据信号的差分相位、时延、法拉第旋转等,提取从卫星信标到地面接收站之间的电子密度总含量(TEC)。根据地面站测得的不同星地连线的斜向TEC,进行反演区域的电离层CIT成像。电离层CIT成像技术从提出至今已有20多年的历史,众多学者提出各种各样的CIT算法[1-4],但直到现在仍没有彻底解决电离层CIT技术的有限视角、稀疏布站等不适定性问题。因此,CIT成像结果的精度仍然不高,从而影响了电离层CIT技术的广泛应用。
大地震前存在电离层异常扰动的观点已逐渐被认可,从1964年发现地震与电离层存在某些联系,至今已有许多设备观测到了震前电离层异常扰动[5-11]。但是地震与电离层扰动存在不对应性,很多时候电离层出现异常扰动并没有地震发生。地震和电离层扰动的不对应性,是试图通过观测电离层异常变化来预报地震的学者首先要解决的难题。为了减轻地震对我国人民生命财产造成的重大损失,也为了解决这一难题,我国启动了电磁卫星计划,其目标是力争到2020年,初步形成高低轨道优化配置、稳定在轨运行的地震电磁卫星星座,从而使空间技术与地面观测台网结合起来,实施地震立体观测,获取更加全面系统的观测信息,推动防震减灾能力的提高。
要从众多的电离层扰动中,精确提取地震信息,就要深入研究地震引起电离层扰动的特点。比如,地震扰动的强度、高度、形状、持续时间等可能与其他原因引起的电离层扰动存在差异,因此,只有深入了解了地震扰动的特征才能将它精确识别。我国决定在地震电磁试验卫星上携带三频信标发射机,试图通过电离层CIT成像技术,进行地震扰动特征的提取。然而目前CIT技术的现状,并不具备高精度CIT成像的能力,在地震扰动特征提取上存在很大难度。多年的实践经验表明:单靠CIT算法的改进,无法彻底解决有限视角、稀疏布站等问题,无法从根本上提高CIT成像精度。许多学者将目光转向多数据源融合方法,试图从另一途径解决CIT技术面临的问题,其中有学者提出全球定位系统(GPS)数据和地基垂测仪数据联合CIT成像的方法[12],还有人提出三频信标数据和我国华北地震监测网垂测、斜测数据联合反演的方法[13],这些方法一定程度上提高了反演精度,但没有彻底摆脱模型对CIT技术的制约,初值往往依靠模型生成,初值若与实际吻合得好反演结果精度高,反之精度下降。本文提出的融合地面垂测、斜测数据、顶部探测仪数据和三频卫星信标数据的多数据源电离层联合CIT方法,从根本上摆脱了模型的限制,初值由地面垂测、斜测数据和顶部探测仪数据生成,因此,该方法能够获得稳定的高精度反演结果。模拟结果证明了该方法的可行性。
2.多种数据资源
2.1 地基高分辨率电离层监测网
研究发现,地震前兆的电离层异常特征尺度在百千米量级,具体尺度的大小因震级大小等因素而异。而我国现有的电波环境观测网站之间相距至少600千米以上,难以有效开展电离层中小尺度不均匀性结构的观测与研究。因此,通过建设电离层地基高分辨率观测网,实现百千米尺度的电离层监测,对于开展电离层不均匀性研究,用于地震前兆研究,有着明显的应用背景。
我国的首个电离层地基高分辨率观测网于2009年4月建成并投入观测,采用电离层斜向探测技术,依托中国电波传播研究所已建的北京、长春、青岛、新乡、苏州5个垂直探测站,在中国地震局的首都圈地震监测台站布设20台电离层斜向探测仪,每个斜测站同时接收5个垂测站的信号,链路反射点总共可形成100个电离层监测点,链路大圆距离均在2000 km以内,其中600 km以内的斜测链路达50条。经计算,按照100 km的空间分辨率,各链路的反射点基本可以覆盖整个华北地区。垂测站、斜测站分布图如图1所示。
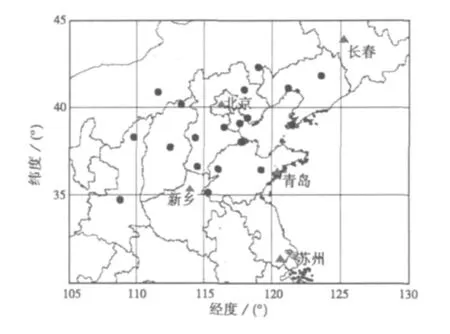
图1 电离层地基高分辨率观测网分布图
2.2 电子密度剖面反演方法
电子密度剖面就是电子密度随高度的变化,它是电离层探测所获得的最有意义的结果之一。由某高度的反射频率可以精确计算该高度的电子密度
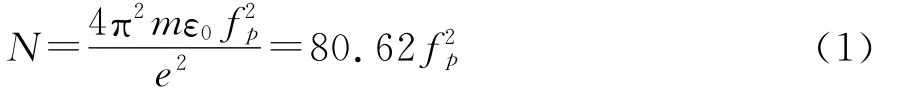
式中:N为电子密度;m为电子质量;ε0为自由空间介电常数;e为电子电荷量;fp为等离子体频率。
电离层图上每个描迹对应的高度并不是该点的实际高度,该高度称为虚高,虚高和实高的对应关系式为

式中:h′(f)为虚高;μ′为群折射指数;h0为电离层底高;fp为等离子体频率;h为实高。推算电子密度剖面关键是计算每个反射频率对应的反射高度。反射高度的精确计算至今还是一个难题[14-17],目前广泛应用的解算电子密度剖面的方法是 “分片法”,算法的具体推导过程参考文献[18] 。
2.3 三频信标TEC测量方法
三频信标与双频信标相比多了一个载波ω3=ω0,将三个频率载波两两差分可以得到三组双频载波,三组载波利用差分多普勒技术可以得到三个差分相位表达式
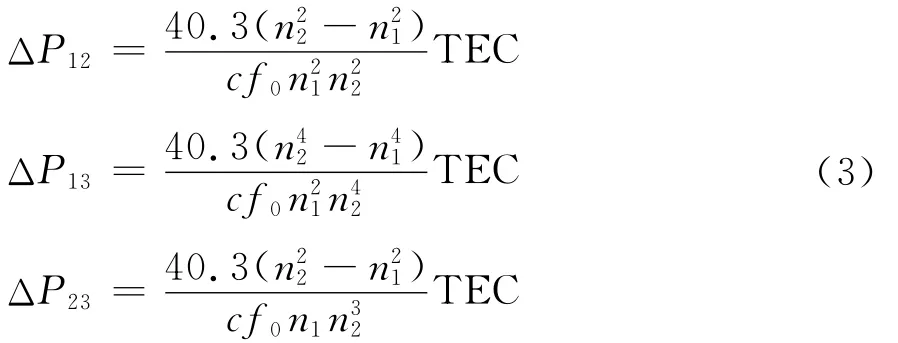
式中:ΔP12、ΔP13、ΔP23为差分相位的绝对值,包含相对相位和相位积分常数。经推导、整理可得(推导过程详见文献 [19] )

式中:Δφ12、Δφ13分别为f1与f2,f1与f3的差分相位的小数部分。在三频卫星信标中n1=3,n2=8,f0=16.668 MHz,将其带入式(4)得

式中:8.3165×1016(单位为el/m2)称为三频信标测量TEC的相位模糊系数;k2为一正整数,它与双频信标的相位积分常数一样,是需要确定的,把k2称为三频相位积分常数。文献[19] 给出了k2的计算方法。
3.数据融合方法
从我国首都圈地震监测网选取8个站点(如表1),其中包括4个垂测站和4个斜测站,各个站反射点分布如表1所示。携带顶部探测仪的地震电磁卫星沿120°E经度飞行,在每个反射点及27°N和48°N上空完成一次扫频,分别得到一张顶部电离图,反演得到顶部电子密度剖面。同一时刻的顶部探测数据和底部探测数据联合,经过数据融合处理可得到整个反演区域二维电子密度剖面,我们以此作为迭代初值进行了CIT成像研究。具体数据融合算法如下:

表1 选取的垂测站点及反射点位置
1)由顶部探测仪得到8个反射点和27°N、48°N上空顶部电子密度剖面。
2)由垂测仪得到底部电子密度剖面,由斜测仪得到反射点底部2~3个关键点的电子密度数据。
3)由4个垂测仪得到的底部电子密度剖面与同一时刻同一纬度位置的顶部电子密度剖面结合,得到4个完整电子密度剖面。
4)4个斜测反射点,底部数据由Chapman模型拟合得到,拟合过程中通过调整参数,使模型以最小二乘原理与斜测数据吻合;顶部数据由顶部探测仪数据得到。
5)在27°N、48°N处底部数据完全由Chapman模型得到,顶部数据由顶部探测仪数据得到。
6)对以上方法得到的10个电子密度剖面分别进行滤波平滑处理,然后用二维插值函数拟合出0.5°分辨率的完整的二维电子密度剖面。
由于站点分布稀疏、数据拟合误差等原因,经过数据融合处理的二维电子密度剖面存在不可避免的误差。但是该电子密度剖面以实测数据为基础,完全克服了模型的限制,以此作为迭代初值与以模型作为初值相比,更具有稳定性和可靠性,从而提高了CIT成像结果的精度。
4.数值模拟
为了验证算法的有效性,我们采用乘法代数算法(MART)进行电离层CIT反演,根据我国首都圈地震监测网的布站情况,采用沿120°E经线,30°N~45°N区域作为反演区域,选取8个地面站点(表1)。为了检验算法对小尺度扰动的监测能力,我们在34°N~38°N和40°N~42°N附近分别加入一个水平尺度约400 km和200 km的电离层扰动。再结合卫星信标的具体情况设置试验参数如下:
时间:2009年11月17日世界时6时;
反演区域高度范围:100~500 km;
卫星纬度跨越:27°N~48°N;
反演区域纬度跨越:30°N~45°N;
台站设置:沿120°E,在33°N~43°N之间,每2个纬度一个台站;
经度:120°E;
网格划分:每个网格垂直10 km,纬度跨越0.5°;
地面站选取:如表1;
TEC采样间隔:约0.064°(每隔0.064°一次TEC采样);
迭代初值:20091017UT0600和20090517UT0600时刻IRI2007模型算得的电子密度分布。
由于我国地震电磁试验卫星尚未发射,目前无法得到实测的三频信标TEC数据和顶部探测数据,检验该算法的数据只能通过模型得到。为了使模拟结果更符合实际,我们在数值模拟中加入了适当的随机误差。反演结果和误差比较如图2和图3所示。
从图2、图3可以看出采用本文算法,基于多数据融合,利用实测数据生成迭代初值的反演结果明显优于由模型生成的迭代初值的反演结果,20091017UT0600时刻的IRI模型作为初值的反演误差为:1.2367×1011el/m3,20090517UT0600时刻的IRI模型作为初值的反演误差为:1.4689×1011el/m3,而由实测数据生成的迭代初值反演误差仅1.3809×1010el/m3.另外,在水平尺度为200 km的小尺度扰动的监测方面,本文算法对小尺度扰动形状、尺度的反演更接近模型,明显优于另外两个反演结果。
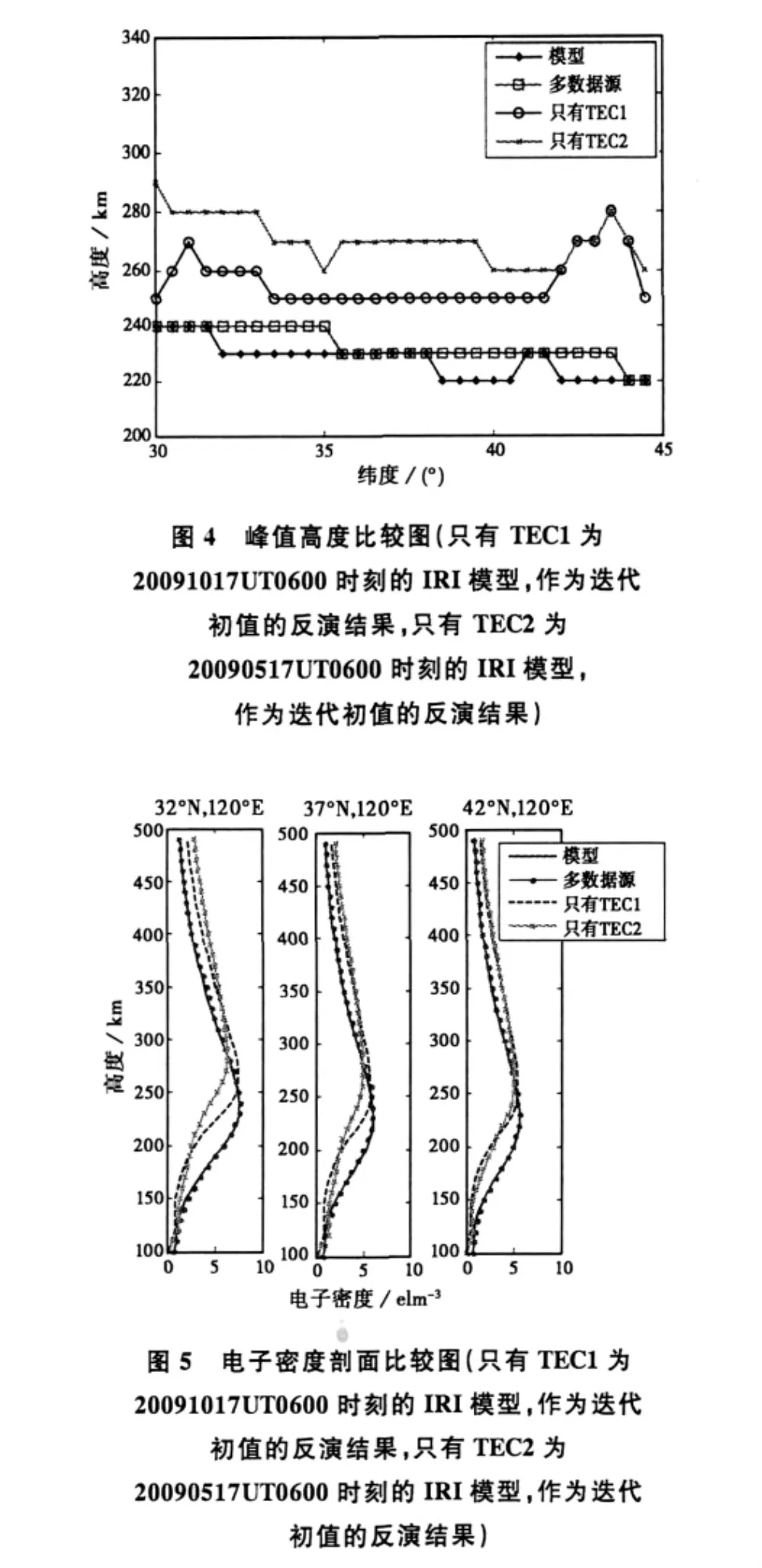
图4、图5进一步给出了反演结果的峰值高度比较和在32°N、37°N和42°N三个纬度点电子密度剖面比较(图5横坐标的单位为1×1011el/m3)。从两图能够清晰看出本文算法在提高反演结果垂直分辨率方面的效果,这一方法有效弥补了CIT成像有限视角的不足。
5.结 论
垂直分辨率不高是电离层CIT技术面临的一个重要问题,结合三频信标技术、地基高分辨率地震监测网及顶部探测技术,提出了一种实用有效的联合CIT算法,并利用IRI模型对算法进行了检验,结果表明:采用本文提出的算法,能够提高CIT反演精度,有效弥补有限视角不足。本算法将顶部探测技术应用于电离层CIT成像研究,进一步增加了数据源的类型,提高了反演精度,是本算法创新之处,也为我国地震电磁卫星电离层扰动探测提供了一种新的算法。
[1] RAYMUND T D,AUSTEN J R,FRANKE S J,et al.Application of computerized tomography to the investigation of ionospheric structures[J] .Radio Sci.,1990,25(5):771-789.
[2] FREMOUW F J,SECAN J A,HOWE B M.Application of stochastic inverse theory to ionospheric tomography[J] .Radio Sci.,1992,27(5):721-732.
[3] KUNITAKE M,OHTAKA K,MARUYAMA T,et al.Tomographic imaging of the ionosphere over Japan by the modified truncated SVD method[J] .Ann.Geophys.,1995,13(12):1303-1310.
[4] FRIDMAN S V,L NICKISCH J,HAUSMAN M.Personal-computer-based system for real-time reconstruction of the three-dimensional ionosphere using data from diverse sources[J] .Radio Sci.,2009,44(3):RS3008.doi:10.1029/2008RS004040.
[5] PULINETS S A.Strong earthquakes prediction possibility with the help of topside sounding from satellites[J] .Adv.Space Res.,1988,21(3),455-458.
[6] LIU J Y,CHEN Y I,PULINETS S A,et al.Seismoionospheric signatures prior to M 6 Taiwan earthquakes[J] .Geophys.Res.Lett.,2000,27(19):3113-3116.
[7] SILINA A S,LIPEROVSKAYA E V,LIPEROVSKY V A,et al.Ionospheric phenomena before strong earthquakes[J] .Nat.Hazards Earth Syst.Sci.,2001,1(3):113-118.
[8] PULINETS S A,BOYARCHUK K.Ionospheric Precursors of Earthquakes [M] . Berlin Heidelbert:Springer-Verlag,2004.
[9] PARROT M,BERTHELIER J J,LEBRETON J P,et al.Examples of unusual ionospheric observations made by the DEMETER satellite over seismic regions[J] .Phys.Chem.Earth,2006,31(4-9):486-495.
[10] ZHAO B,WANG M,YU T,et al.Is an unusual large enhancement of ionospheric electron density linked with the 2008 great Wenchuan earthquake?[J] .J.Geophys.Res.,2008,113:A11304.doi:10.1029/2008JA013613.
[11] LIU J Y,CHEN Y I,CHEN C H,et al.Seismoionospheric GPS total electron content anomalies observed before the 12 May 2008 Mw7.9 Wenchuan earthquake[J] .J.Geophys.Res.,2009,114:A04320.doi:10.1029/2008JA013698.
[12] MA X F,MARUYAMA T.Three-dimensional ionospheric tomography using observation data of GPS ground receivers and ionosonde by neural network[J] .J.Geophys.Res.,2005,110:A05308.doi:10.1029/2004JA010797.
[13] ZHAO H S,XU Z W,WU J,et al.Ionospheric tomography by combining vertical and oblique ionograms with TEC retrieved from a tri-band beacon[J] .J.Geophys.Res.,2010,115:A10303.doi:10.1029/2010JA015285.
[14] DAVIES K.Ionospheric Radio[M] .London:Peter Peregrinus,1990.
[15] OBROU O K,BILITZA D,ADENIYI J O,et al.E-quatorial F2 layer peak height and correlation with vertical ion drift and M(3000)F2[J] .Adv.Space Res.,2003,31(3):513-520.
[16] RAWER K and EYFRIG R.Improving the M(3000)-hmF2 relation[J] .Adv.Space Res.,2004,33(6):878-879.
[17] XU Z W,WU J,IGARASHI K,et al.Long-term ionospheric trends based on ground-based ionosonde observations at Kokubunji,Japan[J] .J.Geophys.Res., 2004, 109: A09307. doi:10.1029/2004JA010572.
[18] 熊年禄,唐存琛,李行健.电离层物理概论[M] .武汉:武汉大学出版社,1999.
[19] ZHAO H S,XU Z W,J WU,et al.Ionospheric tomography of small-scale disturbances with a triband beacon:a numerical study[J] .Radio Sci.,2010,45:RS3008.doi:10.1029/2009RS004247.
