障碍物对蒸发波导中电波传播影响研究

李广成 郭立新 吴振森 刘金海

（西安电子科技大学理学院，陕西 西安710071）

1.引 言

大气波导是由于大气折射条件引起的一种异常大气结构。当传播的电磁波满足一定的陷获频率和陷获角后，大气波导能够陷获部分电磁波使其在波导层内形成超视距电波传播，同时也会形成雷达探测盲区以及增强雷达海杂波[1－3]，因此，大气波导的存在对海上运作的雷达和通讯设备等无线电系统影响很大。蒸发波导是大气波导中的一种最典型和常见的波导形式，蒸发波导普遍存在于近海面上空，统计表明，蒸发波导高度一般在海面上方40 m以下，其影响的电磁波频率一般在30 MHz以上，陷获角一般不大于0.4°，最大可达0.8°[2]。近年来，随着各类近似、数值算法及计算机计算速度的提高，国内外学者对蒸发波导的研究越来越加深入，主要的模型有射线跟踪模型、波导模型、抛物方程法（PE）模型等以及各种模型的混合法[4－5]。

抛物方程法最早由FOCK提出，是一种前向全波分析法，抛物方程法从波动方程出发忽略电波的后向传播或散射的影响，从而把波动方程简化成关于传播方向为一阶微分的抛物型方程，抛物方程法能处理垂直与水平方向上介质非均匀分布的环境，由于其计算准确、计算稳定等优点，在对流层电波传播中得到了广泛的运用。抛物方程方法分为窄角抛物方程法（NAPE）和宽角抛物方程法（WAPE），最初人们主要应用窄角抛物方程法求解电磁波在大气波导中以及低掠射角情况下的传播，小掠射角时比较准确，而海上蒸发波导往往发生在距海面高度为30 m的范围内，因此，当电磁波在波导中传播的过程中很容易遇到岛屿、舰船等障碍物，此时，窄角抛物方程法已经不能准确地预测复杂海面情况下的电波传播，为了能够更准确地预报波导对电磁波的影响，需要寻求一种更合理的解法，以便能更准确的计算和预测。为了能够更准确地建立电磁波在大掠射角情况下的抛物方程模型，人们提出了宽角抛物方程法、Beilis－Tappert平移变换法[6－8]以及分段线性平移变换法[9]等。宽角抛物方程能够处理简单的地形对电磁波传播的影响，却在处理复杂地形时有一定的局限性、Beilis－Tappert平移变换法改进了宽角抛物方程处理复杂地形时准确度低的缺陷，但是必须知道地形及障碍物的曲率，而在许多实际运用中地形曲率却难以求解。分段线性平移变换法不仅避免了以上两方法的缺陷，而且能够通过傅里叶变换准确地处理复杂地形情况下的电磁波的传播。本文将利用分段线性平移变换法来研究海面上方简单类型的障碍物对蒸发波导中电磁波传输特性的影响。

2.分段线性宽角抛物型方程方法

抛物方程模型包括窄角抛物方程和宽角抛物方程。窄角抛物方程适用于掠入射角小于15°，但对于更大的掠入射角，用窄角抛物方程计算误差太大，必须采用宽角抛物方程。通常在一般的传播条件下，宽角抛物方程能够较好地处理掠入射角大于15°时的海面上方简单形状障碍物的情形，但是，当海面上方岛屿的地形高低起伏变化相当快时，由于受到步长Δx取值的限制（当步长Δx取值太大时，可能会造成看不到障碍物的情形，以至于在障碍物后方一段距离内的场强估计不准确，而取值太小会影响到计算速度），当步长Δx较大时，可能会给计算结果造成较大的误差。

以下是一种经典的处理不规则地形及障碍物的模型，由Beilis A和Tappert FD提出[6]，对于这样含地形或障碍物的情况，需要通过坐标变换法求解抛物方程（如图1所示）。

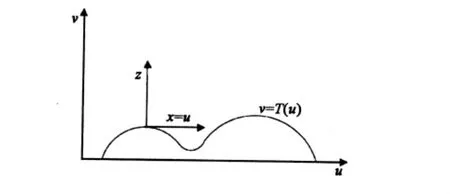
图1 不规则地形的坐标变换示意图

图1中u，ν是与坐标轴相对应的横坐标和纵坐标，令x＝u，z＝ν－T（u），则可将不规则地形坐标变换到直角坐标x－z坐标系下。通过坐标变换后再求解抛物方程，求解方法分为Beilis－Tappert平移变换法和分段线性平移变换法。Beilis－Tappert平移变换法虽然在处理复杂形状的地形及障碍物时能够取得很好的结果，但是主要缺点是必须知道地形及障碍物的曲率T″，而在许多实际运用中地形曲率却难以求解，因此，模型的精确度不高。为了能够解决复杂地形或障碍物上曲率难于求解以及精度不高的问题，Donohue D J和Kuttler J R在对Beilis－Tappert平移变换法改进的基础上提出分段线性平移变换法。和前面两个模型相比，它有两个最大优点：一是分段线性变换模型符合宽角抛物方程模型用于处理复杂地形电波传播求解问题，并且解决了复杂地形曲率难以求解电波波导传播的问题；二是这种模型可以精确地反映地形的起伏对地表边界阻抗特性的影响。因此，本文选择分段线性平移变换法[9]作为处理海面上方地形及障碍物的方法和依据。

由 Helmholtz方程可知[9]

式中：k＝2π/λ；φ（u，ν），n分别是对应的矢量场，波束和介质的相对折射率；u，v是与坐标轴相对应的横坐标和纵坐标。

令x＝u，z＝ν－T（u），利用坐标变换，有

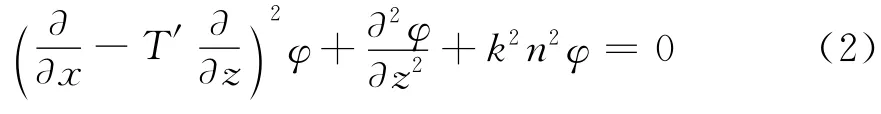
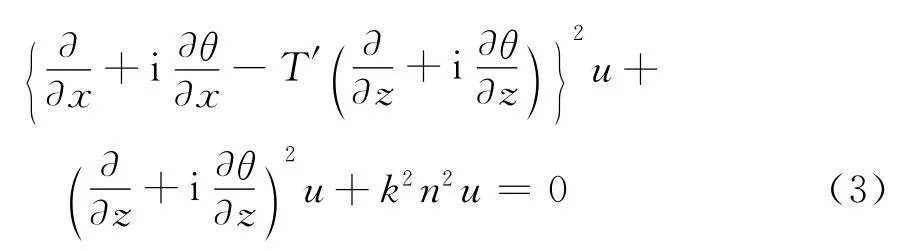
将式（3）因式分解为

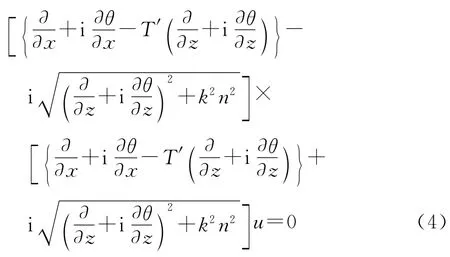
式（4）等号左边两乘积分式分别代表前向传播和后向传播的电磁波。为了便于求解，忽略电磁波后向传播的影响，取前向传播因式为

若为平坦地形（T′＝0，θ＝0），式（5）可化为

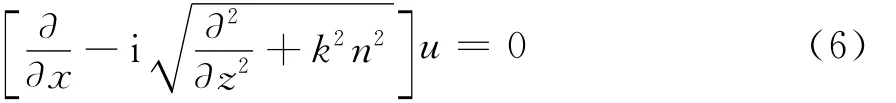
式（6）就是标准的宽角抛物型方程。

复杂地形情况下，将式（5）进行一系列复杂的变换求解过程，可得到如下地形宽角抛物方程形式[9]

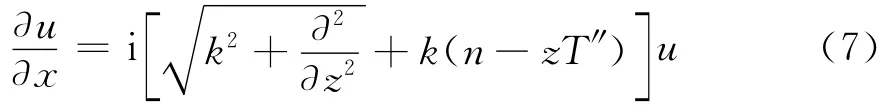
直接对方程（7）中的x求积分，则x＋Δx处的场用x可表示为

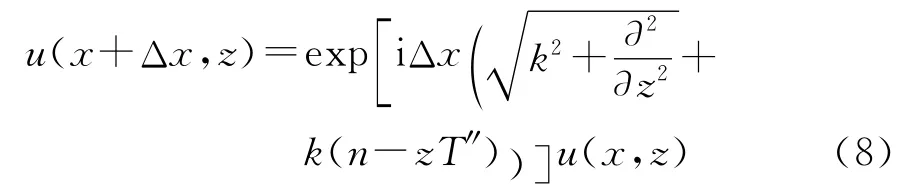
利用标准的傅立叶变换方法对式（7）中z变量积分，定义U（x，p）是u（x，z）的傅立叶变换，即

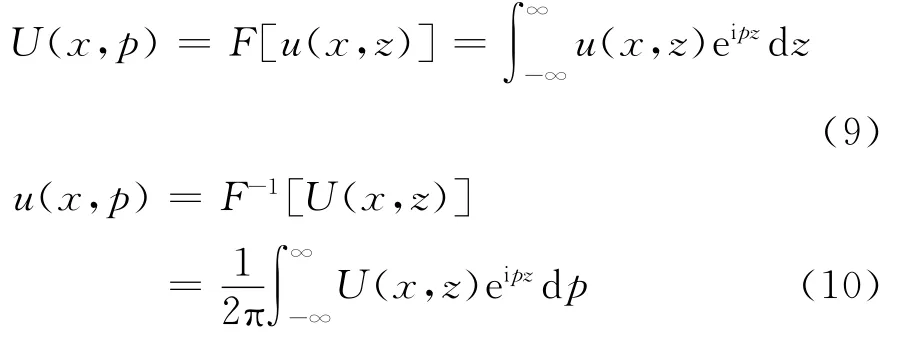
利用式（8），（9），（10），可得宽角抛物方程的解为

式中：m（x，z）＝n（x，z）－z·T″；p是垂直空间波数，令p＝k sinθ，θ为天线仰角；Δx为x方向步长。式（11）在x方向上以Δx为步长步进，对于给定的快速傅立叶变换（FFT）范围，Nyguist定理要求的离散步长限定了z空间的最大高度zmax和p空间最大角度θmax，且满足zmaxpmax＝Nπ，由式（11）可得到在某一特定距离处所有高度上的场强分布，先对某一距离上的场强做傅里叶变换，乘以平方指数项，再做逆傅里叶变换，再乘以另一指数项，可得到下一递增步长处的场强，如此重复计算便可以算出电磁场在水平传播方向上的场强。

当电磁波传播经过有拐点的地形或者障碍物时，由于斜率T发生较大的变化，造成相位θ的不连续性。如果地形为分段线性地形（如图2），则需要对电磁场进行相应的修正，若地形为连续性地形（如图3），则不需要进行修正。

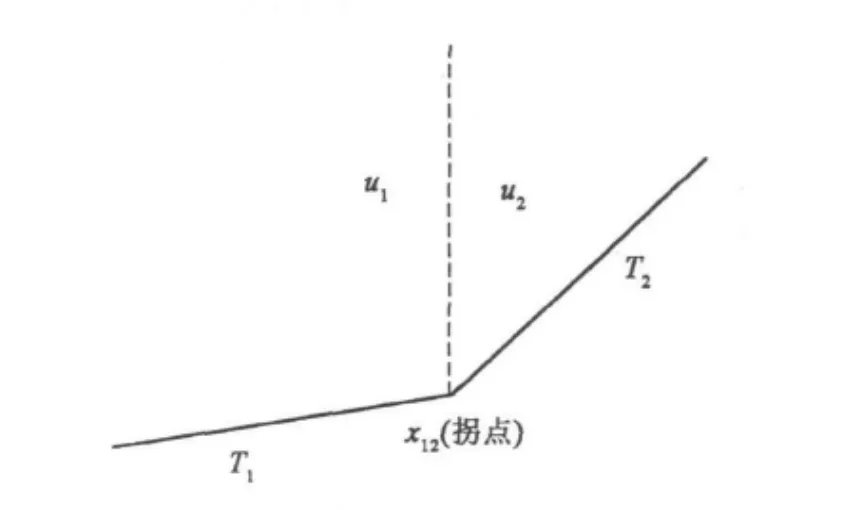
图2 分段线性地形示意图

因此，当地形、障碍物等为分段线性情形时，则电磁场在拐点处的修正系数为[9]

式中：T′1代表端点x12左侧线段的斜率（如图2）；T′2代表端点x12右侧线段的斜率（如图2）。

拐点x12处对应电磁场的变化为

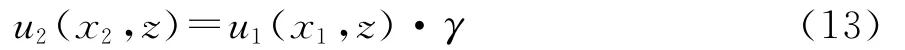
由电波传播理论知，传播因子为电磁波在大气波导空间的场强与自由空间的场强的比值[11]，即

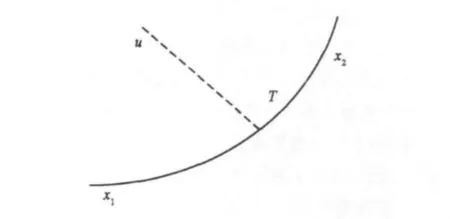
图3 连续性地形示意图

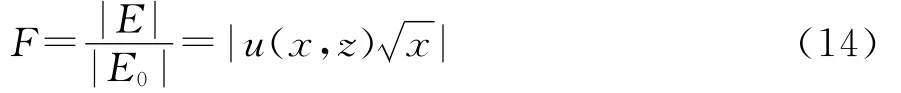
式中E、E0分别为大气波导空间与自由空间接收点场强。

所以在斜率为T1对应拐点x1点的传播因子为

而在斜率为T2对应拐点x2点的传播因子为

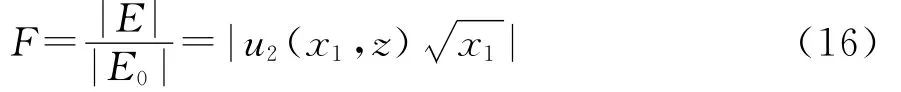
相对于自由空间的归一化功率可表示为[3]

路径传输损耗定义为

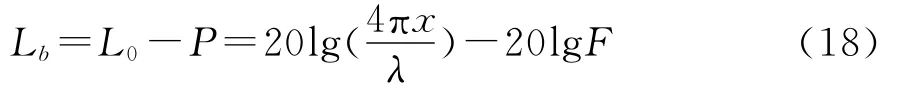
这里，λ为电磁波波长。

3.障碍物模型

根据海面上方障碍物的形状（例如海面上方的岛屿、舰船等），人们在对海面上方的障碍物进行建模时，通常按照障碍物的形状把障碍物分为楔形障碍物及类抛物形障碍物[8]。以下将对这两种不同类型的障碍物进行建模。

3.1 楔形模型

设楔形地形函数为

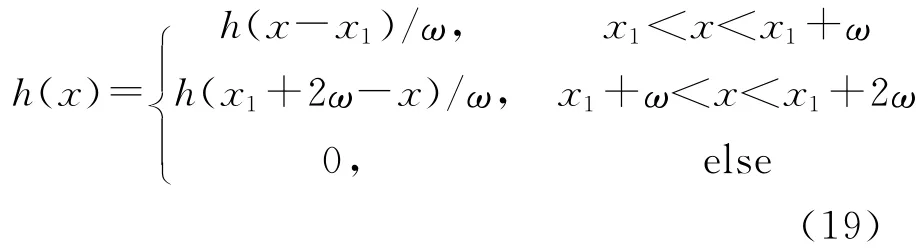
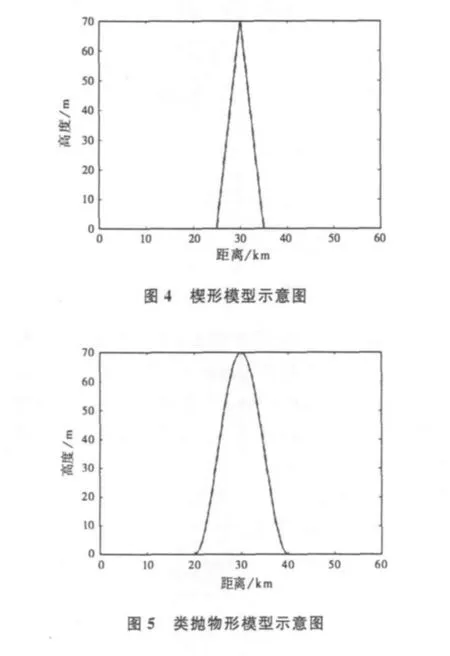
式中：h为峰顶高度；x1为楔形剖面起始点；ω为楔形障碍物的半宽度。图4是以高度为70 m，半宽度为5 km，模型的起点在25 km处的楔形模型为例建立的模型。在实际应用中，可以根据障碍物尺寸的不同而对障碍物进行建模。

3.2 类抛物形模型

当海上障碍物为连绵起伏的岛屿时，由于岛屿的半宽度比较大，而其高度又比较低，此时的岛屿更像一个类抛物形。为了能够准确地对海上障碍物进行建模，人们在楔形模型的基础上对障碍物模型进行了改进，提出了类抛物形模型。

设类抛物形地形函数为

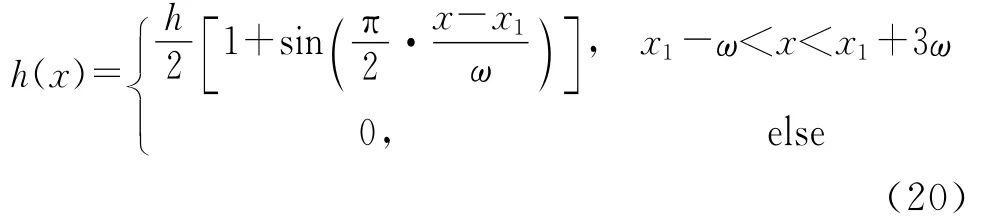
式中：h为峰顶高度；x1－ω为类抛物形剖面起始点；ω为类抛物形障碍物的半宽度。

图5是以高度为70 m，半宽度为10 km，模型的起点在20 km处的类抛物形模型为例建立的模型。同样，在实际应用中，我们可以根据障碍物尺寸的不同而对障碍物进行建模。

4.障碍物对蒸发波导电波传播影响

4.1 单障碍物时蒸发波导内电波传播特性

以下计算取发射天线高度为20 m，频率为10 GHz，极化方式为水平极化的高斯全向天线，蒸发波导高度为30 m，结合前面的分段线性宽角抛物方程求解理论及电磁波传播因子计算式（14）～（16）和传输损耗计算公式（18），分别讨论楔形和抛物形障碍物及障碍物距发射天线不同距离时沿水平距离和某一位置处沿垂直高度分布的电波传播特性。

4.1.1单障碍物蒸发波导内电波归一化功率模型

图6给出了单个楔形障碍物高度为70 m，半宽度为5 km，位置距离发射天线为20 km时在蒸发波导内的电波归一化功率模型，图7则给出了单个抛物形障碍物高度为70 m，半宽度为9 km，位置距离发射天线为22 km时在蒸发波导内的电波归一化功率模型。

从图6和图7可以看出，由于障碍物的存在使得障碍物后方的电磁波强度减弱程度较大，障碍物的存在严重影响着传播过程中电磁波的损耗，当障碍物高于波导高度时，障碍物后方的场强很微弱，电波很难绕过障碍物继续传播，几乎截断了电波传播。

4.1.2 单障碍物时蒸发波导内电波传输损耗随传播距离的变化特性

图8和图9分别给出了单个楔形和抛物形障碍物模型在观测高度为距海面20 m处的蒸发波导层内电波传输损耗随传播距离的分布图，图中并与标准大气和无障碍物情形下电波传播特性作了比较。其中，障碍物高度为70 m，障碍物与发射天线的距离分别为30 km和50 km，楔形障碍物半宽度为2 km，类抛物形障碍物半宽度为5 km.

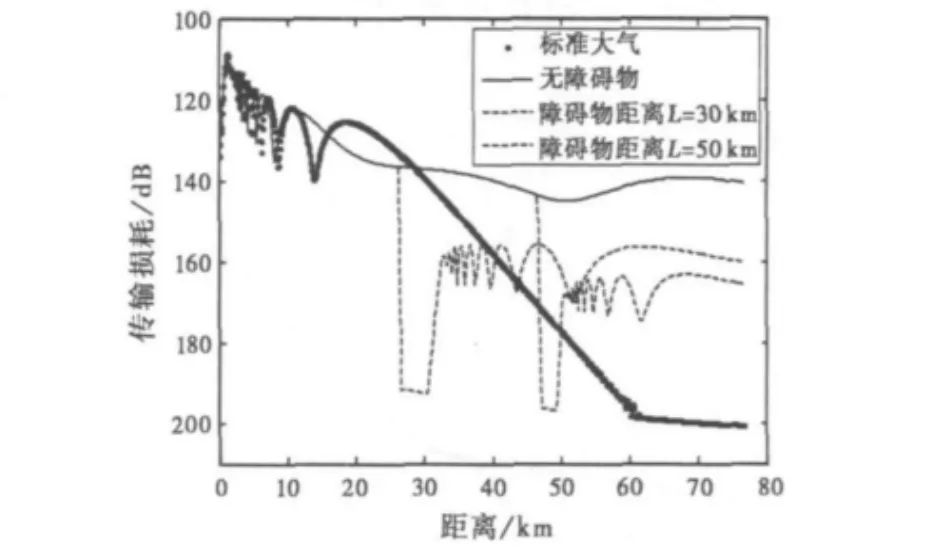
图8 楔形障碍物下电波传播损耗随传播距离的变化

由图8和图9可知，无论是楔形障碍物还是抛物形障碍物，与无障碍物下的波导传输相比，在有障碍物的区域损耗非常大，当绕过障碍物后，可以看到仍会有一些微弱电波能量，这是由于电波经障碍物上方绕射之后部分符合波导传输条件的电波陷获进波导重新形成的二次波导传输效应，可以明显看出能量很弱，随着障碍物与发射天线距离的增大，波导层内的电磁波损耗也随之增加，使得波导层外绕射过障碍物并进入蒸发波导内陷获传播的电磁波的能量及强度都相应的减小，从而使得波导层内电磁波的损耗增加，场强减弱。

图9 抛物形障碍物下电波传播损耗随传播距离的变化

4.1.3 单障碍物时蒸发波导内电波传输损耗随高度变化特性

图10和图11为在距离发射天线70 km处，楔形和抛物形障碍物与发射天线的距离分别为30 km、50 km，障碍物的高度为70 m时电磁波传输损耗随海上垂直高度变化的比较示意图。

通过图10和图11中无障碍物和有障碍物情形下的传播损耗比较可以发现，当在电磁波的传播路径上加入障碍物时，由于障碍物对电磁波的阻碍作用，使得障碍物高度以下部分的电磁波损耗明显增强，同时对障碍物上方附近也产生了较大的影响，可以明显看出上半空间的场基本不受影响；通过30 km处障碍物与50 km处障碍物对电波传播损耗比较发现，距发射天线较远的障碍物对电波的损耗影响比距发射天线较近的障碍物影响要大。

4.2 多障碍物时蒸发波导内的电波传播特性

以下计算利用分段线性宽角抛物方程方法讨论多障碍物下电波在蒸发波导内的传播特性。计算中取发射天线高度为20 m，电波频率为10 GHz，水平极化的高斯全向天线，蒸发波导高度为30 m.

4.2.1 多障碍物蒸发波导内电波归一化功率模型

图12给出了两个抛物形障碍物，第一个高度为20 m，低于波导高度，第二个高度为50 m，高于波导高度，半角宽度均为6 km.从图12可以看出，当障碍物高度低于波导高度时，电波可以绕过障碍物继续在波导内传输，当第二次遇到了高于波导高度的障碍物时，电波几乎被截断，很难绕过障碍物继续传播。可见，障碍物的高度对电磁波在蒸发波导内的传播有很大的影响。

4.2.2 多障碍物时蒸发波导内电波传输损耗随传播距离的变化特性

图13给出了前后两个抛物形障碍物高度分别为20 m和50 m情况下，观测高度为距海面20 m时电波在波导中的传播损耗随传播距离的变化比较图。通过图13可以看出，与无障碍物时结果相比，随着传输距离的增大，多个障碍物的存在使得电波传输损耗明显增大，并且可以看出前后两个障碍物高度的不同对电波传输损耗影响不同，障碍物高度越高，电波传输损耗越大。

图13 不同传播距离抛物形障碍物下电波传播损耗

4.2.3 多障碍物时蒸发波导内电波传输损耗随高度的变化特性

图14给出了单个障碍物高度为40 m位于30 km处和多障碍物高度分别为20 m和50 m位于20 km和40 km处，在距离70 km处电波在蒸发波导内传播损耗随高度变化的分布比较，通过图14可以看出，障碍物的存在都更大地增大了电波传输损耗，且多障碍物存在时比单个障碍物存在时，不同障碍物情形都严重地影响着电波在蒸发波导内的传播特性。

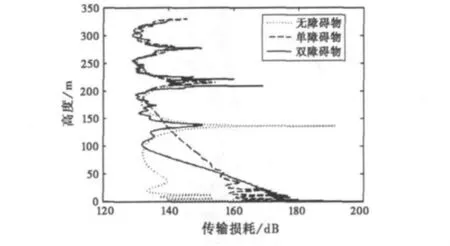
图14 不同抛物形障碍物下电波传播损耗随高度的变化

5.结 论

本文研究了含障碍物情形下蒸发波导电波传输特性，推导了分段线性宽角抛物型方程的分步傅里叶解，通过数值计算表明，障碍物的存在增大了电波在蒸发波导内的传输损耗，障碍物的高度越高对电波在波导内的传输影响越大，当障碍物高度低于波导高度时，电波可以绕过障碍物继续沿波导传播，当障碍物高度高于波导高度时电波很难绕过障碍物在波导内继续传播。多障碍物存在时对电波在蒸发波导内的传播特性影响大于单个障碍物存在时的影响。需要说明的是本文尚未分析考虑障碍物表面介电特性对蒸发波导电波传输特性的影响，分析案例也仅限于光滑海面下的简单障碍物模型研究，有关粗糙海面下复杂障碍物对蒸发波导环境中电波传播的影响及有关传输损耗实验测量验证工作还需作深入研究。

[1] 戴福山.海洋大气近地层折射指数模式及其在蒸发波导分析上的应用[J] .电波科学学报，1998，13（3）：280－286.DAI Fushan.The refractivity models in the marine atmospheric surface layer and their applications in the evaporation duct analysis[J] .Chinese Journal of Radio Science，1998，13（3）：280－286.（in Chinese）

[2] 刘成国，潘中伟.中国低空大气波导的极限频率和穿透角[J] .通信学报，1998，19（10）：90－95.LIU Chengguo，PAN Zhongwei.The cut off frequencies and critical angles of troposphere ducts in China[J] .Journal on Communications，1998，19（10）：90－95.（in Chinese）

[3] 姚展予.大气波导特征分析及其对电磁波传播的影响[J] .气象学报，2000，58（5）：606－616.YAO Zhanyu.The analysis on characteristics of atmospheric duct and its effects on the propagation of electromagnetic wave[J] .Actam Meteorologica Sinica，2000，58（5）：606－616.（in Chinese）

[4] 郭立新，李宏强，杨 超，等.改进的DMFT算法研究粗糙海上蒸发波导中的电波传播特性[J] .电波科学学报，2009，24（3）：414－421.GUO Lixin，LI Hongqiang，Yang Chao，et al.Characteristic of radio wave propagation in the evaporation duct environment over the rough surface by the improved DMFT algorithm[J] .Chinese Journal of Radio Science，2009，24（3）：414－421.（in Chinese）

[5] LEVY M F.Parabolic Equation Methods for Electromagnetic Wave Propagation[M] .London：IEE Press，2000.

[6] BEILIS A，TAPPERT F D.Coupled mode analysis of multiple rough surface scatter[J] .Acoust.Soc.A－mer.，1979，66（3）：811－826.

[7] BARRIOS A E.A terrain parabolic equation model for propagation in the troposphere[J] .IEEE Trans.Antennas and Propagation，1994，42（1）：90－98.

[8] THOMSON D J，CHAPMAN N R.A wide－angle split－step algorithm for the parabolic equation[J] .Acoust.Soc.Amer.，1983，74（6）：1848－1854.

[9] DONOHUE D J，KUTTER J R.Propagation modeling over terrain using the parabolic wave equation[J] .IEEE Trans.Antennas and Propagation，2000，48（2）：260－277.

[10] DOCKERY G D，KUTTER J R.An improved impedance boundary algorithm for Fourier split－step solution of the parabolic equation[J] .IEEE Trans.Antennas and Propagation，1996，44（12）：1592－1599.

[11] 胡绘斌.预测复杂环境下电波传播特性的算法研究[D] .长沙：国防科技大学，2006.HU Huibin.Study on the Algorithms of Predicting the Radio Propagation Characteristics in Complex Environments[D] .National university of defense technology，2006.（in Chinese）