金融危机对股市间波动的联动性影响

饶 卫，闵宗陶

(西安交通大学 经济与金融学院，陕西 西安 710061)

一、引 言

2007年美国引发的金融危机，使全球经济体受到相当严重的冲击，全球股市均出现暴跌现象，引起连锁效应或可归因于金融市场自由化与全球科技迅速发展的影响，股市间的信息得以迅速地传递，因而各股市间关联性与互动关系日趋整合。若能了解金融危机对股市间波动的联动性，便可为投资人在面对重大事件时进行跨国投资提供参考依据，以分散投资风险。

过去相关文献认为资产报酬率假设服从连续的扩散随机过程，不适合解释资产报酬上可能存在大量不可预测事件的冲击影响，对于事件的冲击影响所产生的变异程度不可忽略，Ball和Torous，Jarrow和 Rosenfeld与Akgiray和 Booth指出GARCH系列模型可以捕捉到报酬率波动性的自相关现象，但无法解释股价报酬率出现的不连续情 形［1］－［3］，Jorion ， 徐 有 俊 等 与 Das 和Sundaram一致认为未考虑间断跳跃的特性时，将可能造成误设股价行为的问题，因此，考虑股价加入间断跳跃的特性是必要的［4］－［6］。Merton尝试使用跳跃—扩散过程 (Jump－Diffusion Process)对报酬率的厚尾与偏态现象进行解释［7］，蔡义杰等发现报酬序列存在着间断的跳跃行为的统计特性［8］，Jorion提出ARCH模型结合跳跃—扩散模型，其实证发现此模型有较佳的解释能力［4］，Chan和Maheu加入跳跃强度随着时间改变ARJI(Autoregression Conditional Jump Intensity)，其实证发现较GARCH模型结合跳跃—扩散模型更能解释股价报酬率出现不连续情形［9］。

综合上述文献可知，考虑股价间断跳跃的特性是必要的。因此，本文采用2004年6月30日至2010年6月30日数据，利用ARJI证实新加坡、日本、中国香港、美国与中国大陆股市是否存在不连续性的跳跃，并将股价指数报酬的波动性区分为跳跃过程所引发的变异数与扩散所引发的变异数，更进一步计算跳跃过程所引发之变异占整体变异的比重，以了解跳跃风险的重要性。

最后，本文利用ARJI模型所得到波动性后，再进行美国、日本、中国香港、新加坡与中国大陆股市波动性的连动关系分析，由于受到金融危机影响后，投资人要选择哪些国家投资更是令人关切的问题之一，本文利用Peasran和Shin建立的向量自回归模型脉冲响应函数 (Generalized Impulse Response Function)来探讨金融危机后各国股市间波动性冲击的影响，以寻找出受其它国家或地区冲击影响较小的国家或地区［10］，所得结果能为投资者在美国、日本、中国香港、新加坡与中国大陆股市投资提供决策参考依据，这是一个值得探讨的课题。

二、实证模型

1.ARJI模型

传统假设资产报酬率服从连续的扩散随机过程，可表示为:

其中，Pt为资产价格，dPt/Pt为资产报酬率，dZt为标准化的维纳过程 (Wiener Process)，并假设资产报酬率服从平均数为μ标准差为σ的常态分布。Bates认为市场跳跃强度可能会随着时间而改变，将跳跃强度设定为具有随时间变动的特性［11］，因此，本文采用Chan和Maheu将跳跃强度设定为ARMA过程［9］，并且考虑资产报酬率的GARCH效果，将此模型称为ARJI。资产报酬率的公式表示如下:

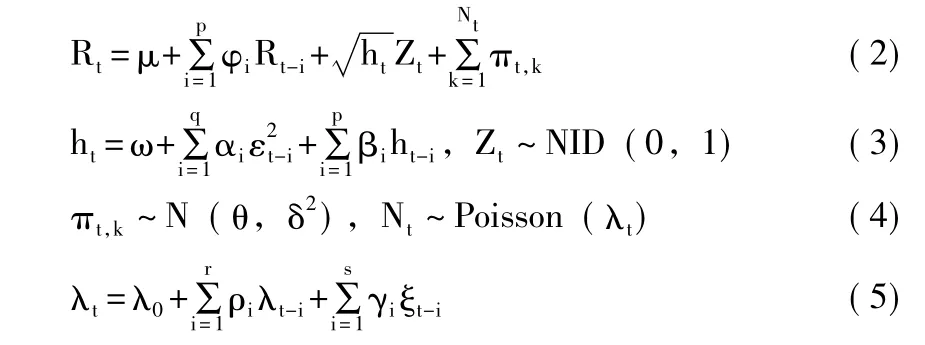
其中，ht为Rt的条件异质变异数方程式，其服从GARCH(p，q)过程。εt为平均数方程式的误差项。Zt～NID(0，1)为标准化的维纳过程。假设跳跃大小 (πt，k)与标准化的维纳过程 (Zt)为独立。跳跃大小服从平均数为θt与变异数为的常态分布。Nt～Poisson(λt)为跳跃强度分布，在此处定义 λt≡E［NtΩt－1］，表示随时间变动的跳跃强度为条件期望值且服从内生的ARMA(r，s)过程，将表示为为第 t －1期的跳跃大小，ξt－1为第t－1期跳跃的误差项。，v 为((Nt+1)×1)向量，其第j个元素为j－1，而是利用贝氏定理 (Bayes Rule)计算t期的事后条件概率向量，其中1为((Nt+1)×1)元素都为1的常数向量，Θ为矩阵相对应元素相乘的运算子。为 λ t的波氏概 率 密 度 函 数 向 量

其第j+1个元素为P(Nt=j Ωt－1)=，其意义为在Ωt－1条件下跳跃次数为j的概率，而Ωt－1={R1，...，Rt－1} 定义为 t －1 期所有的信息集合，Πt为在t期的常态概率密度函数向量，其第j+1个元素可表示为:

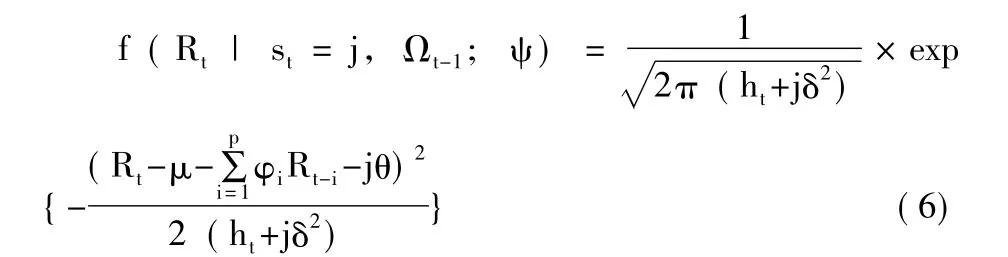
其中，ψ = ( μ，φi，ω，αi，βi，θ，δ2，λ0，ρi，γi)为待估参数向量。在上述的设定下，对数概似函数可表示为:

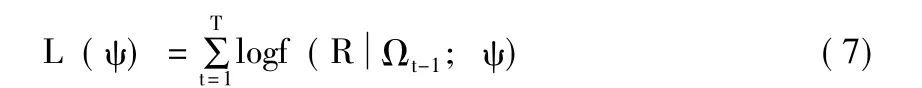
2.VAR模型

VAR模型所推导的脉冲响应函数分析的自回归模型设定为:

其中，Yt为总变异数n×1向量，βi为 n ×n系数矩阵，Yt－i是由Yt向量第i期滞后期数所组成的n×n向量，而εt为残差项。模型的最佳滞后期数的长短，以AIC与SBC准则来决定最合适的滞后期数。

三、实证分析过程与结果

1.数据来源与处理

本文以中国大陆、中国香港、日本、美国与新加坡股市为研究对象，选取股价指数分别为中国上证综指 (SCI)、香港恒生指数 (HKHSI)、日经225指数 (Nikkei225)、标准普尔500指数(S＆P500)与新加坡海峡时报指数 (SSI)来探讨金融危机对于彼此间股票市场的互动关系。总样本期间为2004年6月30日至2010年6月30日，数据来源为Blommberg数据库的每日收盘数据。利用每日股价指数来计算股价指数报酬率，股价指数报酬率定义为:

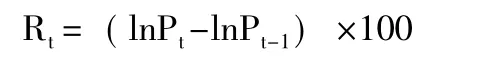
其中，Rt为第t期股价指数日报酬率，Pt为第t期的股价指数的收盘价，Pt－1为第t－1期股价指数的收盘价。

先将各国股价指数报酬率进行ARJI模型估计后，再将各国股价指数报酬率的条件变异数抽出，然后探讨金融危机期间与非金融危机期间各股市间的联动性，由于样本数据显示各国交易日与休市日存在不尽相同，为求数据的稳定性与一致性，因而本文将除去交易日期无法对应的数据，将此数据区分为2004/6/30至2007/7/30与2008/9/1至2010/6/30为非金融危机期间及2007/8/1至2008/8/31为金融危机期间。

2.基本描述性统计

表1为各股市的股价指数报酬率的基本描述性统计量分析结果。在5%的显著水平下，SCI、S＆P500、Nikkei225、SSI与 HKHSI股价指数报酬率序列的平均数都不显著异于0，偏态有Nikkei225、SSI与 HKHSI显著大于 0，即 SCI、Nikkei225与HKHSI的股价指数报酬率都呈现左偏，而SCI、S＆P500呈现显著小于0，即表示股价指数报酬率都呈现右偏。峰态都呈现显著大于3，即各股价指数报酬率都属于高狭峰，Jarque－Bera检验统计量都呈现显著，即表示都否定其为常态分布，可部分归因于序列自相关。在10%的显著水平下，各股价指数报酬率序列滞后12期的Ljung－Box Q检验统计量都呈现显著，即表示各股价指数报酬率序列都存在着自相关。在5%的显著水平下，各股价指数报酬率序列平方滞后12期的Ljung－Box Q检验统计量都呈现显著，即表示各股价指数报酬率序列平方都存在着自相关，可部分归因于条件异质变量，即表示较大的报酬率趋势伴随着同方向较大报酬率变动。

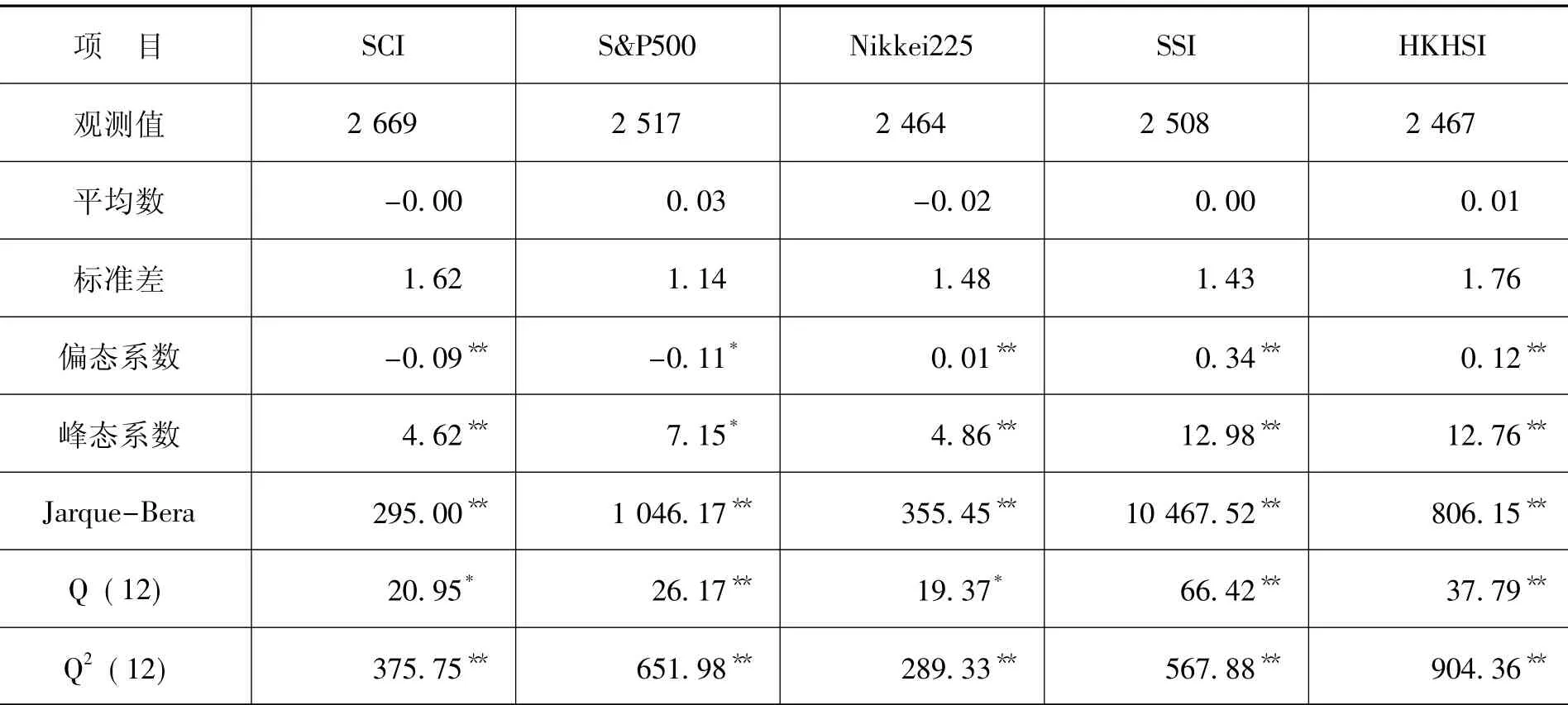
表1 基本描述性统计

3.单位根检验

若研究未考虑时间序列数据是否为非平稳过程，将可能造成不正确的研究结果，因此，对于时间序列数据必须先进行单位根检验，本文利用Augmented Dickey Fuller(ADF)、Phillip－Perron(P－P)与 Kwiatkowski－Phillips－Schmidt－Shin(KPSS)检验进行单位根检验，若存在单位根时，则对此时间序列数据进行差分，直到此序列成为平稳过程。其中，ADF与P－P单位根检验零假设都为存在单位根，KPSS单位根检验法为不存在单位根零假设，对各股市报酬率序列的平稳检验进行测试分析。由表2得知，ADF与P－P单位根检验法显示，在5%显著水平下，各股市报酬率序列都拒绝零假设为非平稳的单位根检验，KPSS单位根检验法显示，在5%显著水平下，股市报酬率序列都无法拒绝零假设为平稳的单位根检验。综合上述结果可得知，SCI、Nikkei225、S＆P500、SSI与 HKHSI股价指数的报酬率数据都为平稳的时间数列数据。

表2 各股市报酬率序列的单位根检验表

4.ARJI模型的应用

本文利用ARJI模型来计量各股价指数报酬率的变化，表3为各国股价指数报酬率的ARJI模型估计与检验结果。由标准化冲击平方的Linug－Box Q检验统计量未呈现显著，即表示模型的残差标准化冲击平方序列无序列相关，在异质性检验发现都未呈现显著存在异质性。由ARJI模型的估计结果显示，在10%显著水平下，SSI的跳跃大小的平均数θ呈现显著，其余各国股价指数报酬率的跳跃大小的平均数θ与变异数δ2在5%显著水平下都显著，即表示各国股价指数报酬率均存在着异常信息所造成瞬时的跳跃行为，其中，报酬率受到异常信息所造成瞬时的跳跃平均数介于－1.55至－0.21之间，即表示异常信息所引起的跳跃对于报酬为负面影响，其异常信息所造成瞬时的跳跃行为波动程度介于0.10—3.38之间。在10%显著水平下，SSI的股价指数报酬率的跳跃频率λ0呈现显著，其余各国股价指数报酬率的跳跃频率λ0、ρ与γ在5%显著水平下都显著，即表示在异常信息所产生的跳跃频率是随着时间而变动的。综合上述，各国股价指数报酬率的跳跃大小与跳跃频率结果，不连续跳跃过程是影响报酬率不可忽视的重要因素，支持Kim和 Mei与Chang和 Kim指出不可预期事件的因素将存在不连续性的跳跃的结论［12－13］。

本文针对不同国家间的跳跃强度作综合比较，以Pearson的相关系数统计方法发现不同国家间的跳跃强度有显著相关。由跳跃强度发现各国间断跳跃行为存在着市场效率上的差异及其背后可能原因。

由于Kim和Mei与Chang和Kim认为市场上存在不连续性跳跃影响［12－13］，因而本文利用Nimalendran［14］提出估计算总变异数为 Vt=ht+λt(θ2+δ2)，即将各国股价指数报酬率的总变异数区分为跳跃过程所引发的变异数与扩散过程所引发的变异数，再计算跳跃过程所产生的变异数占整个跳跃—扩散过程的比例，故由此比例进而了解波动对于异常信息反应的程度大小。由表3的B部分可得知，各国股价指数报酬率的跳跃过程所引发的变异占整体变异的比重介于16%—34%之间，又以S＆P500股价指数报酬率的跳跃过程所引发的变异占整体变异的比重34%为最高，通过跳跃过程所引发的变异占整体变异的比重可了解跳跃风险的重要性，因此，跳跃过程所引发的变异是不可忽视的重要因素。

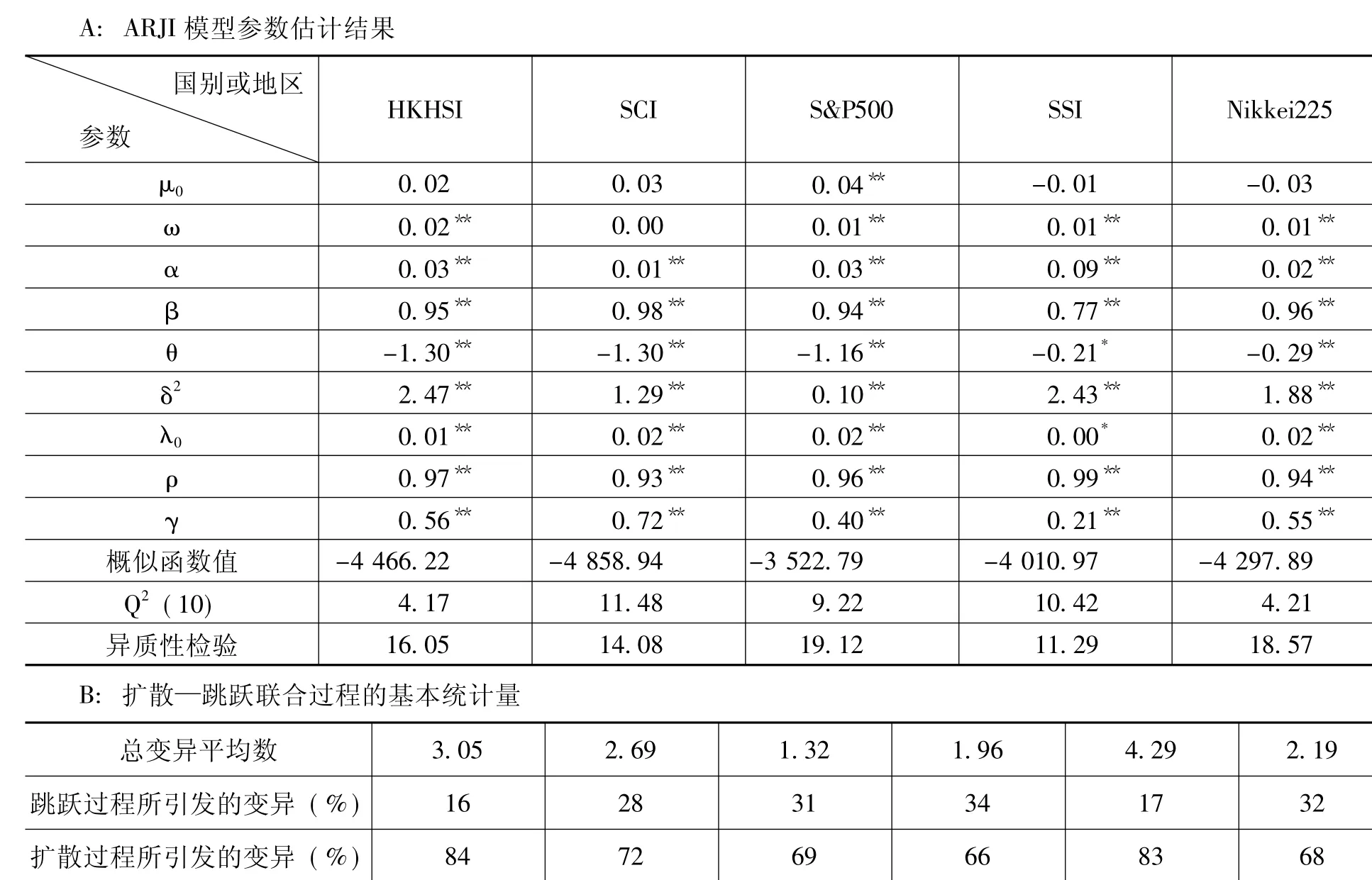
表3 ARJI模型估计与检验

5.各国股市间波动性的影响

以往的文献探讨金融危机事件对异常报酬的波动性的影响，对于金融危机事件所产生不连续性跳跃波动的研究相当的缺乏，对于金融危机期间与非金融危机期间的总变异数、扩散变异数与跳跃变异数是否存在着差异，本文比较金融危机期间与非金融危机期间的总变异数、扩散变异数与跳跃变异数的平均数检验。进行平均数检验前须检验两样本的变异数是否相同，才可决定合适的检验统计量，本文利用Levene's检验，只有SCI的总条件变异数的变异数为相同，因而利用t检验统计量，其余都为变异数不相同，则参考Forbes和 Rigobon［15］修正过的 t检验统计量。

表4为总条件变异数的平均数检验结果。在总条件变异数的平均数检验发现，大部分国家在金融危机期间的平均总变异数是大于非金融危机期间的，只有SCI没有显著的差异，即金融危机对于SCI的影响程度相对而言较小。但S＆P500在金融危机期间的平均总变异数是大于非金融危机时期，即表示金融危机对S＆P500的影响程度较大。在扩散变异数的平均数检验发现，大部分国家在金融危机期间的平均扩散变异数是大于非金融危机时期的。在跳跃变异数的平均数检验发现，大部分国家在金融危机期间的平均跳跃变异数是大于非金融危机期间的。

表4 总条件变异数、扩散变异数与跳跃变异数的平均数检验

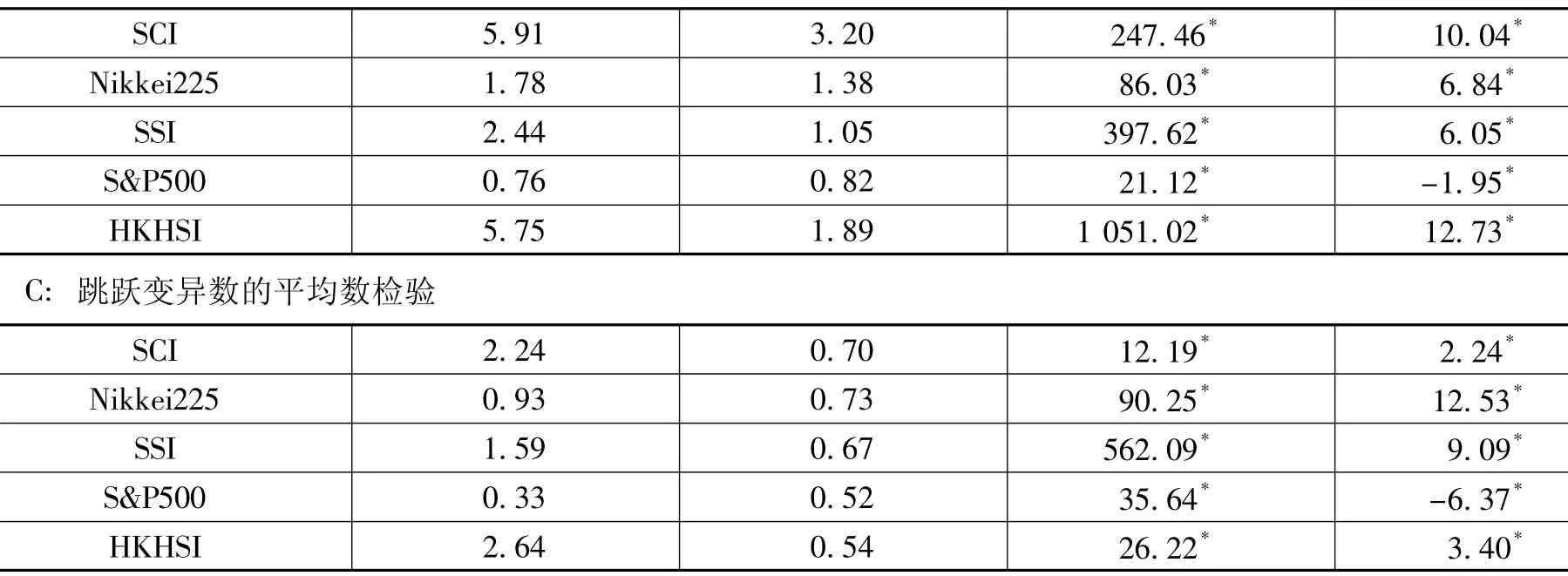
注:① 由于受论文篇幅限制，这里省略了金融危机期间的波动性冲击反应图，有兴趣的读者请与作者联系。*表示5%的显著水平下呈现显著。②Levene's Test为检验变异数是否相同，零假设为金融危机与非金融危机变异数相同。③t值统计量为检验平均数是否有差异，零假设为金融危机与非金融危机平均数相同。④变异数不相同时的t统计量参考Forbes和 Rigobon［15］。

综上所述，以上国家或地区都受到金融危机事件的影响，使得金融危机事件对 SCI、Nikkei225、SSI与HKHSI的波动性在金融危机期间呈现显著的差异。因此，投资人在进行跨国投资组合的决策时，SCI与SSI市场是值得考虑的投资市场。

本文利用Pearson相关检验在金融危机前后各国家间的波动性的关系。由表5可知，不管是否为金融危机前后，在波动性的Pearson相关系数检验都呈现显著相关，而在金融危机后的波动性相关系数都比在金融危机前的相关程度更高，即显示股市崩盘后各国或地区股市间相依程度增强，除了SCI与 Nikkei225、SSI与 HKHSI在金融危机前的波动性相关系数比在金融危机后的波动性相关系数高。在金融危机前各国或地区间的波动性呈现有正相关与负相关，但在金融危机后各国间的波动性都呈现正相关。

表5 波动性的Pearson相关检验

本文利用脉冲响应函数来探讨金融危机后各国股市间波动性冲击的影响。①在进行脉冲响应函数分析之前，若未考虑时间序列数据是否为非平稳过程，将可能造成不正确的研究结果，因此对于时间序列数据必须先进行单位根检验，本文利用ADF、P－P与KPSS检验进行单位根检验，其结果都为平稳序列。由单位根检验得知各国总条件变异数都为平稳，再进行VAR模型分析，根据AIC与SBC准则决定其模型最佳滞后阶数为6期。

在金融危机期间 SCI、Nikkei225、SSI与HKHSI都受到其它国家或地区干扰项影响程度较为持续，而SCI与SSI受到其它国家或地区干扰项影响是暂时性的，其中，S＆P500的标准差干扰项对于SCI与SSI几乎无影响。综合上述发现SSI股市波动性具有独立性的特性，其干扰项的影响对其他国家最为显著，其次为SCI股市波动性。此外，本文利用S＆P500股市投资组合对各国影响的大小进行排序，发现各国或地区受S＆P500一单位标准差干扰项的持续性影响依照大到小的相对顺序分别为HKHSI、SSCI、SCI、Nikkei225。因此，考虑SSI或SCI市场纳入投资组合将提供投资人在进行跨国投资组合的决策的参考。

四、结 论

本文以ARJI模型探讨金融危机对美国、日本、中国香港、美国与中国大陆股市产生跳跃频率与跳跃所引起的变异，并比较总变异、跳跃所引起的变异与扩散所引起的变异，最后利用脉冲响应函数来分析新加坡、日本、中国香港、美国与中国大陆股市波动性间的关系。

实证结果发现由ARJI模型的估计结果显示，各国或地区股价指数报酬率均存在着异常信息所造成瞬时的跳跃行为与跳跃频率是随着时间变动，各国股价指数报酬率的跳跃过程所引发的变异占整体变异的比重介于16%—34%之间，跳跃过程所引发的变异是不可忽视的重要因素。本文利用波动性的Pearson相关检验发现各国或地区波动性相关关系都呈现显著，在金融危机后的波动性相关系数几乎都比在金融危机前的相关程度更高，除了与日本、新加坡与中国香港的波动性相关系数较低。在金融危机前各国间的波动性呈现正相关或负相关，但在金融危机后各国间的波动性都呈现正相关。此外，利用脉冲响应函数分析探讨金融危机后各国股市间波动性冲击的影响，研究结果发现新加坡股市波动性具有独立性的特性，其次为中国大陆股市波动性，因此，可以为投资人在进行跨国投资组合时提供决策参考。综合上述两个结论，投资人在进行跨国投资组合决策时，新加坡或中国大陆股市是值得考虑的投资市场。

［1］Ball，C.A.，Torous，W.N.On Jumps in Stock Returns［J］.Journal of Financial Quantitative Analysis，1985，(10):337－351.

［2］Jarrow，R.A.，Rosenfeld，E.R.Jump Risks and the Intertemporal Capital Asset Pricing Model［J］.Journal of Business，1984，57(3):337－351.

［3］Akgiray，V.，Booth，G.G.Compound Distribution Models of Stock Returns:An Empirical Comparison［J］.Journal of Financial Research，1986，(10):259－280.

［4］Jorion，P.On Jump Processes in the Foreign Exchange and Stock Markets ［J］.The Review of Financial Studies，1988，(1):427－445.

［5］徐有俊，王小霞，贾金金.中国股市与国际股市联动性分析——基于DCC－GARCH模型研究［J］.经济经纬，2010，(5).

［6］Das，S.R.，Sundaram，R.K.Of Smiles and Smirks:A Term Structure Perspective ［J］.Journal of Financial and Quantitative Analysis，1999，34(10):211－240.

［7］Merton，R.C.The Impacton Option Pricing of Specification Error in the Underlying Stock Price Returns［J］.The Journal of Finance，1976，31(2):333－350.

［8］蔡义杰，周雨田，李丹.次贷危机下美国和全球股市之联动［J］. 国际金融研究，2009，(9).

［9］Chan， W.H.， Maheu， J.M.Conditional Jump Dynamics in Stock Market Return ［J］.Journal of Business and Economic Statistics，2002，20(3):377－389.

［10］Pesaran，M.H.，Shin，Y.Impulse Response Analysis in Linear Multivariate Models ［J］.Economics Letters，1998，58(1):17－29.

［11］Bates，D.S. Jumps and Stochastic Volatility:Evidence from the Options Markets［J］.Journal of Finance，1996，46(7):1009－2049.

［12］Kim，H.Y.，Mei，J.P.What Makes the Stock Market Jump?An Analysis of Political Risk on Hong Kong Stock Returns［J］.Journal of International Money and Finance，2001，20(7):1003－1016.

［13］Chang，K.H.，Kim，M.J.Jump and Time－Varying Correlations in Daily Foreign Exchange Rates ［J］.Journal of International Money and Finance，2001，20(5):611－637.

［14］Nimalendran，M.Estimating the Effects of Information Surprises and Trading on Stock Returns Using a Mixed Jump － Diffusion Model ［J］.Review of Financial Studies，1994，(7):451 － 473.

［15］Forbes， K.， Rigobon， R.No Contagion， only Interdependence:Measuring Stock Market Comovements［J］.Journal of Finance，2002，57(5):2223－2261.

［16］陈丽娟.基于EGARCH－M模型和沪深300指数的股市风险分析［J］.东北财经大学学报，2010，(2).