基于模态理论的封头分层缺陷扩展安全分析

姚 舜

（广西区特种设备监督检验院，广西南宁530219）

一立式压力储罐2006年11月制造，2007年8月在某水电站投入运行，基本参数见表1。本储罐出厂时有质量证明书、产品合格证、监督检验证书，铭牌完整，但缺少竣工图。封头无单独的质量证明书。对接焊缝经20%射线检测，按JB-4730-2005Ⅱ级合格，整体热处理后，水压试验（PT=8.5MPa）合格。

表1 压力储罐基本参数

投入使用二年半后，2010年1月第一次对压力储罐进行全面检验，进行测厚检测时，发现封头存在大面积分层缺陷，上封头的整个椭圆面及直边段的部分位置，都存在分层缺陷。缺陷深度距表面约为12.6～15.6 mm，且为连续分层缺陷，分层缺陷与表面基本平行。2010年检验结论是储罐监控使用，封头直边段的分层缺陷作为重点监控部位，2011年1月又对本储罐进行了检测，发现直边段缺陷有扩展。

现已有文献分析了分层缺陷的安全及可靠性[1]，但其分层缺陷面积比较少，对本文所分析的大面积分层缺陷有一定的参考价值，但从文献中鲜见从整体分析压力容器的动力学特性，GB150也几乎全部按静力分析来设计压力容器[2]。实际上当压力容器受到交变载荷或突然冲击(如地震)时，容器的整体动力特性对设备的安全运行更显得重要，故本文拟用基于模态理论的方法，对缺陷扩展进行安全分析。

1 模态分析基本理论

模态分析是研究结构动力特性一种方法，是系统辨别方法在工程振动领域中的应用。模态是机械结构的固有振动特性，每一个模态具有特定的固有频率、阻尼比和模态振型。振动模态是弹性结构的固有的、整体的特性。如果通过模态分析方法，搞清楚了结构物在某一易受影响的频率范围内各阶主要模态的特性，就可能预言结构在此频段内，在外部或内部各种振源作用下的实际振动响应。因此，模态分析是结构动态设计及设备的故障诊断的重要方法[3]。

1.1 模态分析基本原理

动力学分析的基本方程为

其中，

M是结构的质量；

ü是结构的加速度；

I是结构中的内力；

P是所施加的力。

对于无阻尼系统

I=Ku，

K为结构的刚度矩阵。

实际上结构具有多个固有频率，固有频率可以通过分析结构要无载荷（也就是在式（1）中P=0）时的动态响应而得到，此时运动方程为

上述方程解的形式为

将式（3）带入式（2），得到特征值问题方程

其中，λ= ω2。

该系统具有n个特征值，记λj为第j个特征值，它的平方根ωj是结构的第j阶固有频率，并且Φj是相应的第j阶特征向量，特征向量也即所谓的模态（也称振型），它是结构在第j阶振型下的变形状态。

在线性情况下，结构在载荷作用下的动力响应，可以用固有频率和振型来表示，即结构的变形，可以采用振型叠加技术由各振型的组合得到，每一阶模态都要乘以一个标量因子αi，模型中位移矢量u定义为

这一技术只是在小变形、线弹性材料、无接触等条件下有效，实际上在现实生活中，更多的是非线性的，系统在载荷作用下的频率响应，可以是数个频率的合成，或者是某个频率的倍频，但结构的响应往往取决于相对较少的前几阶振型。

2 基于有限元的储罐整体模态分析

模态分析一般使用的方法有2种，即实验和有限元计算法。随着计算机技术的快速发展，有限元计算模态法，得到越来越得广泛应用。本文选用这种方法，选择了目前较为流行的有限元分析软件ABAQUS进行储罐整体的模态分析[4～5]。

按照设备具体尺寸，进行实体建模，建成后的实体模型如图1所示

图1 储罐实体模型

分析时取材料属性参数如下：

弹性模量 E=2.06×1011Pa，

泊松比μ=0.3，

密度 ρ=7.8×103kg/m3。

对模型选择线性四面体单元（C3D4）进行网格单元划分，共得15809个四面体单元。选择分析前15阶频率及其振型，最后进行有限元求解，得到的前15阶频率及其值如图2所列。

图2 设备固有频率及其振型值框图

选择1阶、2阶、3阶及15阶振型如图3所示。

图3 各阶振型图

选择封头顶部一个节点18，绘制节点随模态变化的位移曲线，如图4所示。

图4 节点18随着模态变化的位移曲线

结果分析：

从模型的振型和节点位移图可以看出，当其振动频率达到其固有频率时，其振动幅度远远超过其允许的位移量，其中部分振型封头顶部的位移量达到1m，这将可能直接导致结构的破坏。

3 分层缺陷扩展成因分析

本文的研究对象，是椭圆封头顶部大面积分层缺陷，其所受载荷如图5所示，交变周期是15～30 min，压力波动范围在5.4～6.3 MPa之间，压力幅0.45 MPa，按常规说这载荷波动幅值不太剧烈，但进行声发射检测时，发现有声发射检测信号，而且还是强活性，同时经过连续2年的定期检测，发现分层缺陷有扩展。

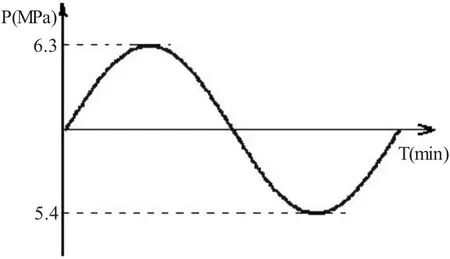
图5 工作载荷运行图

结合对本文第2节的模型固有频率分析可知，其 1阶和2阶频率分别为110.17 Hz，110.33 Hz，实际工作载荷的波动频率为0.000555～0.00111 Hz之间，通过对比发现，实际工作载荷的运行频率和设备固有频率存在倍频关系。

现在生活中，虽然工作频率和设备固有频率相离较远，但由于工况复杂，多数存在强非线性关系，如存在倍频关系，更易导致设备的破坏。故很有能是由于工作载荷的频率和设备的固有频率存在倍频关系，导致本文所研究设备分层缺陷的扩展。

4 结束语

通过对具有分层的设备进行整体模态分析，试图从动力学角度，对设备的安全进行分析。通过分析设备前15阶固有频率及其振型，结合设备所受工作载荷的工作频率分析可知，工作载荷的频率和设备的自身固有频率，存在倍频关系，设备分层缺陷的扩展，很有可能是由于工作载荷频率和固有频率存在这种强非线性关系引起的倍频所导致。通过本文的研究，可以给设备设计单位提供另一种保证安全的参考设计措施。

[1]盛水平.80 m3液化气卧罐封头夹层缺陷的安全分析[J].压力容器，1993，10(5):76-79.

[2]GB 150-1998，钢制压力容器[S].

[3]闻邦椿.机械振动理论及应用[M].北京：高等教育出版社，2009.

[4]庄 茁，由小川，廖剑晖，等.基于ABAQUS的有限元分析与应用[M].北京：清华大学出版社，2009.

[5]刘 展.ABAQUS 6.6基础教程与实例详解[M].北京：中国水利水电出版社，2008.