基于激励效用的理想解法

2011-06-02王金山

重庆理工大学学报(自然科学) 2011年12期

王金山，文秘

(陆军军官学院，合肥 230031)

理想解法［1］是一种基于理想点的决策方法，其基本思路是定义决策问题的最优向量和最劣向量，计算各评价单元与最优向量和最劣向量的距离及相对贴近度，并以相对贴近度的大小进行决策。但理想解法存在“理想点”不理想，标准化不成比例，刻意避开主观偏好的缺点。针对这些缺点，本文提出了基于激励效用的理想解法，利用激励效用化方法对决策矩阵进行处理，科学合理地描述了决策者的主观偏好，提高了可信度，能更好地解决多指标决策问题。

1 激励效用

1.1 激励

按照美国心理学家费斯延格的公平理论［2］，对组织中员工的有效激励源于员工个体对组织公平性的认识水平，即员工个体通过“横向”、“纵向”2种形式的比较，来判断其所得报酬的公平程度。同样，决策者在2种方案中间作出选择时通常面临如下的激励判断:

1)QAIA=QBIB，表示2种方案是一致的，没有激励产生的偏好。

2)QAIA＞QBIB，A方案的相对收益要比付出多，产生了正向的激励，决策者偏好于A方案。

QA为自己对A方案所获报酬的感觉;IA为自己对A方案投入量的感觉。

“人们对激励做出反应，其余内容都是对此的解释”［3］，决策者的偏好是由于某种激励产生的。激励值的大小是一个很好的描述效用值的指标。

1.2 激励指标的建立

激励的大小除与收益、付出的相对大小有关外，还与他们的差值有关，因此令:

其中:p为激励指标，刻画激励的大小;Q为对方案所获报酬的感觉;I为对方案合理投入量的感觉。当p＜0为负向激励，p＞0为正向激励，p=0没有激励，p越大激励程度越高。如果在方案确定之前不知道合理的投入量，可以用各个方案的投入量的平均值代表合理的投入量，即

1.3 激励的效用

设效用函数为U(x)，由于激励的方向不一致，因此采用归一化的“S”型效用函数:

其中a、b为风险系数。可以定义，当激励为1时，效用值为 0.9;激励为 0时，效用为 0.5。即U(1)=0.9，U(0)=0.5。代入式(3)，可以求出:a=1，b=2.2。那么效用值就代表了决策者对于激励为p时的偏好程度。可以看出在效用值0.5附近，不论正向激励还是负向激励的微小改变都将对效用值产生较大的影响，这符合人们风险厌恶的心理。

2 激励效用理想解法

2.1 决策矩阵

设有m个方案n个决策属性指标构成的矩阵X=(xij)m×n称为决策矩阵。应该注意，决策属性指标根据指标变化方向，大致分为3类:效益型(正向)指标、成本型(逆向)和中间型指标。效益型(正向)指标具有越大越优的性质，成本型(逆向)指标具有越小越优的性质，中间型指标具有越靠近理想值越优的性质。

2.2 决策矩阵的激励化

在决策矩阵X=(xij)m×n中，根据决策属性指标的类型，利用式(2)计算相应的激励指标:

1)对于正向指标fj，取则:pij=

2)对于逆向指标fj，取则:pij=

3)对于中间型指标fj，取¯x=理想值，则:

矩阵 P=(pij)m×n称为激励化矩阵，变换后pij∈(－∞，+∞)，正向指标、逆向指标及中间型指标均被转化为正向指标。

2.3 激励效用矩阵

将激励化矩阵 P=(pij)m×n代入式(3)，进行效用化。

得到效用化矩阵 Y=(yij)m×n，满足 0≤yij≤1，且是正向指标，最优值是1，最劣值是0。

2.4 各指标权重的确定

确定属性权重的方法［4］可分为主观赋权法、客观赋权法两大类。主观赋权法如专家调查法、标定系数法、AHP法等，是根据决策者主观偏好信息间接或决策者根据经验直接给出属性权重。客观赋权法如熵权法、主成分分析法、多目标优化方法等，是根据决策矩阵信息，通过一定的数学模型计算出。记得出的权重为:

其中ωj表示第j个指标的权重。由此可以得到加权激励效用矩阵

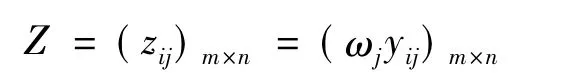
2.5 系统的理想解

很显然，理想及逆理想效用为

其中:yj+为第j个指标的理想效用;yj－为第j个指标的最不理想效用。所以加权激励效用矩阵的理想及逆理想方案分别为

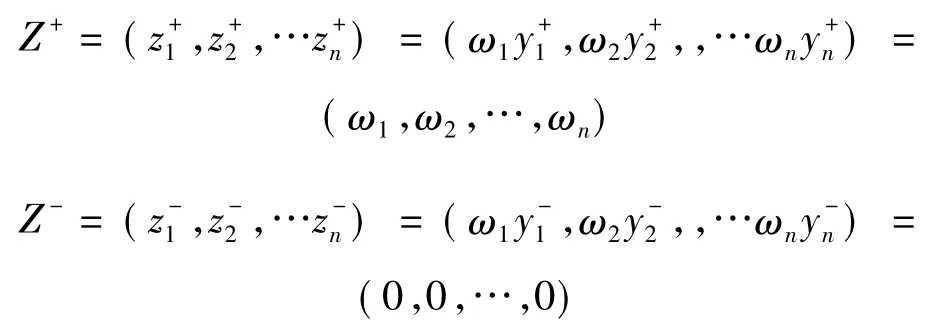
2.6 各方案到理想及逆理想方案的距离

设系统i到理想系统Z+和到逆理想系统Z－的距离为Di+、Di－，则:

2.7 相对贴近度并排序

3 实例分析

假设某系统的配置有7种配置方案［5］，如表1所示，利用基于激励效用的理想解法对7种配置方案的系统效能、费用、生命力、适应性、兼容性等指标进行综合比较，得出最优的配置方案。

表1 各配置费方案的指标值及各指标值的权重

在决策指标中，f1、f4、f5、f6是正向指标，f2、f3是逆向指标。由AHP法得到各指标权重:W=(0.4 0.14 0.1 0.13 0.08 0.15)T。利用激励化准则及式(4)得到激励化效用矩阵:

计算各方案的相对贴近度:U+=(0.549 0.654 0.393 0.384 0.510 0.41 0.568)，各个方案的排序结果为:X2＞X7＞X1＞X5＞X6＞X3＞X4。由排序结果知，决策者应该采用方案X2进行炮兵系统的配置，与参考文献［5］中的结果一致。然而，对加权效用矩阵Z=(zij)m×n各行求和，按总效用的大小进行决策，结果为X7。可以看出，基于激励效用的理想解法不仅对传统的理想解法进行了改进，而且克服了多品质因素间的干扰，比直接加权求总效用的决策准则更加优秀。