磁流变液在平行圆盘间的挤压流动分析

路国平，邓国红

(重庆理工大学重庆汽车学院，重庆 400054)

磁流变液作为一种新型的智能材料，其流变特性随着外加磁场的变化会急剧的变化，其黏度和屈服应力可由外加磁场连续控制。基于这些特性设计出的磁流变器件具有响应速度快、能耗低、结构简单等优点，在汽车、航空、医疗等领域都有着广泛的应用前景。

磁流变液的工作模式有剪切［1－2］、压力驱动［3－4］和挤压3种。相比于剪切和驱动模式，挤压模式的流变特性更加复杂，其相关的理论和应用研究都比较少。Alireza等［5］的研究表明磁流变液在挤压模式下能产生很大的可控力，并首次发现了磁流变液的凝聚效应。Laun等［6］研究了具有滑移现象的牛顿流体和幂率流体的圆盘挤压流动特性。徐春晖［7］等研究了宾汉流体的挤压黏性力与平行刚性圆盘的滑移参数的关系。廖昌荣等［8］分析了基于圆盘挤压模式的磁流变阻尼器的工作特性。

本文引入了临界剪切应力，建立了新的边界滑移模型，充分考虑磁流变液的幂率特性，建立了新的挤压模型，并分析了磁流变液在圆盘挤压下的流动特性，得出了挤压力与滑移系数及幂率指数的关系，为磁流变液在挤压模式下的应用提供了理论依据。

1 理论模型的确立

1.1 挤压模型

磁流变液在圆盘间的挤压流动模型如图1所示，半径为R的2个平行的同轴圆盘，在挤压力作用下分别沿Z方向相向运动，并且挤压圆盘间的磁流变液。两盘间距为H(H=2h，且H≪R)。由于磁流变液可被认为是不可压缩的流体，所以流体质点的密度ρ在流动中保持不变，即流体的运动满足质量守恒定律。由雷诺输运方程，可得

连续方程可简化为▽·U=0，即

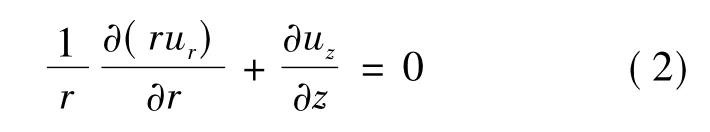
假设挤压速度U比较小，流动可假定为定常流动，挤压流问题可看作小雷诺数的蠕流问题。非定常项和对流项都是可忽略的高阶小量，而且z方向的压力梯度为零。则Navier-Stokes方程可近似为

对于磁流变液挤压流的本构关系的表达，原有的模型都忽略了它的剪切稀化或增稠现象。但清华大学的田煜等［5］用实验的手段发现了电磁流变液的剪切增稠现象，并讨论了这种幂率特性对电磁流变效应及机理的影响。本文在充分考虑了磁流变液的幂率特性的情况下，提出了新的挤压模型

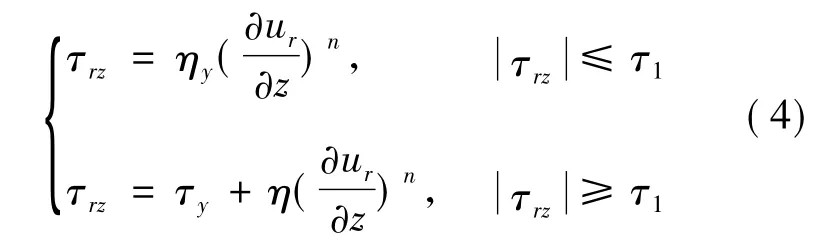
式中:τrz为剪切应力;n为幂率指数;τ1为屈服应力;τy为随磁场强度而变化的动态屈服应力为剪切应变率;η为磁流变液屈服时的黏度;ηy为磁流变液未屈服时的黏度，ηy比η约大102个数量级。

图1 磁流变液圆盘挤压流动模型

1.2 边界滑移条件

润滑理论引用了临界剪切应力来描述粘塑性流体的本构关系，并表明了当剪应力达到临界剪切应力时，其不再随剪应变率的变化而增加，且流体开始发生滑移［10］。磁流变液作为一种黏度可控的粘塑性流体，其边界滑移模型可表示为

式中:US为滑移速度;τL为临界剪切应力。

2 挤压流动分析

在柱坐标系(r，θ，z)，流场速度只有 Ur和 Uz两个分量［11］。由于磁场的不均匀性，流场屈服面与2个挤压面并不平行，而是与圆盘相交于r=Ro处。在求解过程中，可把流场分为2个区域［12］。如图1所示，阴影部分是2圆盘面，虚线为屈服面。在r＜Ro的区域，可把流场看作单一的以高黏度η(H)流动的牛顿流体，称之为牛顿区;在r＞Ro的区域，图中虚线包围的部分为双黏区，存在屈服面将流场分为屈服区和未屈服区。

2.1 径向速度和压力梯度的分布

在r＜Ro的区域，磁流变液可看作黏度很大的牛顿流体，利用流场的对称性，结合连续方程和挤压模型式(4)，在边界滑移条件下进行求解，可得到流场的径向速度

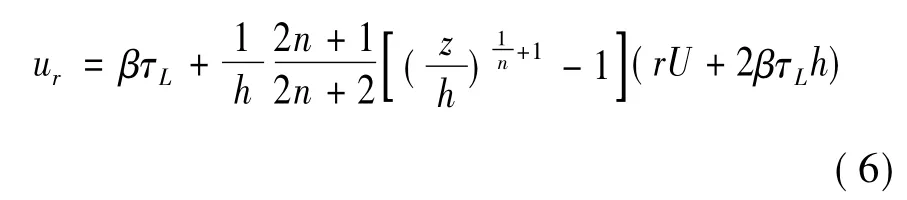
压力梯度为

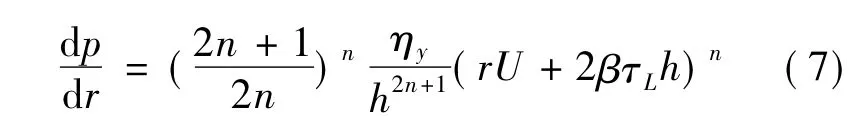
剪切应力为

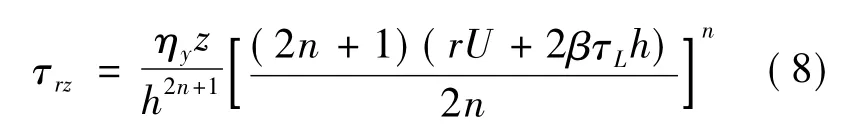
而在r=R0且Z=h时，磁流变液被屈服，此处τrz=τ1，据此可得屈服面与圆盘相交处

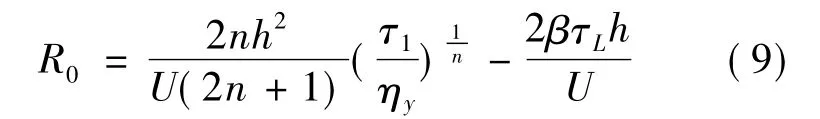
在r＞Ro的区域，由于流场的对称性，对式(3)积分得到 τrz=(dp/dr)z，而在屈服面上 τrz=τ1，则可知屈服面位置为

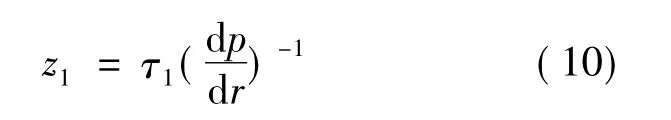
在0≤z≤z1的区域，磁流变液黏度较大，为未屈服区;而z1≤z≤h的区域为屈服区。利用流场的对称性，结合挤压模型，在边界滑移条件下计算得到流场在r＞Ro的径向速度分布:

由于流场速度在屈服面位置的连续性，将式(10)带入式(11)可得压力梯度的隐式表达式

由于实际流场中，压力梯度是随r的变大而递增的［7］，且在r＞Ro的区域，压力梯度是大于1的，所以式(12)中(dp/dr)－2是小量，可以忽略不计，故压力梯度可近似表达为

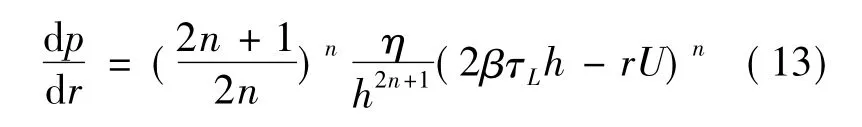
2.2 挤压力

根据以上计算结果，可知流场压力梯度的分布为

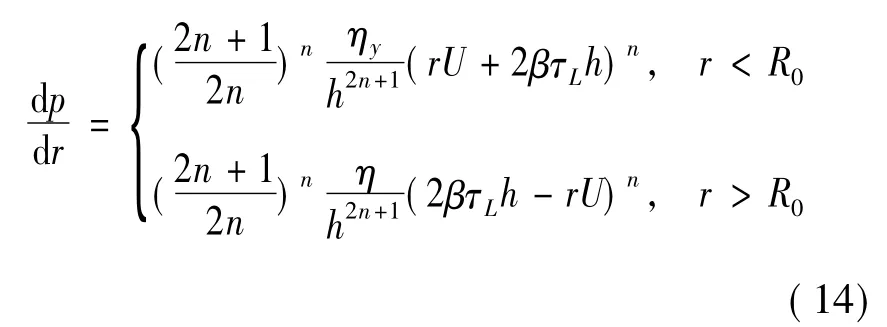
由于挤压力与压力梯度存在如下关系

将压力梯度式代入上式可得圆盘挤压力的表达:

3 结果讨论

圆盘挤压模型的参数取值:h=3 mm，R=40 mm，U=20 mm/s。选用磁流变液材料 MRF-132AD进行分析，其黏度η=0.06 Pa·s。本文不分析磁场强度的变化对流场的影响，故选取特定磁场下的情况进行分析。取磁场强度为H=200 kApm/m，此时 ηy=6 Pa·s，屈服应力 τ1=42 kPa。

3.1 速度场的分布特点

假设流体的滑移速度为US=βτL=2 mm/s，则屈服面与圆盘的径向交界R0=1.5 mm。在r小于1.5 N的区域，磁流变液接近于牛顿流体，取n=1进行分析。由于流场的对称性，本文只分析上半个流场，即z大于0的流场。图2所示为牛顿区的径向速度分布，由图可以看出:随着r的增大，径向速度增大，但由于流体的高黏性，流动非常缓慢，而且越靠近圆盘处流动越受阻，在z=2.5附近流动几乎停滞。但边界附近又开始有流动，这是由于边界处的滑移使得流体的润滑性增强。

图2 磁流变液在r＜1.5区域的径向速度分布

图3(a)和图3(b)显示了磁流变液在双黏度区径向速度分布的明显差异性。可以看出，屈服区的速度值明显大于未屈服区。未屈服区的速度分布比较平缓，近似于牛顿区;屈服区的速度在z方向近似于递减的线性关系，越靠近边界，速度越小。

图3 磁流变液在r＞1.5区域的径向速度分布

3.2 挤压力的分析

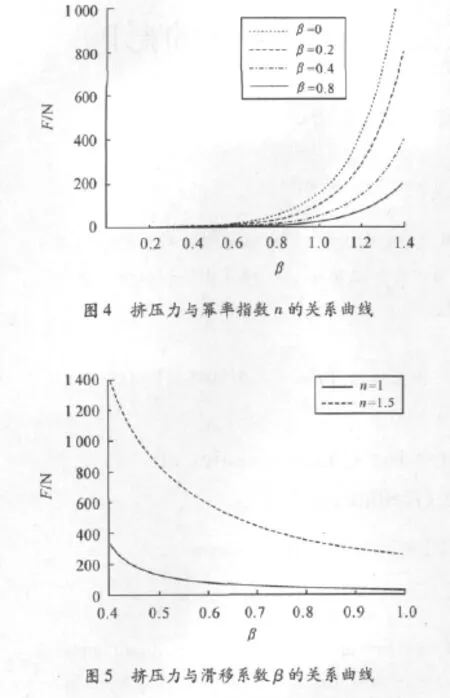
在圆盘挤压流的实际应用中，圆盘在不同的运动状态下挤压力的大小以及它与某些重要参数的关系都有着重要的意义。假设临界剪切应力为一定值，即取τL=10 kPa进行分析。图4和图5分别分析了幂率指数n和滑移系数β对挤压力的影响。

从图4可以看出，当n一定时，挤压力随着滑移系数的增大而变小。而当n增大时，挤压力不断增大。但当n小于1时，挤压力增大的幅度很小，挤压力受到的影响几乎可以忽略。当n大于1时，挤压力明显增大，且随n的增大而不断递增。这也验证了田煜等［5］发现的磁流变液的剪切增稠现象。由于n小于1时，其对挤压力的影响很小。图5只取了n=1和n=1.5两个值进行分析。可以明显地看出，挤压力随着滑移系数的增大而变小。但在n=1时，挤压力大小的变化很平坦，而n=1.5时，挤压力的大小变化幅度很大。

4 结束语

在原有的双黏度模型基础上，考虑了磁流变液的幂率特性和边界滑移，建立了新的挤压模型，将流场分为牛顿区和双黏区，得到了磁流变液在圆盘间的径向速度和挤压力的表达式。通过对圆盘间流场的分析可以看出，屈服区与未屈服区的径向流动差异很大，边界滑移对流场的影响也不可忽视。而幂率指数大于1后，其对挤压力的影响比较明显，即磁流变液的剪切增稠现象较明显。为了完善磁流变液的挤压理论，还应在磁场强度和临界剪切应力对速度分布和挤压力的影响上进行深入讨论和实验对比。

［1］Huang J，Zhang J Q，Yang Y，et al.Analysis and design of a cylindrical magneto-rheological fluid brake［J］.JournalofMaterials Processing Technology，2002(129):559－562.

［2］贺建民，黄金，钟银辉.磁流变液在圆筒间的粘塑性流动［J］.功能材料，2006，37(6):992 －993.

［3］He J M，Huang J，Fu L J.Design Analysis of Magnetorheological Dampers［J］.Proc SPIE，The International Society for Optical Engineering，2006，6040:475 －480.

［4］Jin Huang，Song Chen，Ping Wang.Analysis and Design of a Cylindrical MR Valve［J］.Advanced Materials Research，2011，197 －198:265 －268.

［5］Alireza Farjoud，Ryan Cavey，Mehdi Ahmadian，et al.Magneto-rheological fluid behavior in squeeze mode［J］.Journial of Smart Materials And Structures，2009，18:1－7.

［6］Laun H M，Rady M，Hassager O.Analytical Solutions for Squeeze Flow with Partial Wall Ship［J］.Journal of Non2 Newtonian Fluid Mechanics，1999，81(1/2):1－15.

［7］徐春晖，黄文彬，徐泳.平行刚性圆盘间有壁面滑移宾汉流体的挤压流动［J］.中国农业大学学报，2003，8(2):7－10.

［8］廖昌荣，骆静，李锐，等.基于圆盘挤压模式的磁流变液阻尼器特性分析［J］.中国公路学报，2010，23(4):107－112.

［9］田煜，蒋继乐，孟永刚，等.电/磁流变液中的剪切增稠现象［C］//第七届全国液体和软物质物理学术会议摘要.西安:西北工业大学出版社，2010.

［10］温诗铸，黄平.摩擦学原理［M］.3版.北京:清华大学出版社，2008.

［11］麻建坐，贺建民，黄金.圆筒式磁流变离合器传动特性分析［J］.重庆理工大学学报:自然科学版，2009，23(3):24－28.

［12］杨士普，任玲，朱克勤.平行圆盘间电流变液的挤压流研究［J］.功能材料，2006，37(5):690 －696.