基于灰色强度偏好的冲突分析图模型
2019-11-21丁晨,康卫
丁 晨,康 卫
(阜阳师范大学信息工程学院,安徽阜阳236041)
冲突分析图模型(GMCR)理论由Kilgour等[1]首次提出,Fang等[2]对其进行了完整的描述,即冲突分析图模型法是以集合论和图论为方法论,通过对冲突行为进行定量和定性分析,使得冲突行为数学模型化,从而对冲突事态的过程和结果进行分析、预测,为决策者提供可实施的战略建议。由于图模型能为决策者提供简单、灵活、实用的模型结构以及合理的解决方案,所以被广泛应用于水资源冲突[3]、污染冲突[4]等领域。近年来,冲突分析图模型的研究主要集中在决策者偏好信息[5-9]、稳定性分析[10-12]、稳定后分析[13-14]等方面。现实中的很多冲突事件偏好信息往往是不全面的,为此,本文依据文献[9]提出的灰色偏好的冲突分析图模型理论框架,针对两个决策者灰色强度偏好及其稳定性进行分析研究。
1 图模型基本理论
冲突分析图模型用V ={N,S,G,P}表示,其中N(N ≥2)表示冲突事件中所有决策者组成的有限非空集合;S表示冲突事件中所有可行状态构成的非空集合,这里可行状态点是由每个决策者的策略选择进行组合而成;G表示冲突事件中决策者的状态转移情况;P表示冲突事件中决策者的偏好信息。
图模型解决实际冲突事件主要由建模、稳定性分析与稳定后分析3个阶段组成,而偏好的信息在中间发挥重要的作用。通常用相对偏好“≻”、等价偏好“~”和强度偏好表示决策者k对不同状态的偏好信息。例如,si,sj∈S 是冲突事件中的任意两个可行状态表示对于决策者k,状态si优于状态sj;表示对于决策者k,状态si等价于状态表示对于决策者k,状态si强烈优于状态sj。
定义1[1]决策者k ∈N,初始状态表示决策者k的所有弧集,称Rk为决策者k从初始状态s开始可以转移到的可行状态集合,记为Rk(s)=。
定义2[1]决策者k ∈N,初始状态,称为决策者k从初始状态s经过转移到达的单方面改进的可到达的状态集合,记为(s)=
定义3决策者k ∈N,初始状态,称为决策者k从初始状态s经过转移到达的单方面强改进可到达的状态集合,记为(s)=
2 灰色系统基本理论
灰色系统[15]能够有效处理模糊、不确定的信息,并能洞察系统的运行特征及其演化,能够开发、挖掘蕴含在系统观测数据中的重要信息,实现对现实世界的正确认识。通常把只知道取值范围而不知其确切值的数称为灰数(常用“⊗”表示)。在现实的冲突事件中,决策者个体理性受到信息不足、信息处理能力、时间等方面的限制无法作出一个完美或最优的解决方案,而灰数能有效处理不确定信息的性质,所以其适用于在高度不确定性的问题情境中进行决策分析,并为决策者提供合理的建议。
定义4[16]设为一般灰数,其中,对任意一个区间灰数且的下界和上界。
定义5[16]

3 灰色强度偏好的冲突分析图模型
当决策者在面临两种可选择的策略时,因个人偏好不同而具有不确定性策略选择,这种不确定性即为“灰色”,用灰数来表示。本节给出灰色强度偏好的定义,并定义灰色强度偏好下的稳定性概念。
定义6设S=表示可行状态集合分别表示在区间上 所 有 可 取 到 的 灰 数 的 集 合,状 态si,sj∈S,α ≥0,那 么 称为灰色偏好矩阵。其中,表示状态si优于sj的程度。
注1(1)如果(2)如果,那么状态si强 烈 优 于 状 态sj,记si>>sj;(3)如 果那 么 状 态sj一 般 优 于 状si,记sj>si;(4)如 果,那么状态si优于状态sj可能性小越小,则状态si优于状态sj可能性越小;(5)如果,那么状态si等价于状态sj,记si~sj;(6)如果,那么状态si优于状态sj可能性大,越大,则状态si优于状态sj可能性越大;(7)如果,那么状态si一般优于状态sj,记si>sj;(8)如果,那么状态sj强烈优于状态si,记
定义7设S表示可行状态集合,决策者k ∈N,状态表示对于决策者k,状态si优于状态sj偏好的程度,则决策者k 的灰色相对强度偏好矩阵为,其中,表示对于决策者k,状态si相对状态sj的灰色相对确定性偏好程度。
定义8[17]决策者k ∈N,状态si,sj表示对于策者k,状态si比状态sj的相对确定性偏好程度,则决策者k的预期偏好值满足:(1)如决策者k持悲观态度,则决策者k持乐观态度,则;(3)如决策者k持中立态度,则

定义9决策者k ∈N,状态表示对于决策者k,状态si优于状态s,那么称γk为决策者k的灰色偏好阈值。
注2灰色偏好阈值γk是用来判断决策者k是否满足从一个状态向另一个状态作单方面改良转移的数值。
定义10决策者,状态si,,si(s),γk满足APk(si,s)≥γk,称( )s 表示决策者k从状态s的灰色单方面改良可达状态的集合,记为
定义11(灰色强纳什稳定(GSNash))设N为决策者集合,S为可行状态集合,状态s ∈S,对于决策者p ∈N,如果状态s满足R+p,γp(s =φ),则状态s是决策者p的灰色强Nash稳定。
定义12(灰色强一般超理性稳定(GSGMR)))设N 为决策者集合,S 为可行状态集合,决策者p ∈N,状 态s ∈S,如 果 对 于 任 一 状 态s1(s),至 少 存 在 一 个 状 态s2,使 得APp,则状态s是决策者p的灰色强GMR稳定。
定义13(灰色强对称超理性稳定(GSSMR))设N为决策者集合,S为可行状态集合,决策者p ∈N,状态s ∈S,如果对于任一状态s1,至少存在一个状态s2,对于决策者使得且至少存在一个状态对于决策者k ∈N,使得则状态s是决策者p的灰色强SMR稳定。
定义14(灰色强度序列稳定(GSSEQ))设N为决策者集合,S为可行状态集合,决策者p ∈N,状态,如果对于任一状态s1,至少存在一个状态s2,使得,则状态s是决策者p的灰色强SEQ稳定。
定义15(灰色弱一般超理性稳定(GWGMR))设N为决策者集合,S为可行状态集合,状态s ∈S,对于决策者p ∈N,若状态s是灰色一般的GMR稳定但不是灰色强GMR稳定,则状态s是决策者p的灰色弱GMR稳定。
定义16(灰色弱对称超理性稳定(GWSMR))设N为决策者集合,S为可行状态集合,状态s ∈S,对于决策者p ∈N,若s是灰色一般的SMR稳定但不是灰色强SMR稳定,则状态s是决策者p的灰色弱SMR稳定。
定义17(灰色弱序列稳定(GWSEQ))设N为决策者集合,S为可行状态集合,状态s ∈S,对于决策者p ∈N,若s是灰色一般的SEQ稳定但不是灰色强SEQ稳定,则状态s是决策者p的灰色弱SEQ稳定。
4 案例分析
利用“可持续发展”[9]的冲突事件来阐述灰色强度偏好GMCR框架在实际冲突事件中的可行性和适用性。在可持续发展的冲突事件中涉及两个决策者:环保机构(D1),开发商(D2)。环保机构有两个策略:强监督和弱监督;企业也有两个策略:可持续和不可持续。该冲突事件中涉及的决策双方共有4种策略选择,每个决策者对于一种策略都有选择(“Y”)或者不选择(“N”)两种态度,所有决策者都选择一种策略后形成的局势称为状态,如表1所示。

表1 “可持续发展”冲突事件的可行状态
根据表1,可用图1 来描述决策者的状态转移,图1 圆圈内字母表示可行状态,弧的箭头方向表示从一个状态转移到另一个状态,双向箭头表示状态之间转移是可逆的,实线表示D1状态转移情况,虚线表示D2状态转移情况。
假设开发商环保具有一定的责任,由于该冲突事件中环保机构和开发商对待可行状态的偏好均具有不确定性,所以可对冲突事件中的决策双方的可行状态采用两两比较,并用灰数表示决策者对不同可行状态相对偏好的不确定程度,如表2所示。

图1 决策者状态转移图
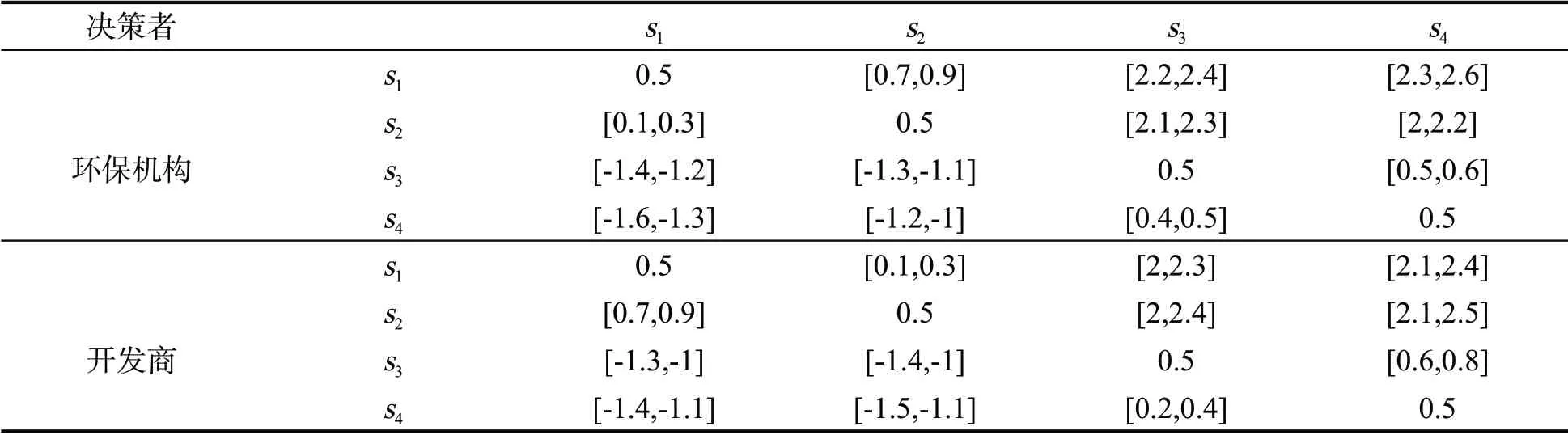
表2 环保机构和企业的灰色强度偏好矩阵

表3 环保机构和企业的灰色强度相对偏好矩阵
假设该冲突事件中环保机构和开发商对待冲突均保持中立的态度,且灰色阈值分为(1)γ1=0.1,γ2= 0.4;(2)γ1=0.6,γ2=1两种情况来讨论。当两位决策者灰色偏好阈值为第(1)种情形时,由灰色一般稳定性定义以及灰色强度稳定性定义可知,环保机构和开发商在冲突中的稳定性结果,如表4所示。表4中“√”表示在某种稳定性定义下某个可行状态是稳定的;如果一个状态中所有决策者在某个稳定性定义都是稳定的,那么称该状态为稳定性下的均衡解(Equilibrium),用“E”表示,对应位置用“*”标注。类似地,可以给出环保机构和开发商的灰色偏好阈值为第(2)种情形时的稳定性结果,如表5所示。

表4 γ1 =0.1,γ2 =0.4时,可持续发展冲突事件稳定性分析结果

表5 γ1 =0.6,γ2 =1时,可持续发展冲突事件稳定性分析结果
由表4和表5可知,在给出的两种不同灰色偏好阈值情形下,如果采用灰色一般稳定性进行分析,状态s1满足可持续发展冲突事件的均衡解,即环保机构选择强监督、开发商维持可持续发展,这也是可持续发展事件冲突解决的常见结果。当环保机构的偏好阈值由0.1增至0.6时,对环保机构而言,状态s4在GGNash、GGGMR、GGSMR、GGSEQ稳定性定义下是稳定的;与此同时,开发商的偏好阈值由0.4增至1时,任何状态均不满足灰色一般稳定性定义。除此之外,无论灰色偏好阈值处于哪种情形下,对于环保机构和开发商而言,状态s2均满足GSGMR、GSSMR稳定性以及GGGMR、GGSMR稳定,这使得在可持续发展冲突事件中,当开发商选择可持续发展的策略时,环保机构更有充足的理由作出弱监督的策略选择,且这样的选择更符合实际冲突事件的解决方案。
