带有交叉杠杆的多元随机波动率模型
2011-06-02孟昭为
刘 鑫,孟昭为
(山东理工大学理学院 ,山东淄博 255049)
在金融时间序列中,一元SV模型对时变方差的研究已经相当的成熟,把这些模型推广到多元SV模型,研究分析多元金融时间序列的相关结构,然后把它们应用于投资组合的优化、风险管理以及衍生性商品定价等方面已成为现代计量经济学最为关注的问题之一。对随机波动率模型的多元因子建模,已经广泛应用到对高维股票收益数据的复杂动态结构分析中。另一方面,在目前的文献中,对带有交叉杠杆效应的MSV模型的有效估计方法(或者非对称性)的研究还很少。
本文研究的是一个带有交叉杠杆效应的广义MSV模型,并利用多步移动抽样,提出了一个新的有效的MCMC算法。对SV模型运用MCMC方法,关键是从它们的完全条件后验分布中有效地抽取潜在的波动变量的样本。对一元波动变量来说在其他时刻的波动变量和其他参数给定的条件下,这一时刻的波动变量用单步移动抽样很容易获得。这就表示当用单步移动抽样时,要多次重复使用MCMC算法进行抽样,以获得准确的估计。因此,本文依据近似线性高斯状态空间模型提出了一个快速、有效的状态抽样算法。
1 带有交叉杠杆效应的MSV模型
1.1 MSV模型的基本形式
一元杠杆SV模型的基本形式为

其中:

其中:yt表示在t时刻的股票收益;αt是对数波动的潜在变量;Nm(μ,Σ)是均值为μ,协方差阵为Σ的m维正态分布,把它扩展到MSV模型上时,令yt= ( y1t,…,ypt)'表示 P维股票收益向量;αt=(α1t,…,αpt)'表示它们相应的对数波动向量。
MSV模型的基本形式可以表示为

其中

Σ0第(i,j)个元素表示Σηη的第(i,j)个元素除以1 -φiφj,且满足稳定条件

使得
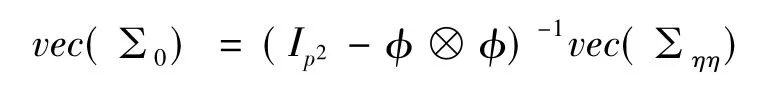
对可识别的过程,αt的预测值可视为0。
令

其中
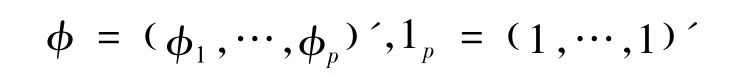
则MSV模型(1)~(4)的似然函数可表示为:
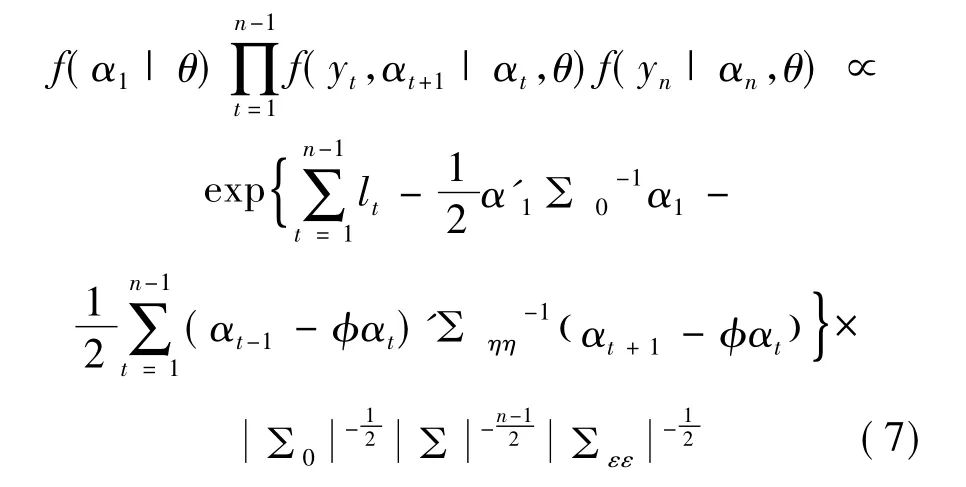
其中:

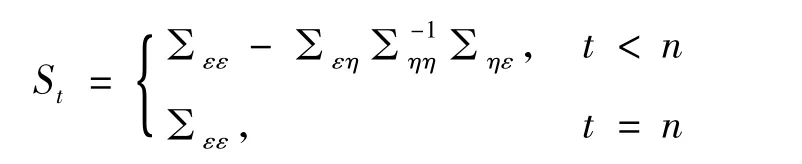
1.2 MCMC 方法
因为模型中含有很多的潜在变量αt,所以用它们去评估θ的似然函数或者一个高维的数值积分是非常困难的。本文通过贝叶斯方法,采用了模拟方法、MCMC方法,从后验分布中抽取样本,对模型中的参数进行统计推断。
对θ的先验分布,假设,
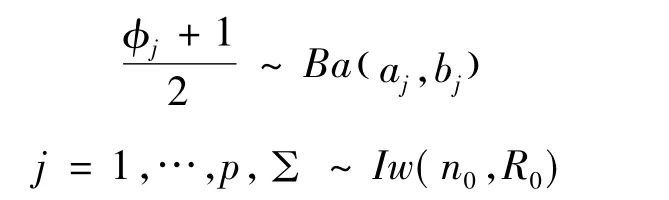
其中 Ba(aj,bj)和 IW(n0,R0)分别表示 Beta 分布和逆Wishart分布。
概率密度函数分别为
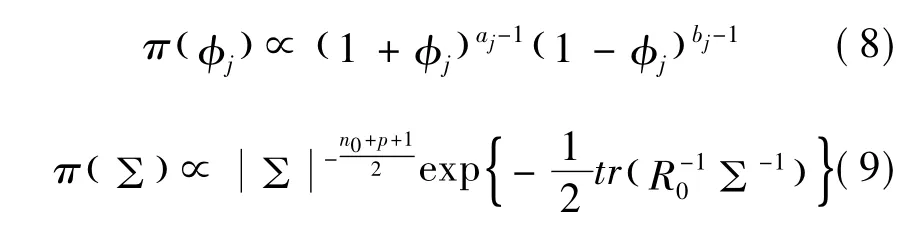
用方程(7)~(9),在

的条件下,θ,()α的联合后验密度函数为
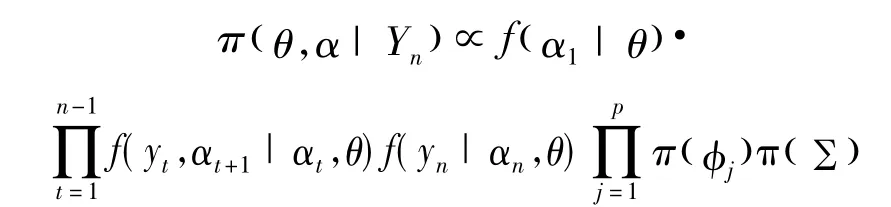
其中
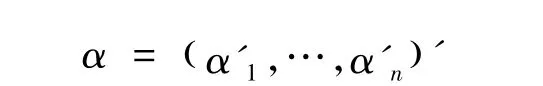
把MCMC算法分成3步:
① 生成 α|φ,Σ,Yn;
② 生成Σ|φ,α,Yn;
③ 生成 φ|Σ,α,Yn。
在第①步中,可用2种方法从α的条件后验分布中抽取它的样本:一是单步移动抽样,也就是t时刻,在其他时刻αj给定的条件下,抽取αt的样本;二是多步移动抽样,也就是在其他状态变量为条件的情况下,一段一段地抽取状态向量(αt,…,αt+k)的样本。
生成α:首先把
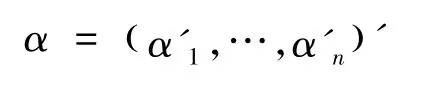
分为K+1段
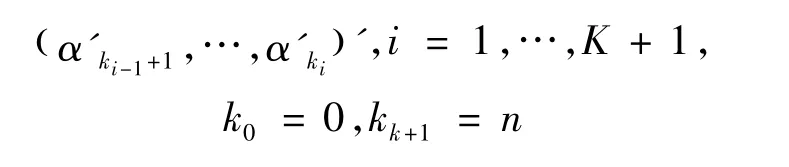
且

k的节点

是由
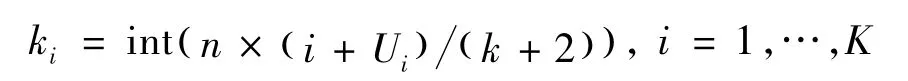
随机生成,其中Ui是在均匀分布U(0,1)上产生的独立随机变量。这些随机节点有一个优势就是通过调节这些点去改变MCMC迭代的方式。这里k是一个调整参数,以获得较少自相关的MCMC样本。
在第 i组假设 ki-1=s,ki=s+m,考虑在其它状态向量和参数条件的情况下,从它的条件后验分布中进行抽样,令

其中矩阵Rt表示当
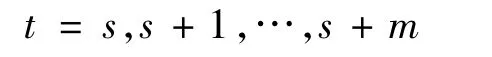
时,
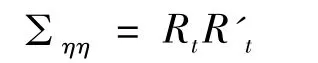
的一个choleski分解,且当
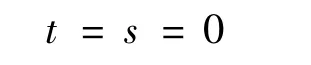
时,
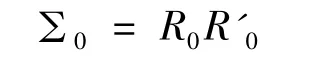
为了对MH算法构造一个合适的分布,本研究着眼于扰动项

的分布,因为它可以派生出


其中

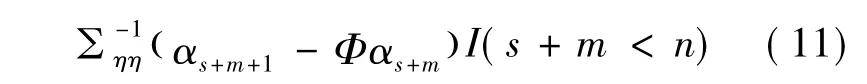
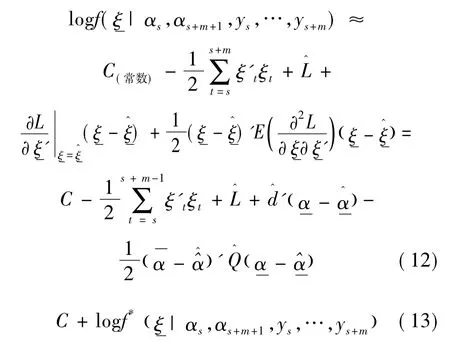
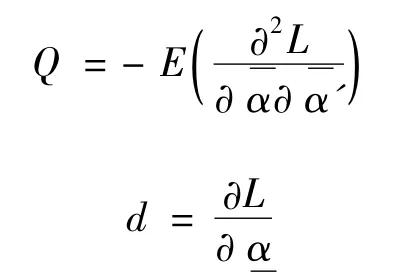
注意:Q是正定、可逆的。但是当m很大时,为求得mp个变量的多元正态分布的协方差阵,而必须求mp×mp阶Hessian阵的逆,这需要花费很长的时间。为解决这一困难,笔者解释方程(13)为来自一个辅助状态空间的后验概率密度函数,这样仅需通过卡尔曼滤波和平稳扰动项求出p×p阶矩阵的逆就行了。可以证明,f*是的后验概率密度函数,可以从下面的状态空间模型获得:
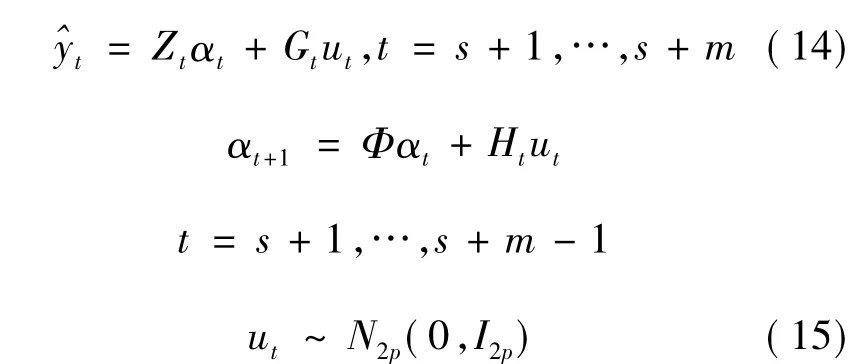

②通过式(14)和(15)得到近似线性高斯状态空间模型。
③在第2步把平滑扰动项应用于近似线性高斯状态空间模型,计算后验模式ξ^。
因此,这些步骤相当于用得分的方法去求条件后验分布密度最大化。作为的一个初始值当前的样本可以应用到MCMC方法中。如果近似线性高斯状态空间模型可以通过模式获得,则可以通过MH算法,从条件后验分布抽取ξ的一个样本,步骤:
1)建议用舍选法从
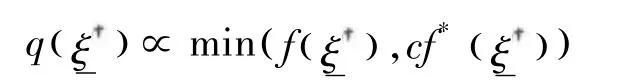
②以概率
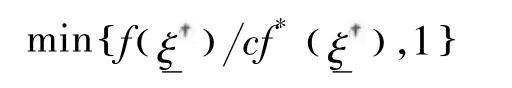
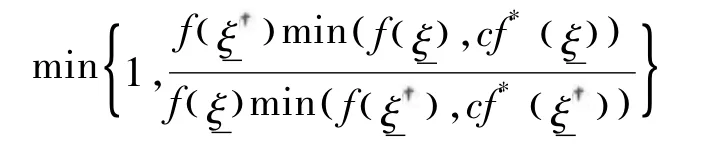
2)生成Σ和φ。有关Σ和φ的抽样方法非常直接。
生成Σ:
生成Σ的条件后验概率密度函数为
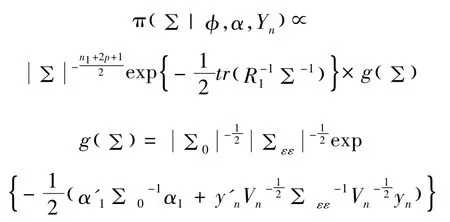
其中

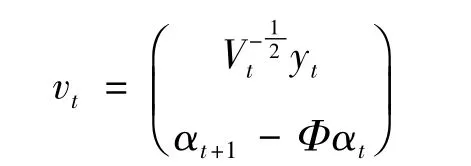
然后用MH算法,选定一个候选值
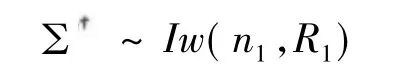
并且以概率
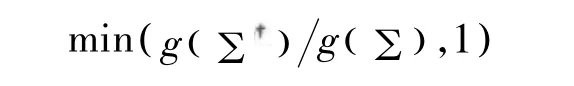
接受。
生成φ:
令Σjj为 p×p阶矩阵且为Σ-1的第(i,j)块,进一步令
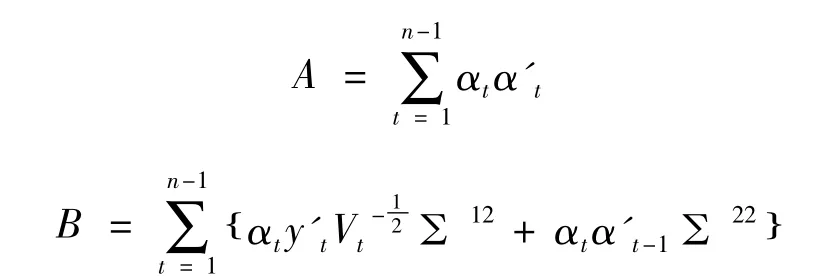
b为一个向量,且它的第i个元素相当于B的第(i,j)个元素,则φ的条件后验密度函数为:
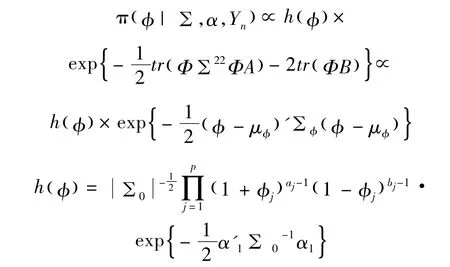
其中

⊙表示Hadamard积。用MH算法从φ的条件后验分布密度函数中抽取φ的样本,在R的截尾正态分布上生成候选值

且以概率
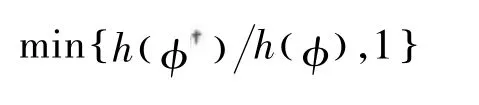
接受。
2 结束语
本文主要是对交叉杠杆MSV模型的潜在波动向量用多步移动抽样的方法提出一种有效的MCMC算法。为了抽取一组状态向量的样本,对目标似然函数的对数形式用泰勒展开,构造一个基于近似正态分布的MH算法。
[1]SO M K P,CHOI C Y.A threshold factor multivariate stochastic volatility model[J].Journal of Forecasting,2009,28(8):712 -735.
[2]TAKAHASHI M,OMORI Y,WATANABE T.Estimating stochastic volatility[J].Computational Statistics and Data Analysis,2009,53(6):2404 -2126.
[3]KOOPMAN S J.Disturbance smoother for state space models[J].Biometrika,1993,80:117 -126.
[4]CHIB S,NARDARI F,SHEPHARD N.Analysis of high dimensional multivariate stochastic volatility models[J].Journal of Econometrics,2006,134:341 -371.
[5]CHIB S,OMORI Y,ASAI M.Multivariate stochastic volatility[C]//Handbook of Financial Time Series.[S.l.]:[s.n.],2003:365 -400.
[6]利锋,张世英,何信.厚尾SV模型的贝叶斯分析及应用研究[J].西北农林科技大学学报:社会科学版,2003,3(6):88 -92.
[7]瑞锋.金融市场协同波动溢出分析及实证研究[J].数量经济技术经济研究,2006.23(10):141-149.
[8]陈泽忠,杨启智,胡金泉.中国股票市场的波动性研究-EGARCH-M模型的应用[J].决策借鉴,2000(5):66-69.
