距离频率ML方法无模糊估计动目标径向速度
2014-07-25张学攀廖桂生朱圣棋高永婵
张学攀,廖桂生,朱圣棋,高永婵,杨 东
(西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)
距离频率ML方法无模糊估计动目标径向速度
张学攀,廖桂生,朱圣棋,高永婵,杨 东
(西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)
在合成孔径雷达 地面动目标检测系统中,需要无模糊地估计运动目标的径向速度.当径向速度接近最大不模糊速度时,传统多通道最大似然方法的估计性能下降.针对以上问题,提出一种基于距离频率干涉相位的最大似然估计方法.相较于传统方法,所提方法有效地降低了概率密度函数扩散的影响,当径向速度接近最大不模糊速度时能够实现准确估计.从相关系数和干涉相位两个方面分析了噪声对径向速度估计的影响机理,并通过增加独立样本来减小噪声的影响.
合成孔径雷达;地面动目标检测;径向速度无模糊估计;最大似然估计;距离频率干涉相位
最大似然(ML)估计是一种从随机观测中估计确定参数的方法[8-9],可用于估计运动目标的加速度[10]和多普勒雷达网络中的矢量速度[11].将最大似然估计方法与多通道合成孔径雷达系统相结合,可以无模糊地估计运动目标的径向速度[12-13].最大似然方法利用多个独立不相关样本估计参数,估计精度随独立样本个数增加而提高[14].传统的多通道最大似然方法通过多基线或多载频[12]构造干涉相位关于径向速度的多个独立样本,从而实现径向速度的无模糊估计.但这两种方法不仅增加了系统的实现成本和复杂度[15],而且由于构造的干涉相位独立样本较少,使得估计精度受到较大限制.通过多视处理,可以得到较多的独立样本,但是需要折中考虑参数估计性能和分辨率[14].另外,对于传统最大似然估计方法,当径向速度接近最大不模糊速度时,干涉相位的概率密度函数扩散,致使径向速度的估计性能下降[12].
针对以上问题,笔者提出一种基于距离频率干涉相位的最大似然估计方法.该方法在距离频率域得到多个干涉相位的独立样本,通过增加独立样本来减弱概率密度函数扩散的影响,使得在径向速度接近最大不模糊速度时仍然可以准确地估计径向速度.
1 问题提出
在沿航迹干涉(ATI)系统中,动目标干涉相位φv与动目标径向速度Vr的关系为[12]

其中,<·>2π表示关于2π缠绕,b为基线长度,λ为载波中心频率对应的波长,平台速度为V.干涉相位对应的最大不模糊速度为

当地面运动目标的径向速度超过最大不模糊速度时,干涉相位出现缠绕问题,致使径向速度估计产生模糊,不能实现动目标的精确定位.运动目标干涉相位的概率密度函数[12]为
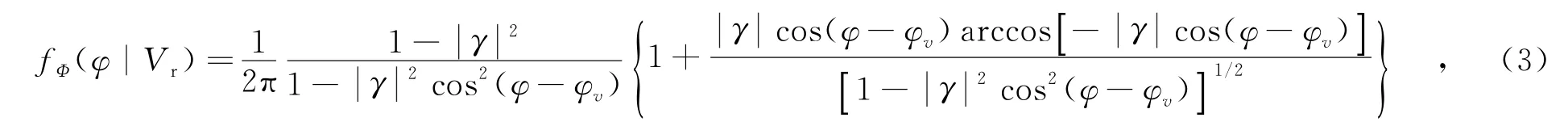
其中,干涉相位φ∈(-π,π],γ为两通道数据的相关系数.利用传统的多通道最大似然方法估计径向速度,即

似然函数L(Vr)为

其中,λm为第m个独立不相关干涉相位对应的波长,bn为第n个独立不相关干涉相位对应的基线长度,M和N分别为波长和基线个数.传统方法可以无模糊地估计径向速度,但是当径向速度接近最大不模糊速度时,干涉相位的概率密度函数扩散,致使径向速度的估计性能下降[12].另外,该方法利用多通道构造多个独立不相关的干涉相位,独立样本数量受到较大限制,需要折中考虑径向速度估计性能与系统实现成本和复杂度.所以,需要研究新算法改善最大似然估计方法的径向速度估计性能.
2 基于距离频率的最大似然估计径向速度方法
针对传统多通道估计方法面临的诸多问题,提出一种基于距离频率的最大似然估计径向速度的改进方法.该方法采用单载频双通道沿航迹干涉系统.首先,分别对两个通道的成像结果进行距离维傅里叶变换(FFT),得到相位与距离频率的关系,再利用干涉处理得到干涉相位关于距离频率的关系[16],即

其中,fc为载波中心频率,fr为距离频率,c为光速.将式(6)代入式(3),得到概率密度函数与径向速度和相关系数模值之间的理论关系式为

在通常情况下,两个通道成像后的信号是相关的窄带高斯过程[14],经过通带不交叠的线性时不变滤波器处理,不同距离频率对应的干涉相位之间是统计独立的.通过在距离频率域构造多个独立干涉相位与径向速度的关系,不仅降低了系统实现成本和复杂度,而且有效地增加了干涉相位独立样本个数.基于距离频率干涉相位的最大似然方法,运动目标径向速度估计为

其中,φk和frk分别为第k个独立不相关干涉相位及其对应的距离频率,K为独立样本个数.
文献[12]指出,当径向速度接近最大不模糊速度时,概率密度函数出现扩散(如图1所示,仿真参数如表1所示,如无特殊说明,后文均以表1参数仿真),导致最大似然估计性能下降.由图1可见,扩散问题主要表现在概率密度函数的形状上,其中心相位并没有改变.

表1 实测系统参数

图1 概率密度函数的扩散问题

图2对概率密度函数的影响
首先考虑概率密度函数扩散的原因.重新分析干涉相位概率密度函数的相关系数γ,假设相关系数与径向速度无关,则概率密度函数随径向速度和相关系数的变化关系如图2所示.当相关系数相同且较大时,不同径向速度对应的概率密度函数相同且无扩散问题;当径向速度相同但相关系数较小时,概率密度函数较小且出现扩散问题.由此可以得出结论:接近最大不模糊速度的径向速度通过改变相关系数导致概率密度函数出现扩散.
接下来,分析如何避免概率密度函数扩散.在最大似然方法应用背景下,给出干涉相位关于独立样本个数的概率密度函数为[17-18]


图3 K对概率密度函数的影响
概率密度函数随径向速度和独立样本个数的变化关系如图3所示.对比图3与图1可见,式(9)和式(3)的概率密度函数随径向速度的变化关系具有相同的形式,则可将式(9)用于分析独立样本个数对概率密度函数的影响.通过增加独立样本个数,可以有效地改善概率密度函数的扩散问题,即当径向速度接近最大不模糊速度时,可以通过增加独立样本个数提高径向速度的估计性能.
3 性能分析
本节着重分析噪声背景下的径向速度估计性能.通过上节分析可知,在最大似然估计方法中,相关系数模值和干涉相位对径向速度估计产生重大影响.首先分析信噪比对相关系数模值的影响.相关系数可以表示为[12]

其中,RSN表示信噪比,RSC表示信杂比,RCN表示杂噪比.

图4 信噪比对相关系数模值的影响
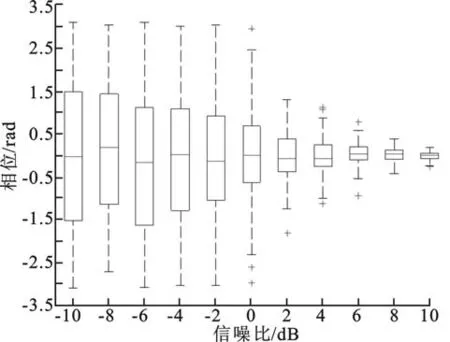
图5 不同信噪比情况下的相位分布
接下来,从相位方面分析噪声对径向速度估计的影响.在噪声背景下,运动目标干涉相位可以表示为
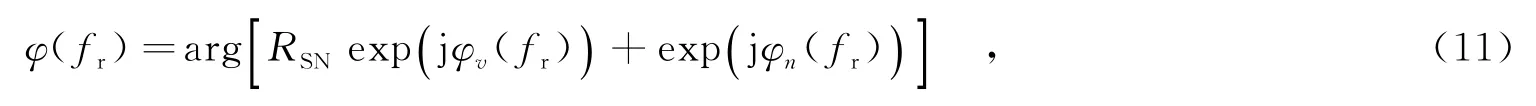
其中,φn(fr)表示不同距离频率单元的噪声相位,与距离频率fr无关,服从高斯分布.给出不同信噪比下,径向速度Vr=0时的相位分布盒图,如图5所示.由图5可见,当信噪比较小时,相位估计出现较大偏差,而且所估计的相位分布范围较大;随着信噪比的增加,相位估计更加准确,相位分布也更加集中.
由以上分析可知,噪声对相关系数模值和干涉相位均产生较大影响,导致不能准确估计径向速度.在50个独立样本时,经过100次蒙特卡洛实验仿真分析不同信噪比(RSN=0 d B,5 d B,10 d B)对似然函数的影响,如图6(a)~(c)所示,并在图6(d)中给出不同信噪比下的径向速度估计值.理论径向速度Vr=10 m/s,利用实测系统参数(表1)求得最大不模糊速度Vrmax=3.632 m/s.
由图6(a)~(c)可见,当信噪比较小时,理论径向速度对应的似然函数不一定是最大的.随着信噪比的增加,理论径向速度对应的似然函数值明显比其他模糊速度的似然函数值大,可以正确地估计出径向速度.由图6(d)可见,当信噪比较大(RSN≥5dB)时,所提方法可以准确地估计径向速度.当信噪比较小时,不能正确地估计径向速度,但基本分为两种情况:当-6dB≤RSN<5 d B时,径向速度估计值主要集中在模糊的径向速度附近,主要原因为,在该信噪比范围内,仍然以理论径向速度和模糊径向速度构成似然函数的较大值,由于噪声对干涉相位的影响,导致模糊径向速度对应的似然函数较大,使得径向速度估计出现模糊;当RSN<-6 d B时,径向速度估计值集中在(但不限于)模糊径向速度附近,其主要原因是由于信噪比较小,噪声对干涉相位的影响大于理论及模糊径向速度的影响,导致径向速度估计出现错误.
通过100次蒙特卡洛实验,仿真分析RSN=10dB时独立样本个数(K=1,100,500)对似然函数的影响,如图6(e)~(g)所示.当独立样本个数较小时,不能正确估计径向速度;随着独立样本个数的增加,理论径向速度对应的似然函数值明显大于其他似然函数值,因此可以正确地估计径向速度.

图6 信噪比和K对似然函数的影响
能否准确估计径向速度,主要取决于理论径向速度Vr0对应的似然函数是否是最大的.定义理论径向速度对应的似然函数值L(Vr0;fr,K)与最大似然函数Lmax(Vr;fr,K)的比值为R(称为径向速度似然比).通过径向速度似然比,可以判定利用最大似然估计方法估计的径向速度是否是理论的径向速度.以径向速度似然比为指标衡量独立样本个数K对径向速度估计性能的影响,仿真结果如图6(h)所示.由图6(h)可见,随着信噪比的减小,能够准确估计径向速度所需的最小样本个数逐渐增加.
以上结果说明,在噪声背景下,通过增加独立样本个数可以有效地提高径向速度似然比.其主要原因在于,当独立样本个数较小时,噪声相位对目标干涉相位的概率密度函数影响较大,导致径向速度估计出现错误;随着独立样本个数增加,服从高斯分布的噪声相位对干涉相位的影响越来越小,使得估计性能提升.
4 实测数据处理
通过实测数据处理估计运动目标的径向速度.实测系统参数如表1所示,对包含运动目标的场景进行实测数据接收,其中运动目标位于场景中的公路上.
合成孔径雷达成像结果如图7所示,公路上的运动目标由于具有较大的径向速度,在方位向偏移于合成孔径雷达图像中的公路.由径向速度Vr导致的定位偏移为

其中,ρa为合成孔径雷达成像的方位分辨率,在该系统下为2.4 m.

图7 合成孔径雷达成像及运动目标定位结果
利用所提方法估计图7中运动目标的径向速度.在距离频率域进行干涉处理,得到运动目标的干涉相位和相关系数模值如图8和图9所示.

图8 运动目标干涉相位
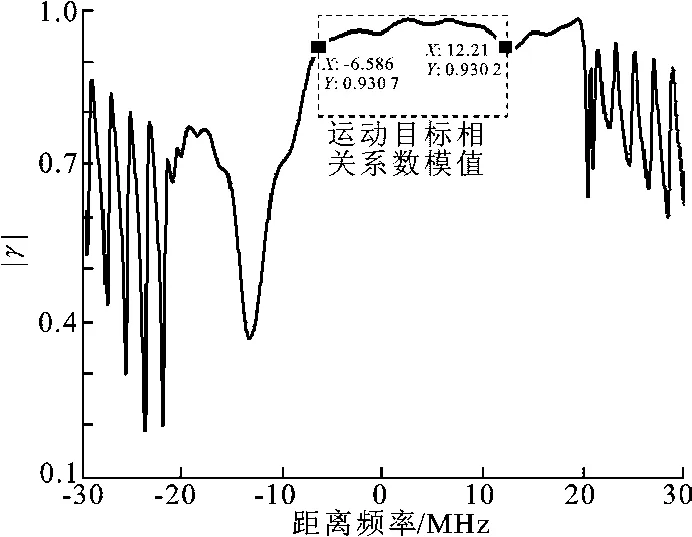
图9 运动目标相关系数模值
运动目标干涉相位随径向速度呈线性关系,与式(6)相符.运动目标的相关系数模值较大0.93),可以准确地估计径向速度.在Vr∈[-30 m/s,30 m/s]的范围内搜索待估计的径向速度,从而得到不同径向速度对应的似然函数,如图10所示.由此估计运动目标的径向速度=-6.1 m/s.为了验证所估计径向速度的准确性,利用式(12)对运动目标重新定位,方位偏差ΔX≈-191 m,定位结果如图7所示.
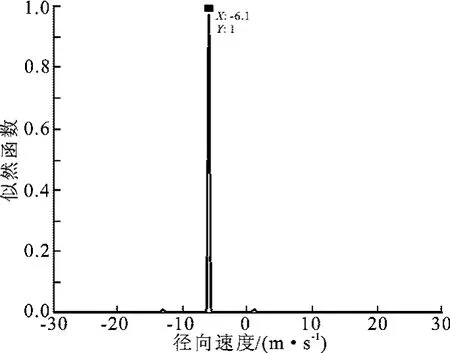
图10 运动目标径向速度估计
由定位结果可见,运动目标被定位于合成孔径雷达图像中的公路上.由此验证,利用所提方法可以准确地估计运动目标的径向速度.
5 总 结
笔者在距离频率域得到多个干涉相位和径向速度的独立样本,利用最大似然方法无模糊地估计地面运动目标的径向速度.所提方法通过增加独立样本减小概率密度函数扩散带来的影响,在径向速度接近最大不模糊速度时,仍具有较好的估计性能.笔者主要从相关系数和干涉相位两个方面分析了噪声对径向速度估计性能的影响,并通过增加独立样本减小噪声的影响.实测数据处理结果说明,所提方法具有较好的估计性能.相较于多基线或多载频等传统方法,所提方法有效地降低了实现成本和实现复杂度,可广泛应用于单载频双通道的沿航迹干涉合成孔径雷达系统.
[1]Bin G,Duc V,Lu Z X,et al.Ground Moving Target Indication via Multichannel Airborne SAR[J].IEEE Transactions on Geoscience and Remote Sensing,2011,49(10):3753-3764.
[2]Sun G,Xing M,Xia X G,et al.Robust Ground Moving-target Imaging Using Deramp-keystone Processing[J].IEEE Transactions on Geoscience and Remote Sensing,2013,51(2):966-982.
[3]Dragosevic M V,Burwash W,Chiu S.Detection and Estimation With RADARSAT-2 Moving-object Detection Experiment Modes[J].IEEE Transactions on Geoscience and Remote Sensing,2012,50(9):3527-3543.
[4]Zhu S,Liao G,Qu Y,et al.A New Slant-range Velocity Ambiguity Resolving Approach of Fast Moving Targets for SAR System[J].IEEE Transactions on Geoscience and Remote Sensing,2010,48(1):432-451.
[5]Xu R P,Zhang D D,Hu D H,et al.A Novel Motion Parameter Estimation Algorithm of Fast Moving Targets via Single-antenna Airborne SAR System[J].IEEE Geoscience and Remote Sensing Letters,2012,9(5):920-924.
[6]贺顺,杨志伟,徐青,等.分布式卫星SAR面目标径向速度估计方法[J].西安电子科技大学学报,2011,38(4):129-132.
He Shun,Yang Zhiwei,Xu Qing,et al.Radial Velocity Estimation for the Extended Moving Target with Distributed Slace-borne SAR[J].Journal of Xidian University,2011,38(4):129-132.
[7]杨垒,王彤,保铮.解运动目标径向速度模糊的一种新方法[J].西安电子科技大学学报,2009,36(2):189-192.
Yang Lei,Wang Tong,Bao Zheng.New Method for Solving the Ambiguity of the Radial Velocity of a Moving Target [J].Journal of Xidian University,2009,36(2):189-192.
[8]Monti G A,Tebaldini S.ML-Based Fringe-frequency Estimation for InSAR[J].IEEE Geoscience and Remote Sensing Letters,2010,7(1):136-140.
[9]Chung P J,Boehme J F.The Methodology of the Maximum Likelihood Approach:Estimation,Detection,and Exploration of Seismic Events[J].IEEE Signal Processing Magazine,2012,29(3):40-46.
[10]Ernst J M,Krogmeier J V,Bullock D M.Maximum-likelihood Acceleration Estimation From Existing Roadway Vehicle Detectors[J].IEEE Transactions on Intelligent Transportation Systems,2012,13(2):759-769.
[11]Insanic E,Siqueira P R.A Maximum Likelihood Approach to Estimation of Vector Velocity in Doppler Radar Networks [J].IEEE Transactions on Geoscience and Remote Sensing,2012,50(2):553-567.
[12]Budillon A,Pascazio V,Schirinzi G.Estimation of Radial Velocity of Moving Targets by Along-track Interferometric SAR Systems[J].IEEE Geoscience and Remote Sensing Letters,2008,5(3):349-353.
[13]Budillon A,Ferraiuolo G,Pascazio V,et al.Multi-channel SAR Interferometry via Classical and Bayesian Estimation Techniques[J].Journal on Applied Signal Processing,2005(20):3180-3193.
[14]Pascazio V,Schirinzi G.Multifrequency InSAR Height Reconstruction through Maximum Likelihood Estimation of Local Planes Parameters[J].IEEE Transactions on Image Processing,2002,11(12):1478-1489.
[15]Radius A,Marques P.A Study on the Radial Velocity Information Obtained from SAR Subapertures[C]//9th European Conference on Synthetic Aperture Radar.Piscataway:IEEE,2012:320-323.
[16]张学攀,廖桂生,朱圣棋,等.双通道距离频率干涉相位解运动目标径向速度模糊方法[J].宇航学报,2013,34(8): 1152-1158.
Zhang Xuepan,Liao Guisheng,Zhu Shengqi,et al.Radial Velocity Ambiguity Resolving Approach of Moving Targets Using Dual-channel Interferometric Phase of Range Frequency[J].Journal of Astronautics,2013,34(8):1152-1158.
[17]Gierull C H.Statistical Analysis of Multilook SAR Interferograms[J].IEEE Transactions on Geoscience and Remote Sensing,2004,42(4):691-701.
[18]Bamler R,Hartl P.Synthetic Aperture Radar Interferometry[J].Inverse Problems,1998,14(4):R1-R54.
(编辑:郭 华)
Unambiguous estimation of the radial velocity of a moving target by the range frequency maximum likelihood method
ZHANG Xuepan,LIAO Guisheng,ZHU Shengqi,
GAO Yongchan,YANG Dong (National Key Lab.of Radar Signal Processing,Xidian Univ.,Xi’an 710071,China)
The radial velocity of a moving target should be estimated unambiguously in the synthetic aperture radar-ground moving target detection system.Estimation performance of the conventional maximum likelihood method based on multi-channel would decline when the radial velocity approaches the maximum unambiguous velocity.To solve these problems,the ML estimation method based on the range frequency interferometric phase is proposed in this paper.Compared with the conventional method,the proposed method weakens the effect of probability density function spreading.The radial velocity can be estimated accurately even when it approaches the maximum unambiguous velocity.The effect of noise on radial velocity estimation is also analyzed from two aspects of correlation coefficient and interferometric phase,which can be reduced by increasing independent samples.Numerical and real data are processed to demonstrate the effectiveness of the proposed method.
synthetic aperture radar;ground moving targets indication;unambiguous radial velocity estimation;maximum likelihood method;range frequency interferometric phase
TN957
A
1001-2400(2014)05-0042-06
2013-05-26< class="emphasis_bold">网络出版时间:
时间:2014-01-12
国家973计划资助项目(2010CB731903);国家自然科学基金资助项目(61101249);长江学者和创新团队发展计划资助项目(IRT0954);西安电子科技大学研究生创新基金资助项目(JB142001-11)
张学攀(1986-),男,西安电子科技大学博士研究生,E-mail:xpzhang7@163.com.
http://www.cnki.net/kcms/doi/10.3969/j.issn.1001-2400.2014.05.008.html
10.3969/j.issn.1001-2400.2014.05.008
