二维市场上双寡头销售商间Stackelberg价格与选址竞争

张 晖， 周永务，2

(1.合肥工业大学管理学院，安徽合肥 230009;2.华南理工大学工商管理学院，广东广州 510641)

0 引 言

产品差异化问题可分为横向差异化与纵向差异化2类，纵向差异化涉及的是产品特性(如产品质量、大小等)的差异，而横向差异化产品在特性上并无差别，只是由于产品特性以外的因素引起的消费者偏好的差异。空间竞争问题属于横向差异化的范畴，处于不同地理位置的消费者购买商品时花费的距离成本有区别，从而导致消费者的偏好产生差异。空间竞争问题主要研究2个方面的内容:价格的确定与位置的选择。文献[1]提出空间竞争问题以后，此类问题就一直是学者们研究的热点，其研究内容按空间维数可以分为一维与多维两大类。

对空间竞争问题的研究大多关注一维情况。该类研究可以追溯到Hotelling开创性地提出了线性市场、线性距离成本下的两销售商选址“最小化”原则[1];文献[2]后来指出在Hotelling的假设条件下，“最小化”原则下的均衡价格并不存在。文献[3，4]指出均衡的存在与否在很大程度上依赖于具体的空间距离成本函数。文献[4]同时提出，当距离成本函数是二次的而非线性时，Hotelling模型中的纯战略价格均衡是存在的，且均衡位置在市场区间的两端，被称为“最大化”原则。随后，诸多学者对一维市场的空间竞争问题进行了深入研究[5-7]。国内学者也给予一维市场的空间竞争问题以足够的重视，如文献[8，9]扩展了Hotelling模型，研究了Stackelberg价格博弈下双寡头销售商的定价与选址策略。

在多维情况下，文献[10，11]得出了二维空间市场条件下双寡头销售商的位置应符合“最大-最小”原则，即在某一维度最大化产品差异，在另一维度最小化产品差异;文献[10]将Nash选址博弈与Stackelberg选址博弈进行了比较，得出Stackelberg选址博弈要优于Nash选址博弈。在三维或更高维的产品差异化问题研究上，文献[12]得出了类似的结果，即符合“最大-最小-最小”原则;文献[13]为二维市场模型添加了用以描述消费者偏好的异质性这一随机变量，以此来确定双寡头销售商的选址问题，并将其推广到更高维的情形。然而，对于采用Stackelberg价格博奕时销售商的均衡价格与均衡位置问题，有关文献很少。

本文主要研究在一个二维的矩形市场条件下，双寡头销售商间采用Stackelberg价格博弈时双方的最优定价与最优选址问题。按传统空间竞争问题研究方法，先讨论第2阶段的定价问题，再来分析第1阶段的均衡位置的确定问题，得出其均衡位置仍然遵循“最大-最小”原则的结论。在确定均衡位置后，本文接着来量化均衡价格，通过比较与文献[11]中的Bertrand-Nash均衡利润，得出Bertrand-Stackelberg博弈将使得双方的利润均优于采用Nash价格博弈时的利润，且作为追随者的一方能获得更大的利润。然后对均衡利润进行简单分析，揭示均衡利润与矩形市场边的长度的关系。最后，本文用数值实例来说明模型的应用。

1 Bertrand-Nash竞争模型

由文献[11]，Bertrand-Nash竞争模型下，消费者均匀分布在一个矩形区域，矩形的长为h单位，宽为1个单位。以该矩形的两邻边作为坐标轴建立直角坐标系，不妨以长为横轴，宽为纵轴。两销售商A和B在市场中的初始位置对称，且均可以对位置进行无成本的变动，以最大化各自的利润。A与B均无成本地销售某一同质商品，售价分别为p a和 p b，A的初始位置在该市场的左下角，B的初始位置在市场右上角与A对称的地方。此外，单位消费者单位时间内仅消费单位商品，且所有消费者的偏好相同，他们观察2个销售商各自的售价和自身到2个商店的空间距离成本，从而选择去总成本最小的商店购买商品。

分别用(a1，a2)与(b1，b2)来表示A与B的初始位置，则ai≤bi，i=1，2，且将到2个商店无差异的消费者的坐标设为(x1，x2)。无差异消费者(x1，x2)的轨迹表达式为:

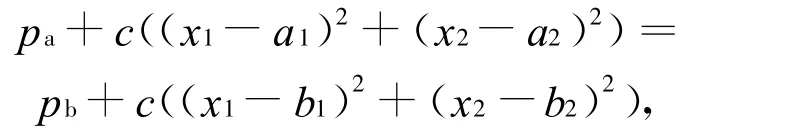
此式可简化为:

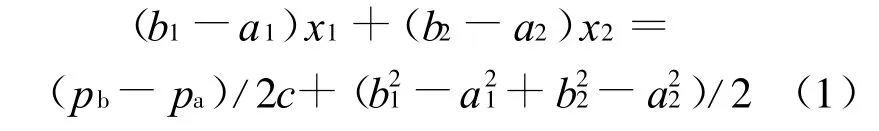
如图1所示，按寡头销售商的位置分为2部分来讨论。

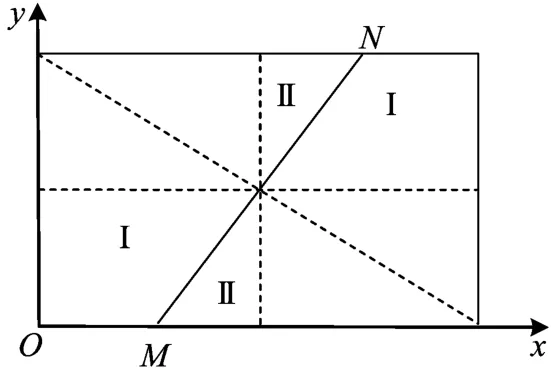
图1 二维市场上销售商初始位置分类

第1种情况即(b2-a2)/(b1-a1)＜h的情形，此时A与B的位置在图1中Ⅰ的区域(图1中矩形区域内的实线是矩形对角线的垂直平分线)，第2种情况是在图1中Ⅱ的位置，但分析过程类似。相对称的销售商的位置也有可能刚好处于直线MN上，但由于这只是小概率事件，因而，为了讨论的方便，可以忽略这种情况。这样，本文可以仅分析第1种情况，第2种可做类似处理，而且并不影响结论。由文献[11]，在Bertrand-Nash竞争的第1种情况下，两销售商的最优定价与最优利润分别为:

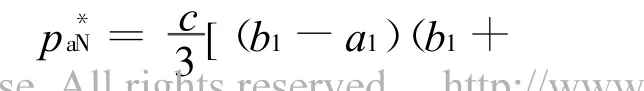
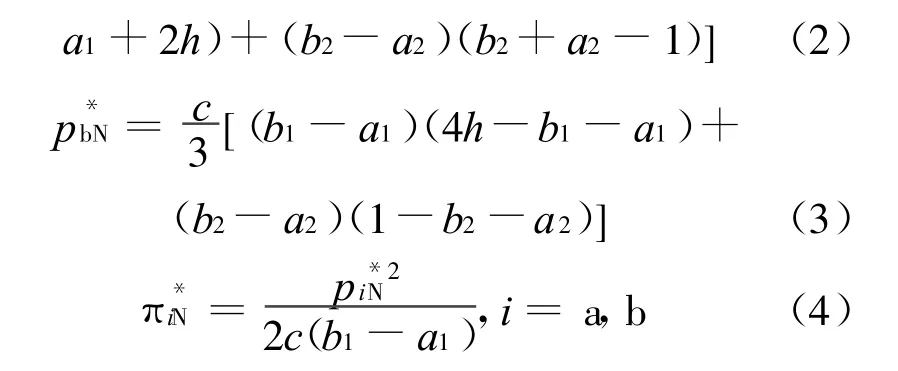
其中，下标N表示Bertrand-Nash的均衡结果。

2 Bertrand-Stackelberg竞争阶段分析

在假设的二维市场中，双寡头销售商的初始位置是给定的，且均可以无成本地调整自己的位置，以实现均衡利润。对销售商来说，第1步就是要确定均衡位置，这也是博弈的第1阶段，到博弈的第2阶段才是均衡价格的确定。然而，均衡位置的确定是依赖于均衡价格函数形式的，因此，分析上习惯于将博弈的2个阶段逆过来，先分析博弈的第2阶段——价格的竞争，再来分析博弈的第1阶段——均衡位置的确定，进而可得出均衡状态下双寡头销售商的价格、位置与利润。

2.1 价格的竞争

基本假设仍然与前面类似，A与B同时进入市场，处于相对称的位置。区别在于有一方先报价(不妨设为A，即A为领先者)，作为领先者的A知道追随者B将根据自己的报价来调整报价。A将B的反应函数代入自己的利润函数，从而确定自己的最优售价。B再根据A的最优售价来确定自己的最优售价，这是博弈的第2阶段，即以位置为参数的均衡价格的确定。

与前述类似，本文只讨论第1种情形，即(b2-a2)/(b1-a1)＜h的情形。

在第1种情形下，二维市场上无差异的消费者轨迹线截取市场边界线x2=0，x2=1的横坐标分别为 x1/0与x1/1，如图2所示(图中直线MN的斜率是h)。

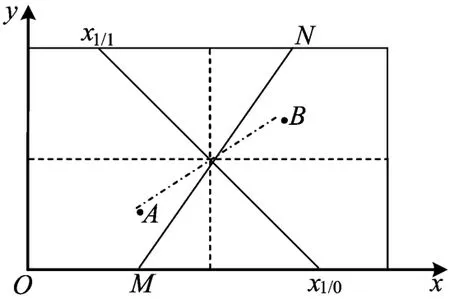
图2 二维市场竞争图示

x1/0与 x1/1的值分别为:

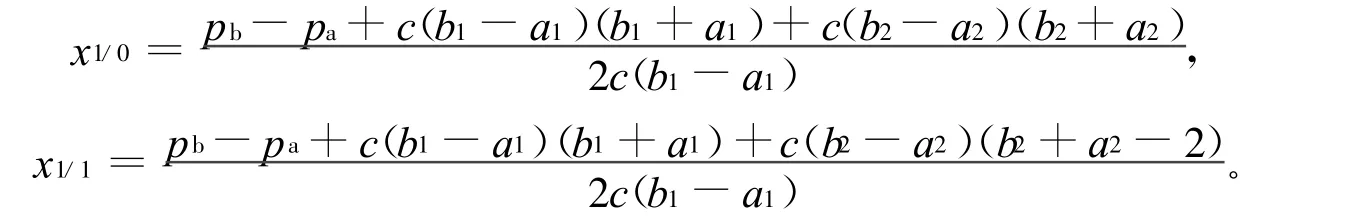
因此，A与B的市场份额分别为:

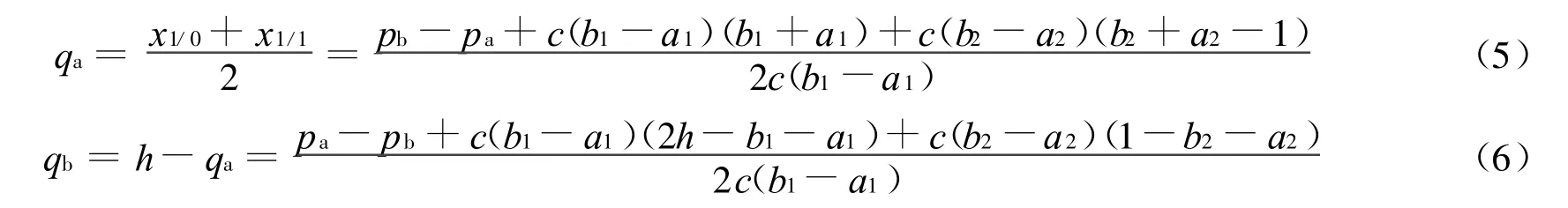
这样，B的利润函数可表示为:

类似可得A的利润函数。

易见，给定p a不变的情况下，πb是p b的凹函数。

由此，求(7)式的一阶条件，得出B关于A的反应函数(8)式，由于A知道B的该反应函数，经整理，可得A的利润函数(9)式，即

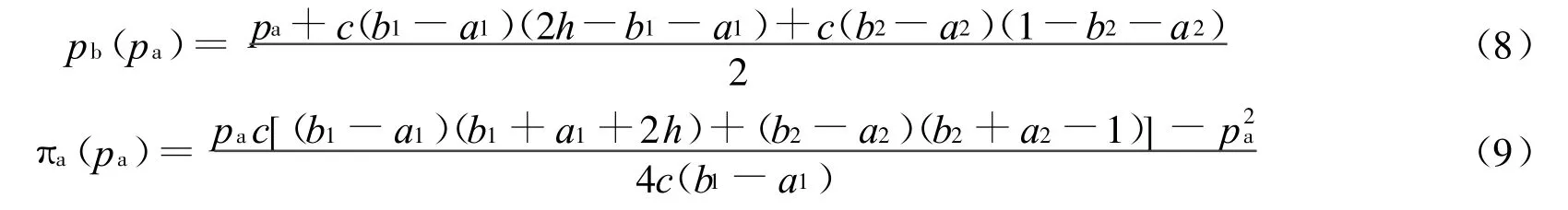
易知A的利润对其售价也是凹函数。因此对(9)式求一阶条件，得出A的最优定价为:

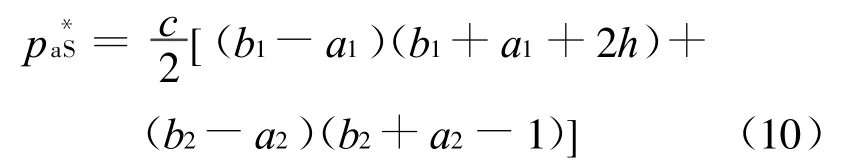
将(10)式代入(9)式，得出A的最优利润为:

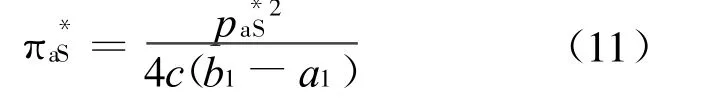
其中，下标S表示 Bertrand-Stacklberg的均衡结果。

将(10)式代入(8)式，可得追随者B的最优定价为:

再将(10)式与(12)式代入(7)式，得出B的最优利润为:

这样就确定了第2阶段的均衡价格与均衡利润关于位置的表达式。

2.2 均衡位置的确定

观察(13)式，分别对b1、b2求一阶偏导，可得其符号函数分别为:

由假设A、B对称，即有条件a1+b1=h，a2+ b2=1。又由b2＞1/2，可知:

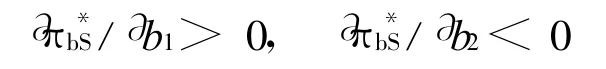
类似地，由A、B对称且a2＜1/2可得出:

由此可知，A的利润随着横坐标的增大而减少，随着纵坐标的增大而增加，而B的利润随横坐标的增大而增加，随纵坐标的增大而减少。这样，A与B的均衡位置分别在(0，1/2)与(h，1/2)处。于是，有下面结论:

结论1 在矩形市场中的Bertrand-Stackelberg博弈下，均衡位置同样会导致最大化某一维度差异，却最小化另一维度差异，即“最大-最小”原则在该博弈下仍然有效。

3 2种博弈下均衡利润的分析

将A与B的均衡位置代入对应的均衡利润表达式中，在Bertrand-Stackelberg博弈下，均衡状态时双寡头零售商的利润分别为:

而在Bertrand-Nash博弈下，对应的均衡状态时两者的利润为:

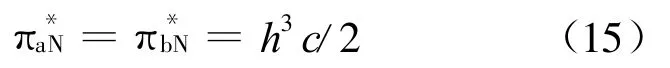
显然，有下面结论:

结论2 Bertrand-Stackelberg博弈下双方的最优利润要优于其在Bertrand-Nash博弈下的最优利润，且Bertrand-Stackelberg博弈下追随者的利润要严格高于领先者的利润，即追随者存在后发优势。具体来说，领先者的利润增长了1/8倍，追随者的利润增长了9/16倍。

结论2可以提供一些管理启示，即双寡头的零售商均有动机来执行Bertrand-Stackelberg博弈，尤其是作为追随者的角色来参与Bertrand-Stackelberg博弈。

此外，由(14)式、(15)式可知，不论是采用Bertrand-Nash博弈还是采用 Bertrand-Stackelberg博弈，均衡利润都对均衡位置所在矩形边的邻边长度呈3次方递增。而且，通过计算第2种情况可以发现，均衡利润对均衡位置所在边的长度呈线性递增关系。于是，有下面结论:

结论3 不论是采用Bertrand-Nash博弈，还是采用Bertrand-Stackelberg博弈，双寡头销售商的均衡利润都关于所在边的长度呈线性递增，关于其邻边长度呈3次方递增。

由结论3可知，扩大总的市场大小对双寡头的销售商来说都是有利的，尤其是当其商店位置相距较大时，继续扩大该距离能使双方攫取垄断利润的能力大大增加。

4 模型应用

小区通常是由主干道路或其它自然障碍物围成，是城市的重要组成部分。小区内的一些便利店(如包子店)通常都只服务于所在小区，较符合本文模型中不考虑区域外需求的假设，可以寻找地理形状近似为矩形的小区来描述本文模型的应用。

以安徽省合肥市梦园小区为例来进行说明。安徽省合肥市梦园小区位于合肥市高新区，小区的东、南、西、北各边分别由天柱路、梦园路、香樟大道以及海关路所围成，长度分别为550、480、560、470 m，粗略计算之下，邻边道路相互垂直且各条道路均为直线，因此可视为一个矩形区域。小区内仅有A、B 2家包子店，将小区的地理位置抽象为一个矩形，并作出如图3所示的坐标系。

图3 2家包子店的初始位置 A′、B′与均衡位置A″、B″

由于2家店主一开始都各自选择其居住地作为其店址，这样就产生了A与B的初始位置A′、B′。

使用本文模型的解决办法，2家店面都进行了重新选址。由于包子店重新选址的成本可以忽略不计，因此符合本文的假设。重新选址后2家店面的位置分别位于A″与B″。其中，A″位于小区的北门旁，位置距离小区的东北角为180 m;B″位于小区南门往里20m处。鉴于实际问题的复杂性以及各种粗略的近似，A″与B″可视为符合模型的均衡位置。

由该案例可以看出，本文模型在实际中有着广泛的应用，尤其是考虑到面向小区服务的各种便利店。由于实际问题的复杂性，实际的商店位置可能会与理论上的均衡位置存在细微的差异，但这并不影响本文模型在实际中的应用。

5 结束语

本文研究了在二维矩形市场中，消费者需要考虑空间距离成本的情况下，销售同质商品的2个寡头销售商在Bertrand-Stackelberg博弈下对商品的定价与选址问题，并提供一个实例来说明其应用。通过与 Bertrand-Nash均衡利润的比较，得出如下结论:

(1)在均衡位置方面，2个销售商仍然遵循着“最大-最小”原则。

(2)Bertrand-Stackelberg博弈更能使销售商获益，尤其是对扮演追随者角色的销售商而言更是如此，这提供了一定的管理启示。

进一步研究的问题是:对于2个销售商来说，追随者将比领先者更具有获利能力，那么，究竟由谁来扮演领先者的角色。此外，本文沿用文献[11]的假设，将2个销售商初始位置设为对称，然而，现实中销售商的位置可能是任意的。因此，进一步研究可以放宽该假设条件，将其扩展为初始位置任意的情况。另外，本文研究限于二维市场中的矩形市场，可以将矩形市场扩展为其它形状的市场来进行研究，甚至可以扩展为不规则形状的二维市场。

[1] H otelling H.Stability in competition[J].Jou rnal of Economics，1929，39:41-57.

[2] D′Asp remont C，Gabszew ics J，Thisse JF.On H otelling＇s stability in competition[J].Econometrica，1979，17: 1145-1151.

[3] Econom ides N.The p rinciple ofm inimum differentiation revisited[J].Eu ropean Economic Review，1984，24: 345-368.

[4] Gabszew ics J J，Thisse JF.Spatialcom petition and the location of firm s[M].Location theory，1986:28-47.

[5] Choi SC，Desarbo W S，Harker P T.Produ ct positioning under price competition[J].Management Science，1990，36: 175-199.

[6] Tyagi R K.Sequen tial product positioning under differential costs[J].Management Science，2000，46:928-940.

[7] Granot D，Granot F，Raviv T.On competitive sequential location in a network with a decreasing demand intensity[J]. Eu ropean Journal of Operational Research，2010，205: 301-312.

[8] 赵德余，顾海英，刘 晨.双寡头垄断市场的价格竞争与产品差异化策略:一个博弈论模型及其扩展[J].管理科学学报，2006，9(5):1-7.

[9] 刁新军，杨德礼，胡润波.具有Stackelberg博弈和网络外部性的扩展 Hotelling模型[J].系统工程，2008，26(2): 31-34.

[10] Tabuchi T.Tw o-stage tw o-dim ensional spatial competition between two firms[J].Regional Science and Urban Econom ics，1994，24:207-227.

[11] Veendorp E C H，Majeed A.Differentiation in a tw o-dimensional market[J].Regional Science and U rban Econom ics，1995，25:75-83.

[12] Chaplin A S，Nalebuff B J.M ulti-dim ensional product differentiation and price competition[J].Oxford Econom ic Papers，New Series，Supplement:Strategic Behaviour and Industrial Competition，1986，38:139-145.

[13] Larralde H，StehléJ，Jensen P.Analytical solution of a m ulti-dimensional H otelling model with quadratic transportation costs[J].Regional Science and U rban Economics，2009，39:343-349.