基于网络平台市场的销售商促销竞争策略研究

姜 璇 贾 朕 吴伶俐

(1.中南财经政法大学 工商管理学院, 湖北 武汉 430073; 2.华中师范大学 经济与工商管理学院, 湖北 武汉 430079)

0 引言

随着电子商务的迅猛发展,网络平台市场(Online Marketplace)已成为越来越多的网络零售商选择的在线运营模式,在这种模式下,销售商在网络零售商提供的在线平台上直接和顾客交易,网络零售商(后文称电商平台或平台商)按一定比率向销售商在平台上达成的每笔交易收取佣金[1-2],例如,阿里巴巴集团旗下的天猫和淘宝以及eBay网是典型的网络平台市场模式,而亚马逊和京东近年来除了维持原有的自营业务外,也在逐步扩大网络平台市场业务[3]。

在网络平台市场中,平台商经常发起平台促销活动邀请电商平台上的销售商参加,例如,天猫的双十一和双十二购物狂欢节,京东的“6.18”周年庆,亚马逊的“Prime Day”,除此之外,还有各大电商平台围绕各类节假日发起的主题促销活动如“女神节”“年货节”等。有趣的是,不同行业内竞争的销售商面对平台商发起的促销活动往往表现出了不同的态度,例如,在2019年天猫发起的跨年夜平台促销活动中,快时尚服装品牌H&M和ZARA旗舰店都没有参加平台促销活动;个人电脑品牌联想和戴尔旗舰店都参加了平台促销活动;数码相机品牌中的索尼旗舰店参加了平台促销活动,而佳能旗舰店却没有。结合这一现象,本文试图回答当销售商面对竞争时,是否应该加入平台促销活动,该如何制定店铺最优促销折扣?哪些因素将影响销售商和平台商的促销决策?平台商为什么乐于发起平台促销活动?

本研究连结了网络零售平台市场和促销两方面的文献,探讨了在竞争环境下基于网络平台市场的两个销售商,面对平台商发起促销活动时的促销选择和促销折扣决策。现有的关于网络平台市场的研究文献,多集中在比较分析网络平台市场模式(marketplace/platform scheme/agency selling)和转售模式(reseller/wholesale scheme /reselling)。一些学者在电子书籍领域比较分析了这两种模式对供应链上各成员的利润影响,例如,Hao 和 Fan[4]聚焦于出版商和电商平台对电子书籍和电子阅读器在不同运营模式下的定价问题;Lu等[5]探讨了由作者、出版商、在线书店和传统书店四者组成的供应链在不同运营模式下各主体利润的变化;Tan等[6]关注由一个出版商和两个竞争的电商平台组成的数字商品供应链在不同运营模式下的供应链协调问题。除此之外,Abhishek等[7]考虑了线上渠道的销售对线下渠道的影响和电商平台之间的竞争,研究电商平台对转售和网络平台市场的选择。Hagiu和Wright[1]发现对两种不同运营模式的选择取决于品牌商和电商平台的营销努力水平。Kwark等[2]考虑了两个竞争的品牌商和一个电商平台组成的供应链,探讨了顾客在线评论信息对制造商竞争的影响以及对电商平台运营模式选择的影响。还有些学者研究了在电商平台已经存在转售模式的情形下是否要引入网络平台市场,例如,Ryan等[8]在引入网络平台市场模式的成本和新增市场两个因素间进行权衡分析;Yan等[3]进一步考虑了线上销售对线下销量的影响以及网络平台市场模式下制造商直销渠道相比于转售渠道的低效性;Mantin等[9]发现引入网络平台市场模式将有利于提升电商平台和上游品牌商谈判时的讨价还价能力。李佩和魏航[10]比较分析了零售商经营模式的选择包括分销、平台和二者混合模式。上述文献都是从网络零售商的角度出发分析平台运营模式战略以及相关影响因素,目前基于网络平台市场的研究鲜有涉及平台商和销售商之间的促销问题。

与本文有关的另一类研究是折扣促销的相关文献。Gerstner和Hess[11]指出折扣可以分为由制造商直接向顾客提供的折扣即制造商折扣(manufacturer rebates),由制造商向零售商提供的折扣即渠道折扣(trade deals),以及由零售商向顾客提供的折扣即零售商折扣(retailer rebates)。Chen等[12]、Yang等[13]以及Martín-Herrán和Sigué[14]研究了制造商直接向顾客发布折扣对供应链的影响;Arcelus等[15]、Aydin和Porteus[16]以及Demirag等[17]比较了制造商折扣和渠道折扣对制造商利润、零售商定价和订货量的影响;Cho等[18]、Demirag等[19]和Ha等[20]考虑了供应链上的竞争因素,研究当制造商和零售商都有提供促销折扣的选择时,供应链的均衡结果。还有些学者研究了制造商和零售商间的联合促销问题,其中慕银平等[21]、王道平等[22]以及魏莹和熊礼洋[23]考虑制造商分担零售商促销成本的情形下,探讨供应链上的竞争与协调问题;Geng和Mallik[24]以及Saha和Goyal[25]从制造商和零售商共同向顾客发起促销折扣的角度出发研究了供应链协调问题,其中前者研究了由一个制造商和一个零售商组成的供应链结构上,当制造商和零售商均可直接向顾客提供邮寄折扣时,面对市场需求的不确定性,制造商和零售商的促销选择均衡策略,后者比较了在由零售商和制造商组成的二阶供应链上分别实行联合折扣合同、批发价格折扣合同和成本分担合同对供应链协调的影响。上述文献绝大部分是基于传统的供应链系统中制造商和零售商之间的转售模式探讨促销问题,而网络零售平台市场的运营模式和转售模式有本质区别,前者网络零售平台和销售商的关系建立在佣金费率合同之上,而后者制造商和零售商关系大都建立在批发价格合同之上,该差异使得网络零售平台市场上的促销问题区别于上述文献,基于此本文围绕网络零售平台市场上销售商的促销竞争问题展开了研究。

在查阅的所有文献中同时聚焦网络零售平台市场模式与促销问题的文献非常少,与本文研究内容较为相近的文献是王聪和杨德礼[26]、姜璇等[27]以及Li和Deng[28]。王聪和杨德礼[26]探讨了由制造商和传统零售商以及网络零售平台商组成的供应链,当平台商发放折扣券时对供应链上各成员定价决策和利润的影响,该研究讨论的场景是仅平台商提供折扣,且研究的对象是制造商传统线下渠道和线上直销渠道的双渠道问题,而本文关注的是由一个网络零售平台商和入驻其上的多个销售商组成的渠道结构,平台商提供促销活动,销售商们可以选择是否加入,探讨销售商们的促销选择博弈,以及销售商和平台商的折扣决策。姜璇等[27]比较分析了网络零售平台和销售商之间三种不同的促销情景下(包括由平台商率先发起促销邀请销售商参加,由销售商发起促销邀请平台商参加以及二者独立发起促销),平台商和销售商何时应该进行单边促销,何时应该进行双边促销;Li和Deng[28]研究了网络零售平台市场上一个销售商和平台商同时向顾客发起促销时的均衡策略。上述两篇论文虽然围绕网络零售平台上的折扣促销活动展开了研究,但是均未考虑平台上存在多个销售商时的竞争因素。

本文和上述三篇论文的主要区别在于本文围绕一个网络零售平台商和竞争的销售商构建了一个三阶段的促销博弈模型,研究销售商们面对平台商发起促销活动时的促销选择均衡策略以及销售商和平台商的最优促销折扣决策,并详细分析了竞争程度和佣金费率对销售商和平台商促销决策以及利润的影响。本文的贡献主要体现在以下几个方面:(1)研究的对象是网络零售平台上平台商和销售商的联合促销问题,平台商和销售商之间施行佣金费率合同,销售商面对平台商发起的联合促销活动可以有参加或者不参加多项选择;(2)考虑多个销售商之间的竞争因素,探讨销售商们和平台商的促销竞争均衡策略,包括销售商是否应该参加联合促销,以及销售商们和平台商该如何制定最优折扣决策;(3)研究发现销售商们都不参加、或部分参加或者全部参加平台促销活动均有可能成为均衡策略,结果受到销售商们参与成本和平台商制定的佣金费率等因素的影响,且随着竞争的加剧,销售商的利润并非一定受到伤害,平台商的利润也并非一定获益。

1 基本问题描述和模型构建

促销季,在网络平台市场上平台商发起平台促销活动,邀请平台上的销售商参加,销售商可以选择参加或者不参加平台促销活动。选择参加的销售商需要承担加入平台促销的营销费用(https://www.iyiou.com/p/85349.html)和活动订单处理费用等成本,顾客在购买该销售商的商品时,不仅可以享受店铺折扣,同时可以享受平台商给顾客提供的平台折扣;选择不参加的销售商,仍然可以提供店铺折扣来促销商品,但是购买其商品的顾客无法享受平台提供的折扣。平台商将根据销售商的参与情况,制定具体的平台促销折扣,销售商根据平台商具体的折扣策略和对手是否参加平台促销活动的选择策略,分别制定自身店铺折扣策略。

本文假设平台商和销售商提供的折扣均为即时扣减型,不存在顾客的兑换过程,类似于网上流行的电子折扣券/代金券等形式,同时另假设在促销过程中,商品的日常价格保持不变,这符合近年来国家工商总局和相关电商平台对销售商参与促销活动的规定,以防止出现虚假促销(http://news.cctv.com/2017/11/02/ARTIkobzVzGmFXMxtPcOgipn171102.shtml)。

本文模型中考虑两个销售商S1和S2在网络平台市场上销售具有替代性的商品,若二者均选择加入平台促销活动,根据二者运作和营销能力的不同,将分别产生Fi(i=1,2,下同)的固定费用,包括加入平台促销的营销费和运营费等。平台商对销售商在网络平台市场达成的每笔交易按比率λ收取佣金,为了简化分析,假设二者销售的商品进货成本均为c。平台商发起网络平台市场促销活动后,销售商和平台商的决策过程如下:

第1阶段:销售商面对平台商发起的网络平台市场促销活动,决定是否参与,令Zi=R,表示销售商Si决定参与平台促销活动,此时将产生费用Fi,Zi=N,表示销售商Si拒绝参与平台促销活动;

第2阶段:平台商根据销售商的参与情况,决定自身提供的平台促销折扣,该折扣在参与平台促销活动的销售商之间通用,若无销售商参与平台促销活动时,平台商将不会提供平台折扣;

第3阶段:销售商Si在获取平台商的具体促销折扣信息后,同时决定各自的店铺促销折扣

2 三种情形下的促销折扣决策

当销售商们面对平台商发起的网络平台市场促销时,二者选择是否要参与平台促销活动,最终会呈现出三种可能的结果,包括:二者都不参加平台促销活动,其中之一参加,以及都参加。本部分给定销售商的促销选择策略,分别求解和分析这三种情形下销售商和平台商的最优促销折扣决策,为第四部分最终求解两个竞争的销售商促销选择博弈问题做准备。

2.1 两个销售商都不参与平台促销的情形

在这种情形下,两个销售商都不参与平台促销活动,即(Z1,Z2)=(N,N)。此时,平台商不会提供平台促销折扣,但销售商仍需要决定各自的店铺促销折扣

本文中对两个竞争的销售商各自需求函数的构建参考了以往运营与营销领域的相关文献[29-32],在这种情形下,销售商分别销售的两种商品的需求函数表示为:

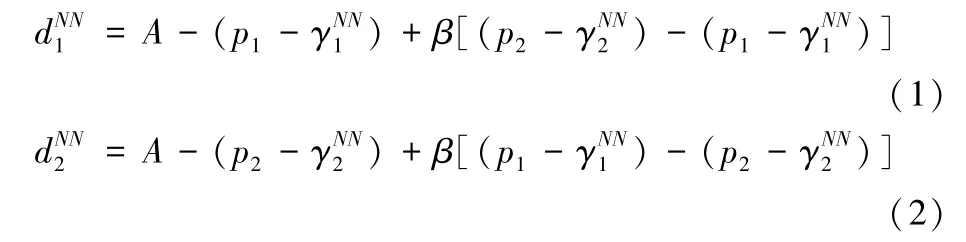
其中,A为网络平台的潜在市场规模,β表示销售商之间的竞争程度,pi为销售商Si日常的销售价格。参考Tian等[32]和Geng等[33]对模型中参数的处理,为了使这种情形下的最优促销折扣决策存在并且可能成为均衡解,假设参数的取值范围为:

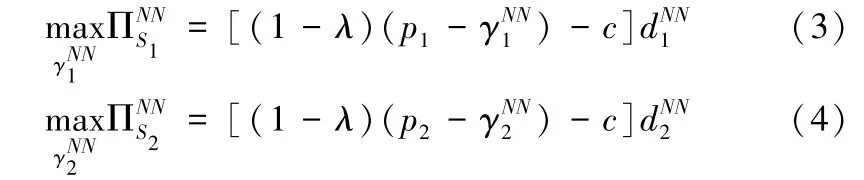
当两个销售商选择都不参与平台促销活动时,平台商无需决策平台促销折扣,由于本模型中λ为外生变量,此时平台商的利润完全取决于销售商,平台商的利润函数表示如下:

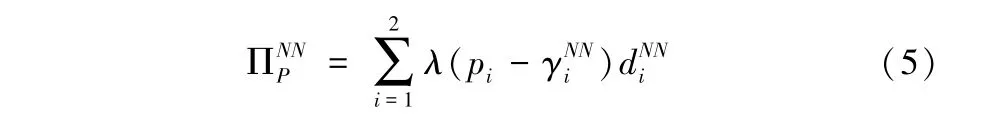
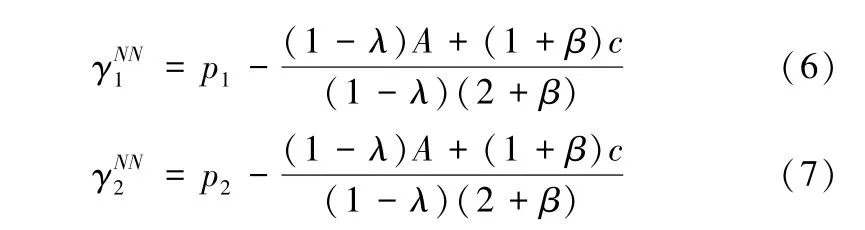
根据上述最优折扣决策,求出二者的最优利润以及平台商的利润分别如下:

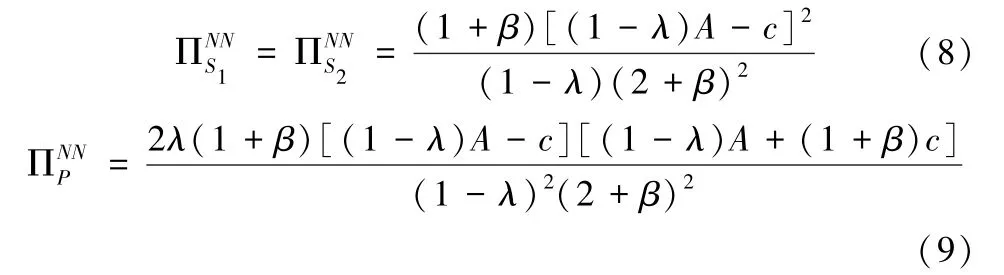
引理1是λ的非增函数,是β的非减函数;是λ、β的非增函数。

引理1 的结果符合直觉,当两个竞争的销售商在促销季选择不参加平台促销活动时,各自提供的店铺折扣力度和能获得的利润均受到二者竞争激烈程度和平台收取的佣金费率的影响,当竞争更激烈时,二者将提高促销折扣,利润也会由此减少;当平台商提高了佣金费率时,二者利润会减少,为了防止利润的进一步降低销售商将会减少促销折扣。

从引理2可以看出对于平台商来说,针对成本较低的商品,平台上销售商之间的竞争太激烈对自身并非一定有益。平台商的利润取决于销售商在平台上的交易额,每当销售商能成功交易一单位商品,则平台商便可赚取一份利润,简言之只要顾客在平台上多一份需求,平台商便可多一份获利,因此顾客需求量对平台商来说至关重要。销售商之间的竞争激烈程度影响了销售商对商品的定价,进而影响了商品的需求量,当销售商之间的竞争越激烈时,商品定价越低,顾客需求越多,销售商和顾客在平台上的成交量越多,则平台商能获得更多份的收益。但是另一方面,当商品的成本较低,使得竞争的销售商们对商品的均衡定价本身较低时,激烈的竞争将进一步降低销售商的成交价格,随着竞争程度的加剧,促销变为恶性价格竞争的手段,销售商的成交价格往往过低,此时增加的竞争程度带来的需求量的增加而产生的利润的增加少于由于单位成交价格过低导致的利润的减少,平台商的总利润也因此受损。

引理3存在λ0∈(0,1),当λ∈[0,λ0]时,为λ的非减函数,当λ∈(λ0,1]时,为λ的减函数。

证明:

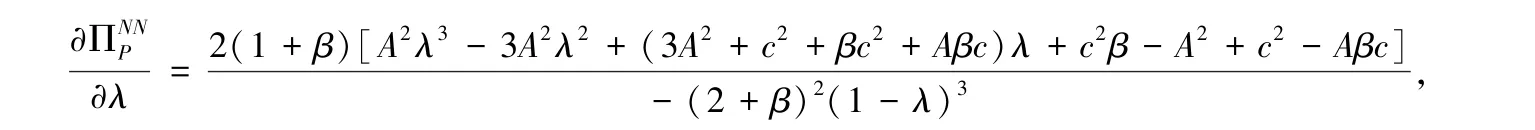
令f(λ)=A2λ3-3A2λ2+(3A2+c2+βc2+Aβc)λ+c2β-A2+c2-Aβc,f′(λ)=3A2λ2-6A2λ+3A2+c2+βc2+Aβc,Δ=36A4-12A2(3A2+c2+βc2+Aβc)=-12(c2+βc2+Aβc)＜0,又因为f(λ=0)=c2β-A2+c2-Aβc=βc(c-A)-(A2-c2)＜0,且f(λ=1)=2c2(1+β)＞0,因此根据三次函数f(λ)的性质,一定存在λ0∈(0,1),使得f(λ=λ0)=0,当λ∈[0,λ0]时,为λ的非减函数,当λ∈(λ0,1]时,为λ的减函数。 证毕。

引理3指出平台商提高佣金费率不一定对自身有利,随着佣金费率的升高,销售商会减少促销折扣,提高单位商品的成交价格,从而避免进一步损失利润,当佣金费率过高时,虽然平台商能够从销售商处获得较高的单位商品成交收益,但是会因为商品成交数量的锐减而使得总利润降低。

2.2 仅一个销售商参与平台促销的情形

在这种情形下,一个销售商选择参加平台发起的促销活动,另一个选择不参加,不失一般性,设销售商S1参加平台促销,S2不参加,即(Z1,Z2)=(R,N)(销售商S2参加平台促销,S1不参加的情形与此类似)。平台商根据销售商参与情况,首先制定平台促销折扣,两个销售商在观察到平台商的促销决策后,同时分别决定店内促销折扣(i=1,2)。同2.1情形假设类似,为了使这种情形下的最优促销折扣决策存在且可能成为均衡解,假设参数的取值范围为,其中R,N,M,G,S,H的取值见后文。

按照逆向求解思路,先对两个销售商的决策问题求解。当S1参加平台促销活动,S2不参加时,商品的需求函数分别为:

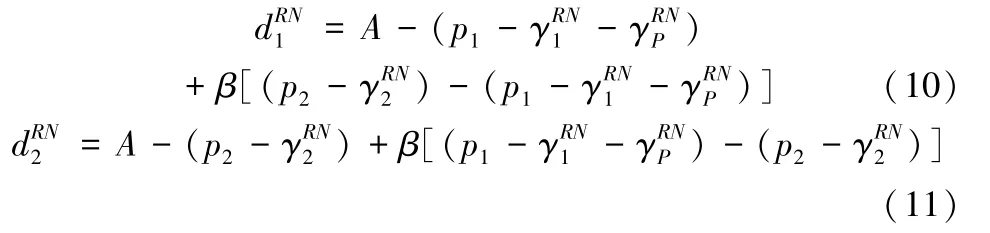
从式(10)-(11)可以看出,随着平台促销折扣的提高,销售商S1的商品需求量增加,销售商S2的商品需求量减少。销售商的利润函数分别如下所示:

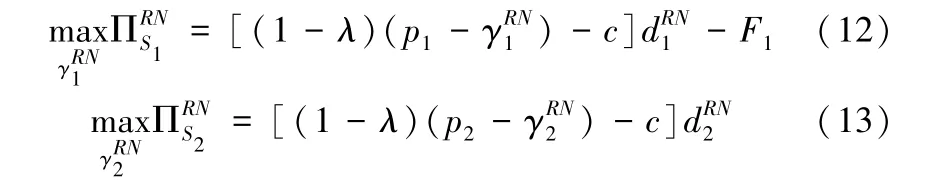
可以证明二阶Jacobian矩阵为负定,式(12)-(13)存在唯一的Nash均衡解。令联立求解,可得两个销售商关于平台商促销折扣的反应函数,分别为如下表达式:

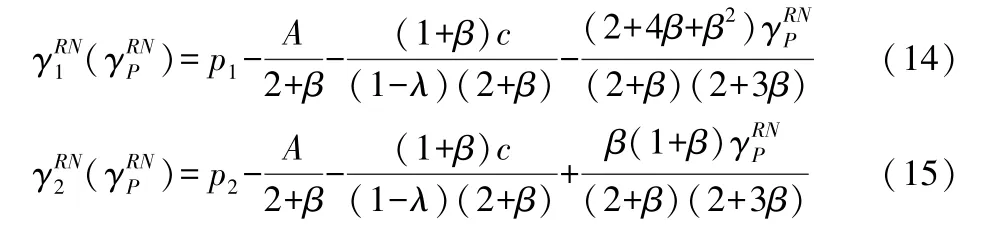
由式(14)-(15)可以看出,销售商的促销折扣直接受到平台促销折扣的影响,随着平台商提供的促销折扣升高,参加平台促销活动的销售商S1将降低自身的店铺促销折扣,而未参加平台促销的销售商S2将跟随平台商提高自己的店铺促销折扣。

接下来,求解平台商的决策问题,平台商的利润函数为:

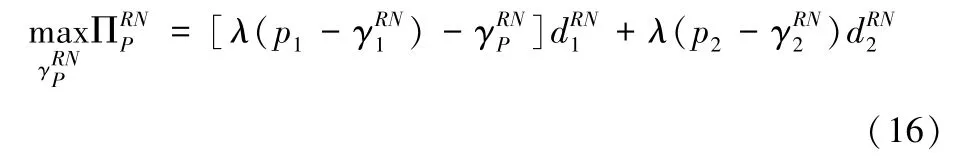
平台商在制定平台促销的决策过程中,会考虑销售商的反应,将式(14)-(15)带入式(16)中,因为,则令,可以求出平台商的最优促销折扣:

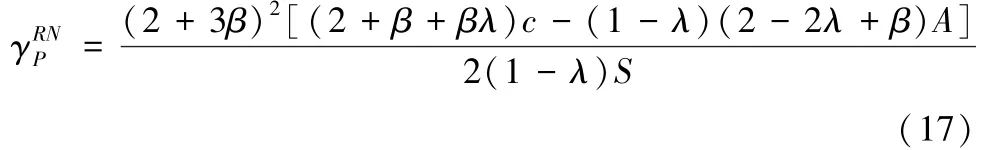
将式(17)带入式(14)-(15)中可以求得销售商的最优店铺促销折扣分别如下,其中S,M,G,N,H分别为λ和β的函数,表示如脚注所示①S=(3-2λ)β4+(20-10λ)β3+(42-21λ)β2+(32-16λ)β+8-4λ;M=(1-λ)[(3-4λ)β3+(14-6λ)β2+(14-2λ)β+4];N=(1-λ)[(9-4λ)β3+(33-18λ)β2+(30-16λ)β+8-4λ];H=(1+β)[(6-4λ)β3+(25-15λ)β2+(26-14λ)β+8-4λ];G=(6-4λ)β4+(37-13λ)β3+(70-22λ)β2+(50-16λ)β+12-4λ.:

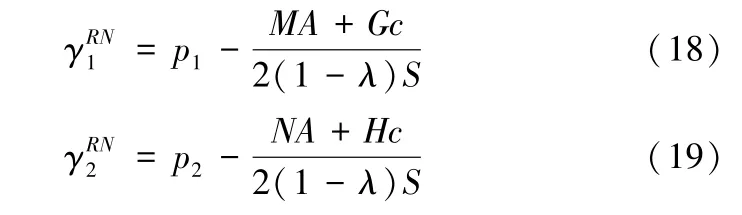
由式(17)-(19)可以求解出销售商和平台商的利润分别为, 其中R和Q分别为λ和β的函数,表示如脚注所示②R=(9-λ)β3+(33-13)β2+(30-14λ)β+8-4λ;Q=(3-7λ)β3+(14-20)β2+(14-16λ)β+4-4λ.:

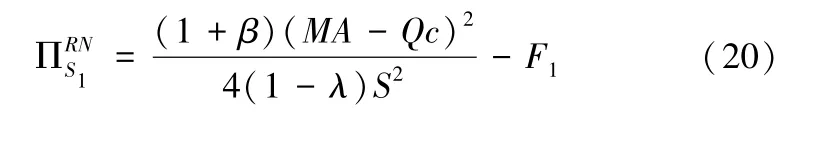
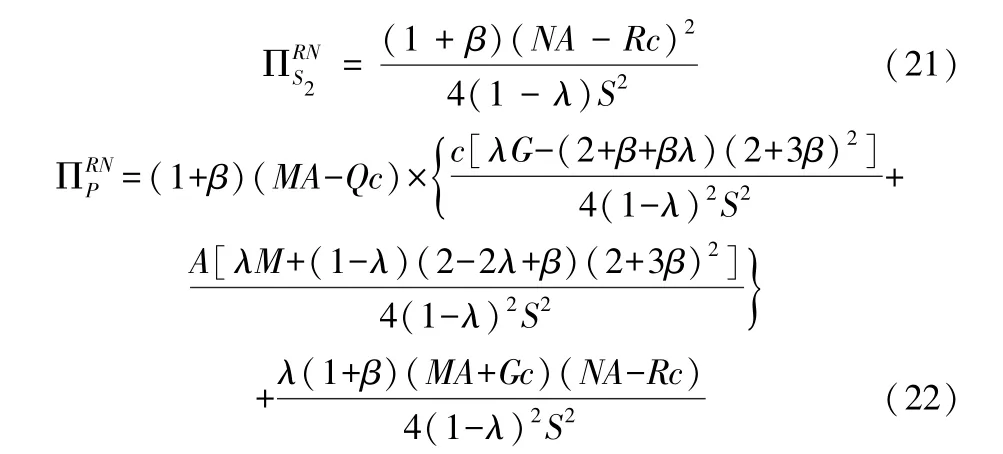
引理4为λ的增函数,(i=1,2)为λ的减函数①由于证明过程较为繁琐,受到版面限制不能在正文中呈现,详细的分析过程可以向作者发邮件索取:jiangxuan@zuel.edu.cn。

引理4中关于销售商促销折扣和佣金费率的变化关系类似于引理1中的分析结果。从引理4中还可以看出,当平台商向销售商收取的佣金费率升高时,平台商对销售商单笔销售提成升高,将会进一步提高平台的促销折扣,以刺激平台上的交易量,从而提升总的收益。

相比较于(N,N)情形中平台商只能被动接受从销售商处获得的佣金收益,在(R,N)情形下,平台商可以通过调节平台促销折扣来调节销售商在平台上最终达成交易的价格,使得在该成交价格下自己的利润最大化。从图1可以看出,随着竞争越激烈,销售商均会提高促销折扣,利润会降低,这和引理1的分析相一致,而相应地平台商会降低平台促销折扣,这是因为随着销售商促销折扣的升高,使得销售商的最终成交价格降低,平台商通过减少平台促销折扣可以使得销售商最终的成交价格和成交量保持在最大化自身利润的水平上,与此同时,随着平台商促销折扣支出的降低,平台商的利润会升高。因此,从图1中可以看到销售商之间的竞争程度升高,将使得平台商利润的增加。

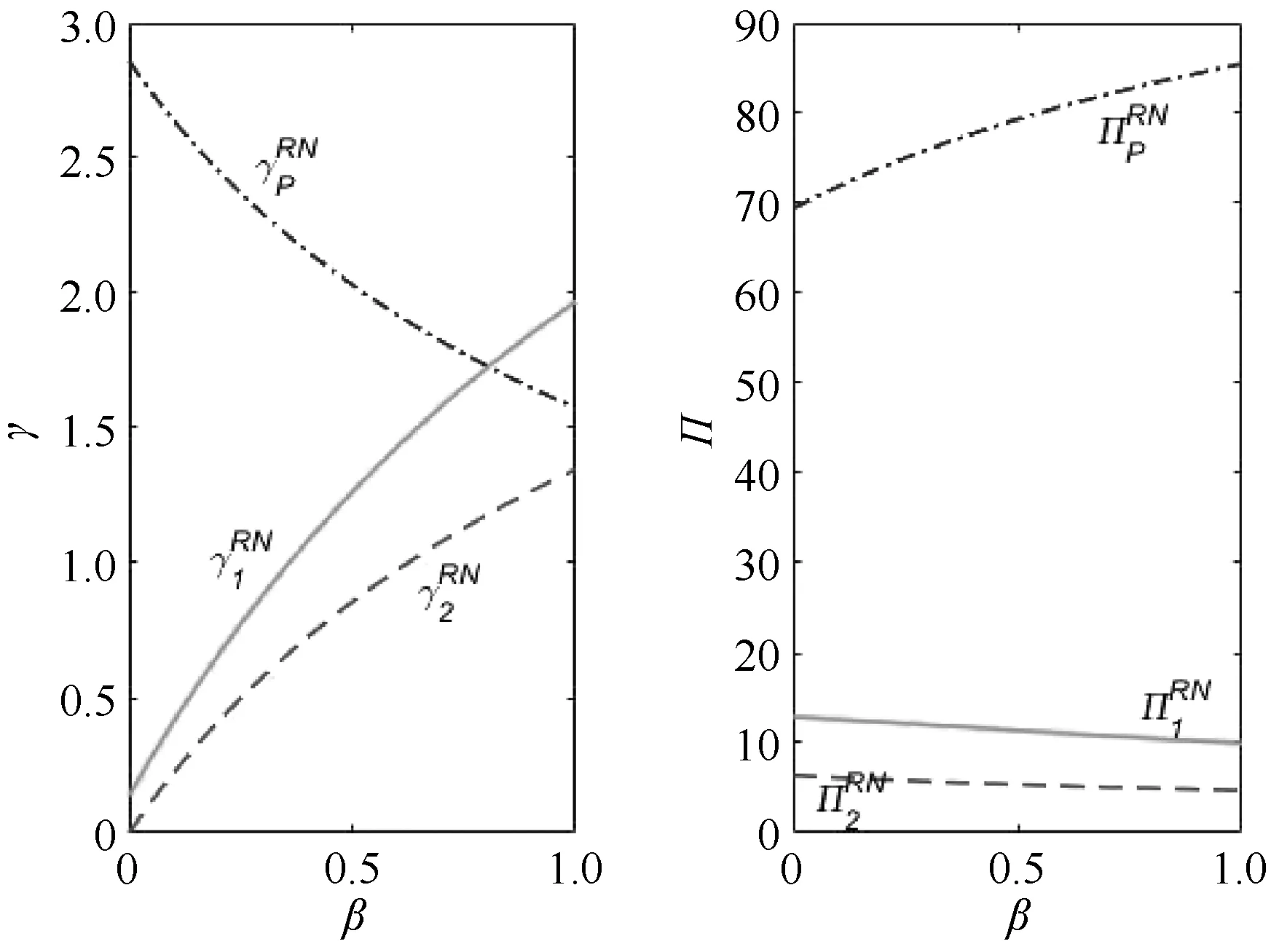
图1 (R,N)情形下促销折扣、利润与竞争的关系Figure 1Relationship of rebates, profit,and competition coefficient under (R,N)

令β=0.15,A=47,c=10,p1=45.207,p2=41.997,分别作出和(i=1,2)与λ的关系图,以及和与λ的关系图,如图2所示。图2中第一列子图显示了和(i=1,2)分别随λ变化的趋势印证了引理4。第二列子图展示了在(R,N)情形下销售商的利润随佣金费率的升高而降低,与引理1分析结果一致。平台商的利润随佣金费率的升高先增加后减少,和引理3结论一致,除了引理3背后的原因,还因为随着佣金费率的升高,虽然平台商能够从销售商每笔交易额中获得较高的提成,但是平台商的促销折扣随之升高,由于销售商S1和S2的竞争关系,S2未参加平台促销活动,这间接导致顾客从销售商S2处购买的需求量降低,当佣金费率高于某一阈值时从而使得平台商从销售商S2处获得收益的降低带来的损失超过了平台商从销售商处获得的单位交易额提成的升高带来的利益,从而使得平台商总利润降低。

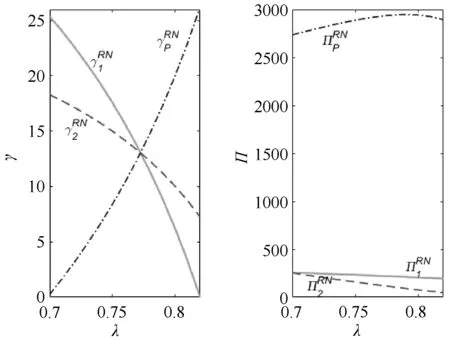
图2 (R,N)情形下促销折扣、利润与佣金费率的关系Figure 2Relationship of rebates, profit, and commission rate under (R,N)

2.3 两个销售商均参与平台促销的情形

在这种情形下,销售商S1和S2均参与平台促销活动,即(Z1,Z2)=(R,R)。平台商根据销售商参与情况,首先制定平台促销折扣γPRR,两个销售商在观察到平台商的促销决策后,同时分别决定店内促销折扣γiRR(i=1,2)。同2.1和2.2情形假设类似,为了使这种情形下的最优促销折扣决策存在且可能成为均衡解,假设参数的取值范围为:c≤A≤

按照逆向求解思路,先对两个销售商的决策问题求解。当S1和S2均参加平台促销活动时,商品的需求函数表示如下:

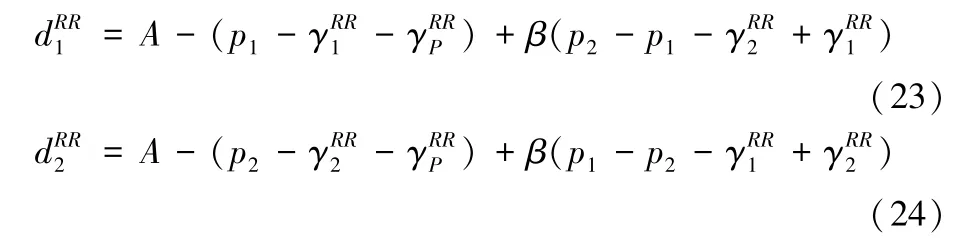
从式(23)-(24)可以看出,随着平台促销折扣的升高,销售商的商品需求均会增加。销售商S1和S2的利润函数分别为:

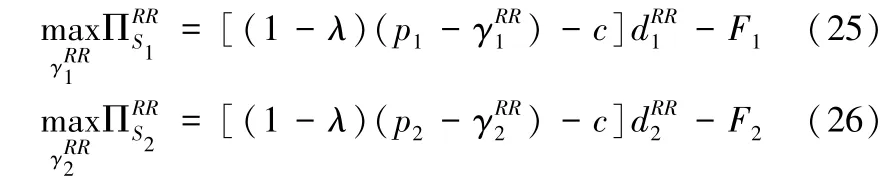
可以证明二阶Jacobian矩阵为负定,式(25)-(26)存在唯一的Nash均衡解。令联立求解,可得销售商Si(i=1,2)关于平台商促销折扣的反应函数如下所示:

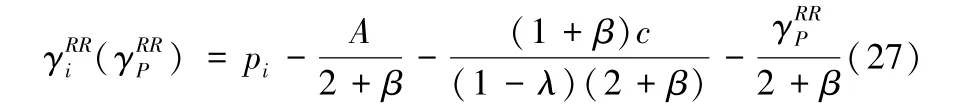
由式(27)可以看出,销售商的促销折扣直接受到平台促销折扣的影响,当销售商均参加平台促销活动时,随着平台商提供的促销折扣升高,销售商均会降低自身的店铺促销折扣。

接下来,求解平台商的决策问题,平台商的利润函数为:

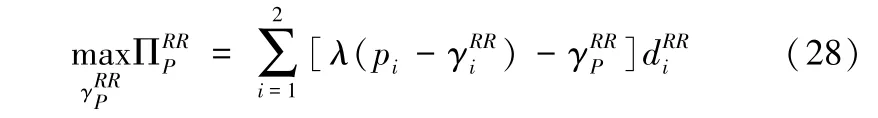
平台商在制定平台促销的决策过程中,会考虑销售商的反应,将式(27)带入式(28)中,因为0,可以求出平台商的最优促销折扣:

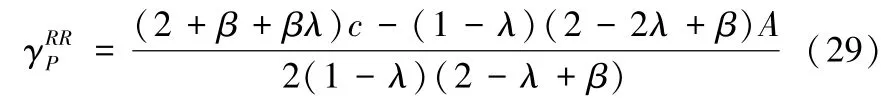
将式(29)带入式(27)中,得到销售商Si(i=1,2)的最优店铺促销折扣决策为:

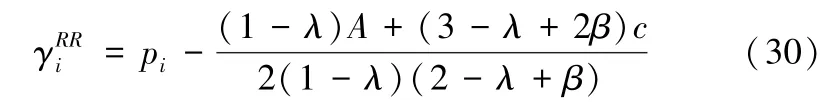
由式(29)-(30)可以求出销售商和平台商的利润分别为:

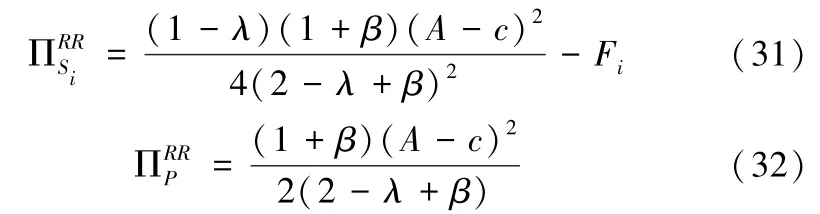
引理5是λ的增函数,是β的非增函数;(i=1,2)是λ的减函数,是β的非减函数。

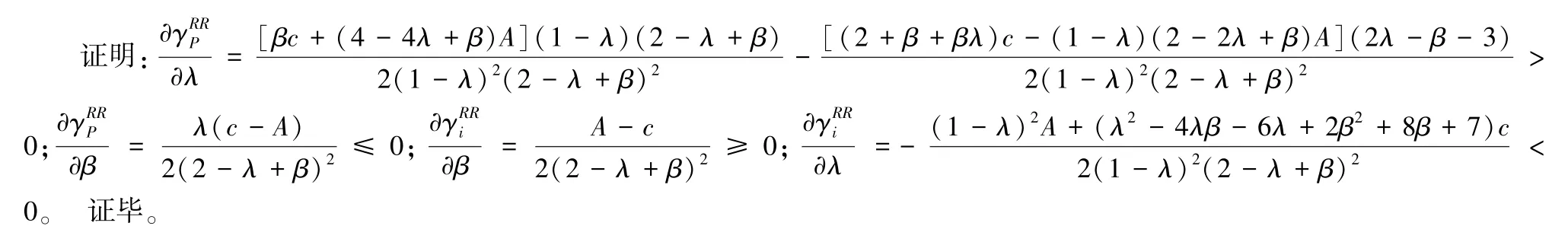
引理5中关于销售商、平台商的促销决策和佣金费率的变化关系,类似于引理4中的分析结果,销售商、平台商的促销决策和竞争程度的变化关系,与2.2中数值分析结果相一致。

引理6(i=1,2)是λ、β的非增函数;是β的非减函数,是λ的增函数。

引理6中关于(R,R)情形下,销售商的利润和佣金费率、竞争程度的变化关系,以及平台商的利润和竞争程度的变化关系类似于2.2中数值分析结果,然而,在这种情形下平台商的利润随佣金费率的变化关系和引理3以及2.2中相关数值分析结果并不一致,平台商的利润随着佣金费率的升高而单调递增。这是因为当所有销售商都参加平台促销活动时,若平台商提高佣金费率,虽然销售商会减小店铺促销折扣,但平台商会相应提高平台促销折扣,且平台促销折扣升高的幅度大于销售商店铺折扣降低的幅度从而使得销售商的商品需求增加,与此同时,由于销售商店铺促销折扣的降低,平台商从销售商处获得的每单位交易提成升高,因此,随着佣金费率的升高,平台商的总利润升高。

3 销售商促销选择博弈分析

3.1 三种情形的横向比较

第2部分求解分析了每种情形下平台商和销售商的最优促销折扣决策以及相关参数对决策的影响。为了使得三种情形均有可能成为销售商促销博弈过程中的均衡解,因此假设参数满足以下条件:

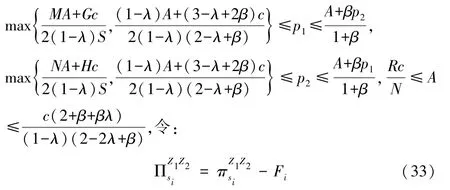
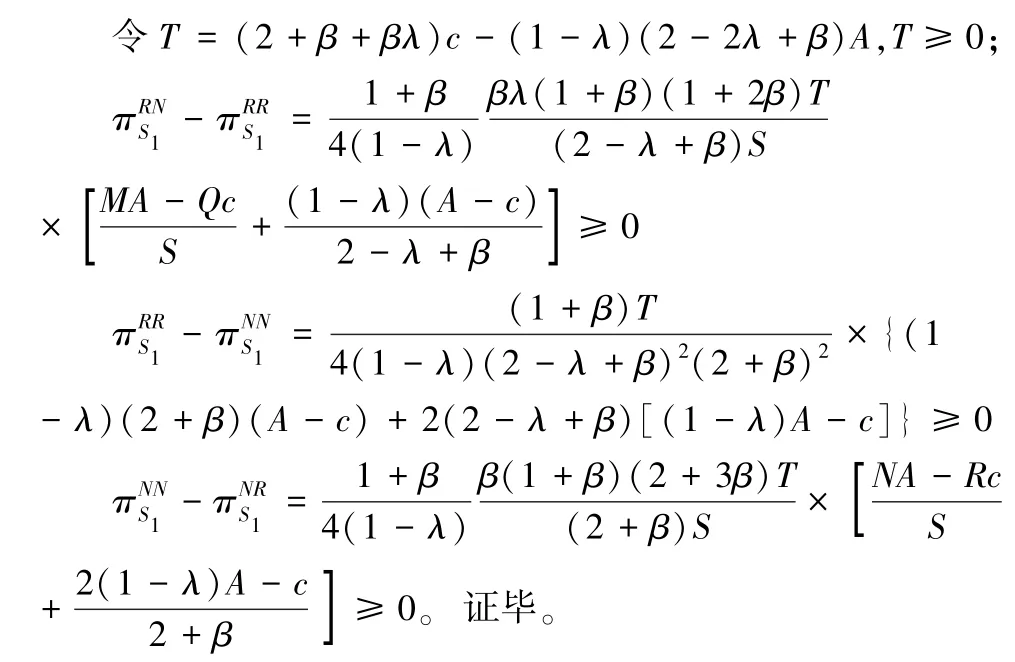
从命题1可以看出,销售商选择都不参加平台促销活动时所制定的最优店铺折扣要高于二者均参加平台促销情形下所提供的店铺促销折扣,若仅有一方销售商参加平台促销,参加的一方制定的店铺折扣值最小,未参加的销售商制定的店铺折扣值最大。对销售商来说,若不考虑参加平台促销活动的成本,其在仅自身参与平台商促销活动的情形下获得的收益最高,双方同时参加平台商促销情形下其获得的收益次之,双方均不参加平台商促销的收益小于前面两种情形,在竞争对手参与平台促销而自身不参加的情形下收益最低。命题1说明了销售商参与平台促销活动在一定程度上有利于缓解竞争,在不考虑参加平台促销活动的成本时,销售商参加平台促销活动会有助于收益的提升。

命题2在有销售商参与平台促销活动的情形下,平台商提供的平台促销折扣大小关系为:;在三种情形下平台商的利润大小关系为:。

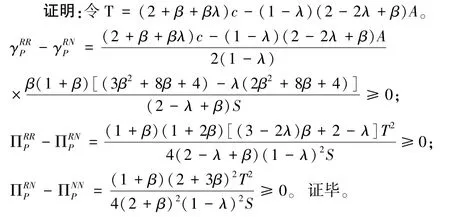
从命题2可以看出对于平台商来说,当两个销售商同时参加平台促销活动时,其制定的平台促销折扣最大,获得的利润也最高。这是因为当仅有一个销售商参与平台促销活动时,考虑到未参加的销售商,由于竞争的存在,平台商不能够把平台促销折扣制定得很高,未参加的销售商制定的店铺折扣随着平台促销折扣的升高而升高,较高的店铺折扣使得平台商从这部分销售商中抽取的单位商品佣金收入降低;而当所有销售商均参加平台促销时,平台商的折扣会制定得更高,因为较高的平台折扣会使得销售商的店铺折扣更低,但是总的需求量会更高,这会更有利于提高平台商的利润。

命题2 还指出当销售商均不参加平台促销时,平台商的利润最低。这是因为,当销售商参加平台促销时,平台商可以通过调整平台促销折扣来影响销售商的店铺促销折扣的制定,从而间接控制销售商最终的成交价格,因此,相较于无销售商参与平台促销活动时平台商只能被动获取利润的情形,平台商在有销售商参与平台促销活动的情形下,利润更高。命题2解释了现实生活中各大电商平台频繁制造促销节日,争夺不同品牌的销售商参与平台促销活动背后的动机。

3.2 最终博弈结果分析

在第1阶段的决策中,销售商面临是否选择加入平台商发起的平台促销活动的决策。若销售商加入平台促销活动会产生固定费用Fi(i=1,2),下表1展现了两个竞争的销售商在三种情形下的利润矩阵:

表1 销售商在促销选择博弈中的利润矩阵Table 1Profit matrix for the sellers in the promotion selection

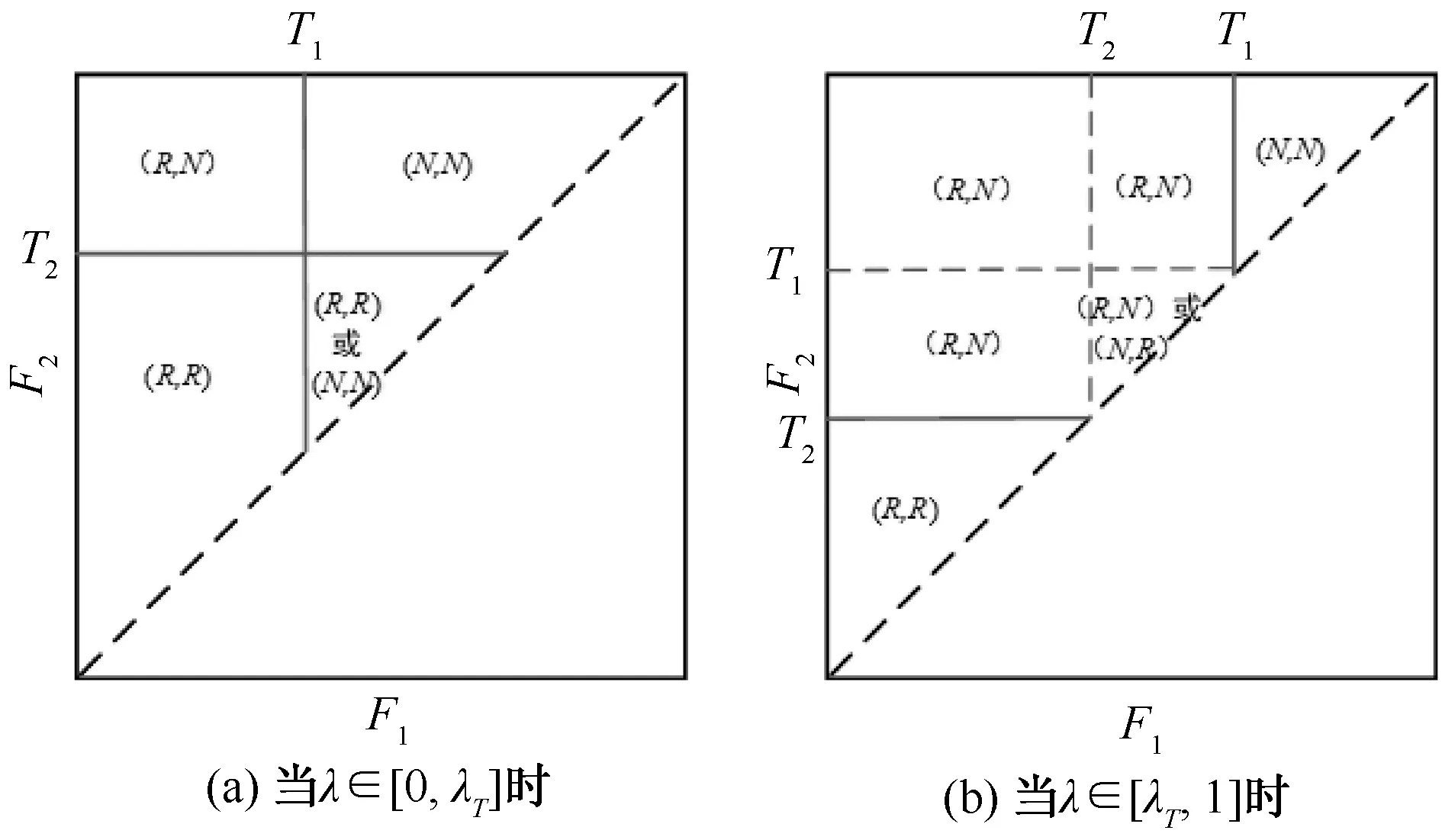
图3 销售商促销选择博弈均衡策略区域图Figure 3Regional map of the sellers′ equilibrium promotion strategy

命题3(1)当λ∈[0,λT]时:①若F1＜T1且F2＜T2,(R,R)是唯一的均衡解;②若F1＞T1且F2＞T2,(N,N)是唯一的均衡解;③若F1＜T1且F2＞T2,(R,N)是唯一的均衡解;④若T1＜F1＜F2＜T2,存在两个均衡解(R,R)和(N,N),其中(N,N)为帕累托最优策略。(2)当λ∈(λT,1]时,即T1＞T2:①若F1≤F2＜T2,(R,R)是唯一的均衡解;②若T1＜F1≤F2,(N,N)是唯一的均衡解;③若F1＜T1且F2＞T2,存在(R,N)是唯一的均衡解或者存在两个均衡解(R,N)和(N,R)。

命题3指出当佣金费率较小时,若两个销售商参与平台促销活动的成本都较小,则都应该选择参加平台促销活动;若促销成本均较大,则都不应该参加平台促销活动;若一个销售商促销成本较小,另一个较大,则成本较小者应该参加,较大者不应该参加;若两个销售商的成本都处于中等水平,二者同时参加或者同时不参加均可能成为博弈均衡结果,其中二者同时不参加将会是帕累托最优策略。当佣金费率较高时,从图3(b)可以看出促销成本较低的一方参加平台促销活动,而促销成本较高的另一方选择不参加将更可能成为系统博弈均衡结果。

从命题3还可以推导出当T3＜Fi＜Ti(i=1,2)时,(R,R)策略是唯一均衡解,但是两个销售商在(N,N)策略下利润更高,这就是经典的囚徒困境问题。当一方销售商选择参加平台促销活动时,另一方销售商也会选择参加,否则他会获得最低利润。

基于命题3分析销售商和平台商的利润随着竞争程度变化的趋势如图4所示,图中参数取值分别为:A=22.051,p1=19.852,p2=19.853,λ=0.362,c=10,F1=1.55,F2=2.05。

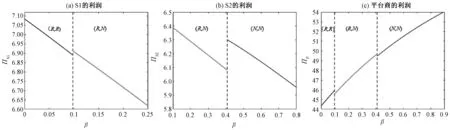
图4 销售商和平台商的利润随竞争程度变化趋势图Figure 4Relationship of the profit for the sellers and the platform, and the competition coefficient

从图4中的子图(a)和(b)可以发现一个有趣的现象,销售商之间竞争程度的增加并非一定会伤害销售商的利润。在销售商均参加平台促销的情形下,随着竞争趋于激烈,当其中一方,例如销售商S2,因为竞争获得的收入持续减少直到其扣除参与平台促销活动的成本得到的净利润低于不参加时能获得的利润,这时S2会选择不参加平台促销,而另一方,例如销售商S1,在竞争对手退出平台促销时,即促销选择博弈均衡策略由(R,R)变为(R,N)时,自身利润会有阶跃式地提升;类似地,当销售商之间的竞争程度持续增加时,S1也会因为参与平台促销活动产生的费用高于得到的收益而退出活动,此时对之前未参加活动的销售商S2来说,促销选择博弈均衡策略由(R,N)变为(N,N)时,S2的利润会有阶跃式地提升。

从图4中的子图(c)可以发现,对平台商来说,当有销售商参加平台促销活动时,随着销售商竞争激烈程度的增加,对自身的利润并非一定有益,这是因为销售商之间的竞争越激烈,销售商的利润在某一均衡策略中会持续下降,最终当销售商参加平台促销活动所能获得的收益要低于成本支出时,销售商将不会选择参加平台促销活动。因此,竞争越趋激烈,参加平台促销活动的销售商数量将逐步减少,随着销售商促销选择博弈均衡策略改变,平台商的利润将呈现阶跃式地下降。

本文的主体模型主要研究了两个销售商在网络零售平台上的促销竞争策略,当销售商的数量大于两个时,由于参与促销竞争博弈的各方均衡策略具有多样性和分析复杂性的特点,很难用理论模型具体推导出销售商的均衡解进行详细分析(Demirag等[19]、Boyaci和Gallego[34])。本文尝试将销售商的个数拓展为n个时通过理论分析探讨销售商的竞争均衡策略的特点,并对三个销售商参与促销竞争的特殊情形进行了数值实验分析①由于版面限制,详细的分析过程可以向作者发邮件索取:jiangxuan@zuel.edu.cn,研究结果表明命题3中的主要结论依然成立,即当销售商们的参与成本均较低时,销售商们都将参加平台促销活动,而当参与成本均较高时,销售商们都不会参加平台促销活动,销售商们都参加、都不参加或者部分参加平台促销活动的策略均有可能成为促销博弈均衡策略,其分布受到佣金费率和销售商参与成本的影响。

4 结语

在网络平台市场中,电商平台发起促销活动邀请平台上的销售商参加是常见的商业现象。面对平台商的促销活动,不同行业内存在竞争关系的销售商在决定是否参加时,往往表现出了不同的选择。本文分别研究了两个竞争的销售商在选择都不参加、仅有一个参加和都参加平台促销活动这三种情形下的销售商、平台商最优促销折扣决策问题,在此基础上,进一步通过博弈分析得出销售商促销选择的均衡策略,并探讨了销售商之间的竞争程度以及平台商收取的佣金费率的变化对均衡策略和最优折扣决策的影响。研究发现,对销售商们来说,当参加平台促销活动时自身提供的最优店铺折扣要比不参加平台促销活动时的情形低,因此参加平台促销活动在一定程度上可以缓解竞争;销售商们选择是否参加平台促销活动将受到佣金费率和参与成本的影响,特别地,当销售商们参与成本均趋近于零时,销售商们将都将选择参加平台促销活动,当销售商的成本处于中等偏低水平时,销售商们的促销选择博弈将陷入“囚徒困境”,即销售商们均会选择参加促销活动,但是若二者都不参加,彼此将会得到更高的利润。对平台商来说,平台商的利润同时直接受到两个因素的影响,包括提供平台折扣的支出和从销售商每笔交易的收入提成,当销售商参加平台促销活动的数量越多,销售商间促销竞争才能趋于平和,平台商从销售商每笔交易的提成收入才会较高,平台商也才有动力提供更高的平台促销折扣,从而激发更多的顾客需求,其获得的总利润也才能更高;另外,平台商制定较高的佣金费率也并非总是对自身有利,在有的情形下过高的佣金费率将使得平台上销售商的交易量锐减,从而给平台商带来利润损失。研究还发现,随着销售商竞争的加剧,平台商并非一定会从中获益,销售商也并非一定会利益受损,当销售商无法承担参加平台促销活动的成本而选择退出时,选择继续参加平台促销活动或者原本未参加平台促销活动的另一方销售商的利润将会升高,平台商的利润将会降低。

本研究为企业在实践过程中提供了一些有趣的管理学启示,例如,平台商应该激励平台上的销售商加入平台促销活动,这样可以为自身带来更多的利润,另外,虽然平台上销售商激烈的竞争有助于给顾客带来更多的让利,从而为平台带来更多的顾客流量并产生更多的交易,但是平台商对加剧销售商之间竞争程度的行为应该持有谨慎的态度,这是因为若销售商由于竞争过于激烈而无法承担相关成本从而退出促销活动将损害平台商的收益;销售商们在选择是否应该加入平台促销活动时,成本较低的一方应该选择加入平台促销活动,而成本较高的一方应该选择不加入,但若二者的参与成本均较低,则二者都应该加入平台促销活动,若二者的成本均为中等或者较高的情形,则二者均不参加平台促销活动才是最优的选择。

本研究中的模型在一些方面具有局限性,未来研究可以从以下两个方面进行扩展:一是本文模型针对的促销活动是商家提供即时折扣(例如电子优惠券等),顾客在消费过程中直接兑现这类折扣而不存在任何成本,而对于另一类有兑现成本的促销折扣,需要考虑顾客的兑现率,本文的模型不适合;二是本文考虑的是短期的促销活动,商品销售价格是固定的,但对于长期的促销活动,价格可能也会是销售商需要决策的变量。