渐进非负曲率流形的Poisson方程解的估计

赵成兵

(安徽建筑工业学院数学系，安徽合肥 230022)

那么Poisson方程Δu=f有一解u，即

结合引理5可知结论成立。

0 引 言

1 相关引理和定义

由文献[1]有引理1～引理3。

引理1 设M是n维完备非紧的黎曼流形，如果它的径向Ricci曲率不小于-(n-1)k/r2，那么∀α，0≤α≤1，有[1]

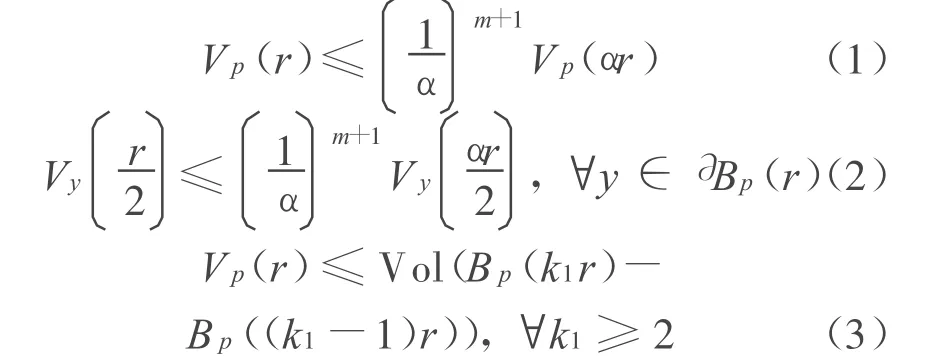
其中，k＞0;m=(n-1)(1+1+4k)/2;Vp(r)为以p为圆心、r为半径的测地球Bp(r)的体积。

定义1 曲率是渐近非负的，如果KM(x)≥-λ(r(x))，λ(◦)是在[0，+∞)上非负非增的函数，并且

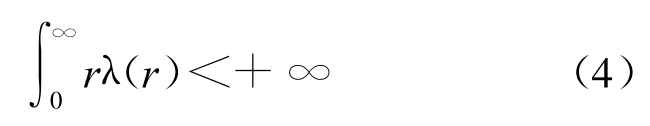
r(x)=dist(p，x)，并且p是M上的一个固定的点。

引理2 假设M是一个完备非紧的流形，有渐近非负的曲率，那么∀r≥0，0≤α≤1，有[1]

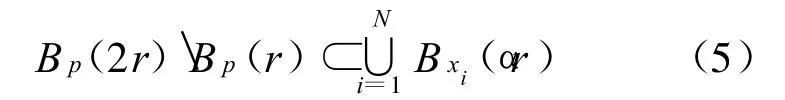
其中，xi∈Bp(2r)Bp(r)，并且N是一个与r无关的正整数。

由于式(18)中的模型似然函数是通过局部测量和局部测量单元的估算计算的,因此，如果有多个传感器测量可用,可以通过融合其他局部模型似然函数来更新.每个动作模式的更新局部似然函数表示为累积似然函数，即

引理3 设M是一个完备非紧的黎曼流形，有渐近非负的曲率，那么存在一个正整数C D＜∞，使得∀x∈M，∀r≥0，则有:

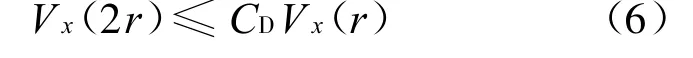
设M是一个完备非紧的黎曼流形，给M上任意函数f≥0，定义

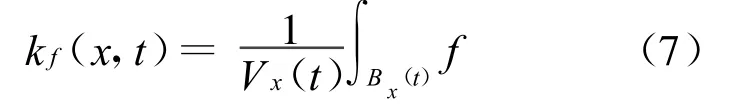
设M是一个完备非紧的有渐近非负的曲率的黎曼流形，考虑Poisson方程Δu=f。

由文献[2]有引理4、引理5。

引理4 设M是一个完备非紧的有渐近非负的曲率的黎曼流形，如果M是非抛物的，对所有的x≠y，Green函数满足

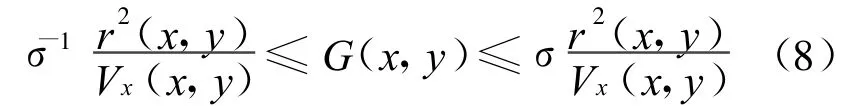
其中，σ是一个常数。

设f≥0是一个局部 H¨older连续函数，且k(x，t)=kf(x，t)，k(t)=k(o，t)，o是一个固定的点，假设∫∞0k(x，t)d t＜∞，Poisson方程Δu=f有一个解u，且适合u(o)=0与不等式:

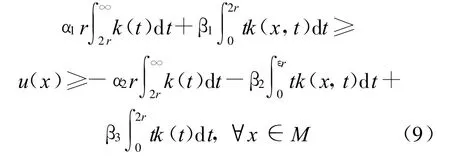
其中，αi(n，σ)(i=1，2)和βi(n)(i=1，2，3)为常数;r=r(x)表示从o点到x点的距离。

引理5 设M是一个完备非紧的有渐近非负的曲率的黎曼流形，f≥0是一个局部H¨older连续函数，k(x，t)=kf(x，t)，k(t)=k(o，t)，o是一个固定的点，假设∫∞0 k(x，t)d t＜∞，并且存在1＞δ＞0，h(t)≥0，0≤t＜∞，h(t)=o(t)，对所有的x和对所有的t≥δr(x)，当t→∞，使得

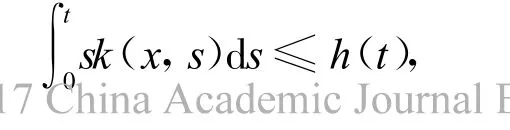
那么Poisson方程Δu=f有一解u，即

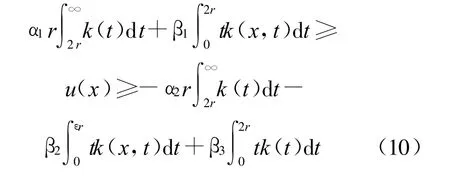
其中，αi(n，σ)(i=1，2)和βi(n)(i=1，2，3)为常数;|u(x)|=o(r(x))，r→∞。

2 定理及证明

定理1 设M是一个完备非紧的有渐近非负的曲率的黎曼流形，f≥0是一个局部H¨older连续函数，k(x，t)=kf(x，t)，k(t)=k(o，t)，o是一个固定的点，假设∫∞0 k(x，t)d t＜∞，令u是在引理4得到的Δu=f的解，那么

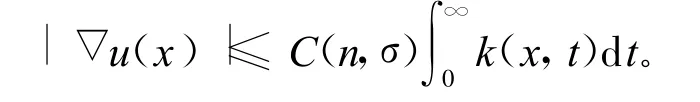
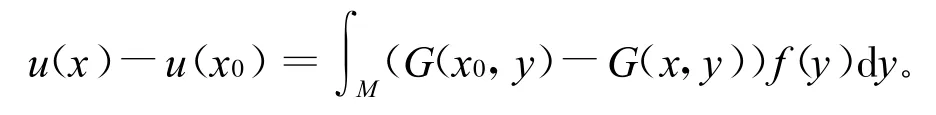
由引理3和引理4的证明[1，2]可得:

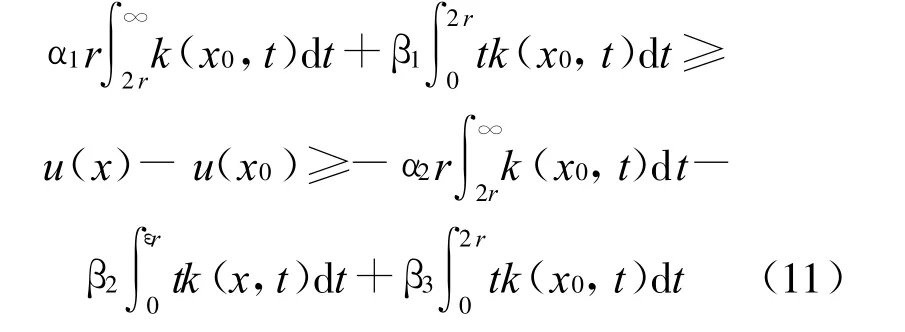
其中，αi、βj是引理4或引理5中的常数;r= r(x，x0)。选择ε=1/4，对(11)式两边除以r且r→0，则得定理1成立。

定理2 设M是一个完备非紧的有渐近非负的曲率的黎曼流形，f≥0是一个局部H¨older连续函数，k(x，t)=kf(x，t)，k(t)=k(o，t)，o为一个固定的点，假设∫∞0 k(x，t)d t＜∞，令u为在引理4得到的Δu=f的解，对任意的p≥1和α≥2，那么

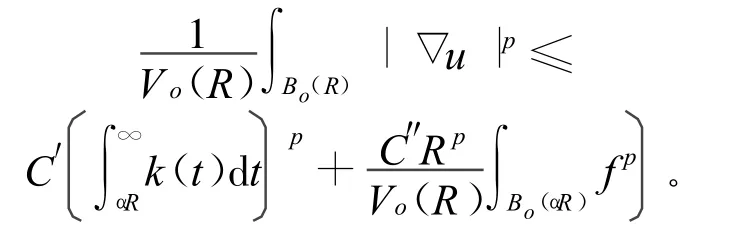
证明 对任意的x∈Bo(R)，有

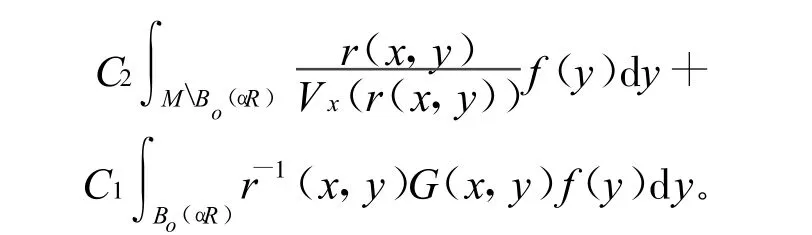
利用文献[6]的梯度估计有:

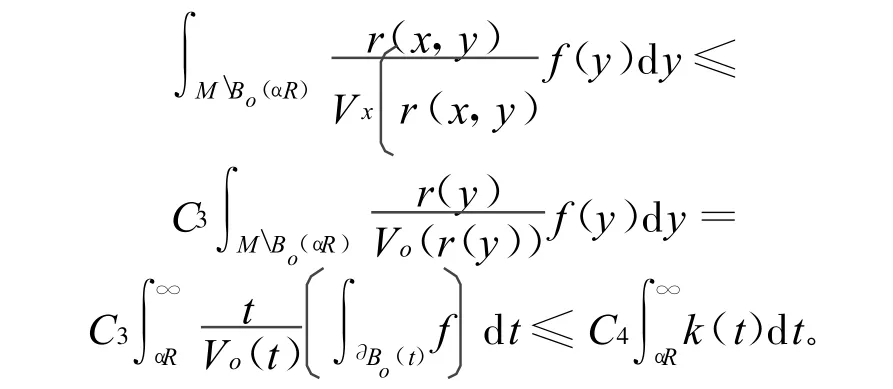
假设p＞1，令q=p/(p-1)，因此可得:

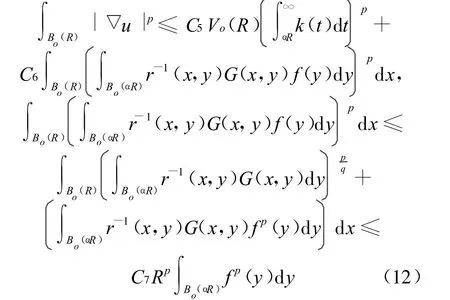
综合(12)式可得结论成立。

定理3 设M是一个完备非紧的有渐近非负的曲率的黎曼流形，f≥0是一个局部H¨older连续函数，k(x，t)=kf(x，t)，k(t)=k(o，t)，o是一个固定的点，假设∫∞0 k(x，t)d t＜∞，令u是在引理4得到的Δu=f的解，那么

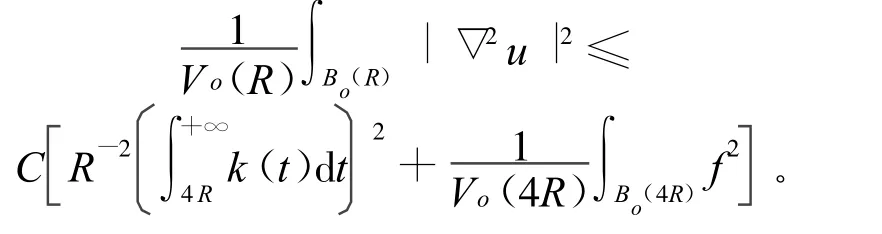
证明 由局部标架公式

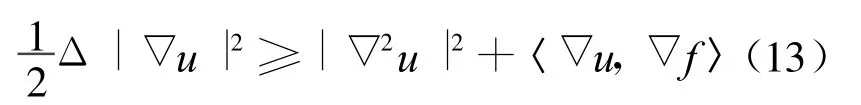
令φ是Bo(2R)上的光滑的紧的支撑函数，在(13)式两边乘以φ2并分部积分得:

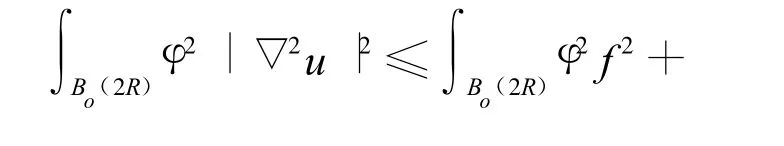
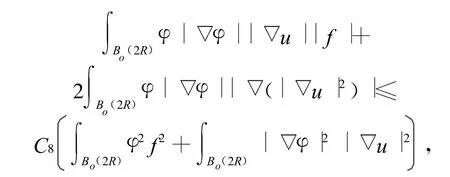
选择合适的φ可得:

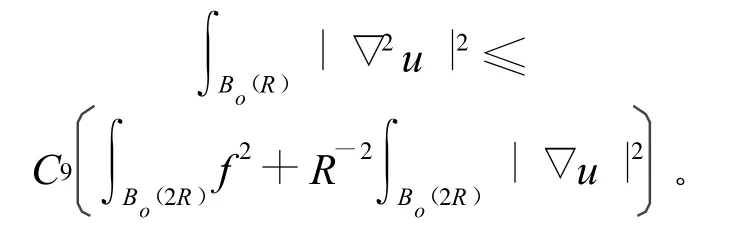
结合引理5可知结论成立。

[1] Zhou C H，Chen Z H.H armonic fun ctions on a com plete noncompactmanifold with asym ptotically nonnegative cu rvatu re[J].Ann Math，2004，25(4):523-532.

[2] 赵成兵，阮其华.关于Poisson方程解的一个注记[J].同济大学学报:自然科学版，2006，34(5):694-697.

[3] Cheng S Y，Yau S T.Differential equation on Rimannian manifold and their geom etric application[J].Comm Pure Apply Math，1975，28:333-354.

[4] Ni L，Yu G S，Tam L F.Poisson equation，Poincaré-Lelong equation and decay on complete K¨ahler manifold[J].Jou rnal of Differential Geometry，2001，57:339-388.

[5] Ni L.Vanishing theorem son complete K¨ahlermanifoldsand their ap plications[J].Journal of Differential Geometry，1998，50:89-122.

[6] Li P，Yau S T.On the parabolic kernel of the Schr¨odinger operator[J].Acta Math，1986，156:139-168.

[7] Li P，Yau S T.Curvatu re and holomorphic mappings of com plete K¨ahler m anifolds[J].Com postitio Mathematica，1990，73(2):125-144.

[8] M ok N，Siu Y T，Yau S T.The Poin caré-Lelong equation on complete K¨ahler manifolds[J].Compositio Mathematica，1981，44:183-218.

[9] 赵成兵，俞能福.一个关于K¨ah ler平坦的定理[J].合肥工业大学学报:自然科学版，2008，31(9):1528-1531.