解非线性方程的一种新的全局快速算法

倪 健， 马昌凤

(1.南京荣飞科技有限公司，江苏南京 210009;2.桂林电子科技大学数学与计算科学学院，广西桂林 541004;3.福建师范大学数学与计算机科学学院，福建福州 350007)

工程实际与科学计算中都遇到大量求解非线性方程f(x)=0的问题。对于这类问题，常常不能用解析方法求其精确解，而只能利用数值方法求其近似解。有关学者已提出求解非线性方程的许多数值方法[1-5]，牛顿法是最流行的一种解法[6]。但对于某些非线性方程，用牛顿法进行迭代求根需迭代多次。本文提出了解非线性方程的一种新方法，该方法通过对一些参数的选取，不仅比牛顿法收敛更快，而且具有全局收敛性。

1 解非线性方程新算法的描述

1.1 收敛性分析

设非线性方程为f(x)=0，其中f(x)为连续

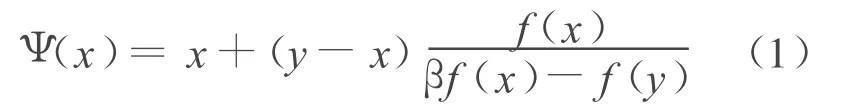
其中，y=x-αf(x)/f′(x)，0＜α≤1。

假设函数 f:R→R存在零点x*，且初始点x0在U(x*)内。欲使该迭代函数收敛，则需满足|Ψ′(x)|＜1，因此，本文首先计算Ψ′(x)，即可微的非线性函数。

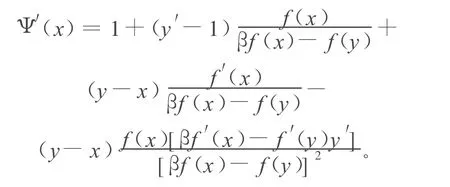
考虑迭代函数:

易知f(x*)=0，则有以下极限存在:

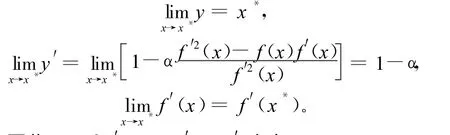
由此可得:

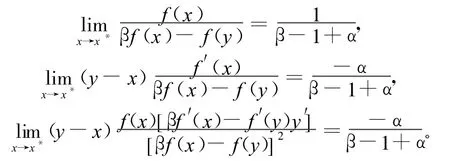
综上所述，可得:利用拉格朗日定理得:

即Ψ(a)-Ψ(b)=Ψ′(ξ)(a-b)，ξ∈(a，b)。所以|。

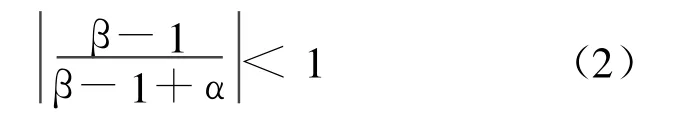
1.2 收敛效率分析

为简单起见，假设 f(x)＞0，f′(z)＞0，f″(z)＞0，z∈U(x*)。要使该方法的收敛速度优于牛顿法，则需在假设情况下，此方法一步收敛结果比牛顿法一步收敛结果更接近零点，即

x*≤Ψ(x)≤x-f(x)/f′(x)。

考虑:

当x→x*时，对两边取极限，有。考虑:

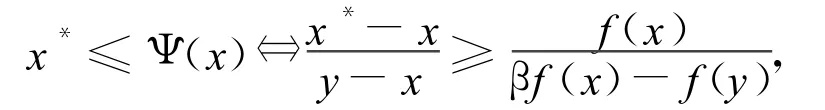
当x→x*时，对两边取极限，则有:

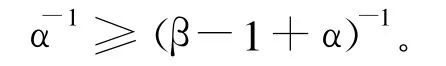
综上所述，(β-1+α)-1=α-1⇔β=1，代入(2)式有:

由此可得迭代函数:

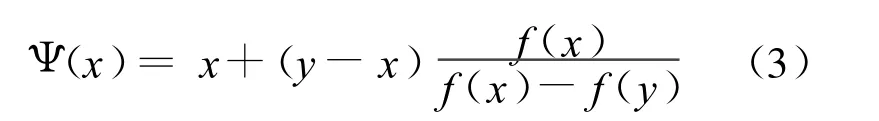
其中，y=x-αf(x)/f′(x)，0＜α≤1。所以此迭代函数较牛顿法有更快收敛速度。

2 全局参数描述

其中，y=x-αf(x)/f′(x)，0＜α≤1。

假设f(x)＞0，f′(z)＞0，f″(z)＞0，z∈U(x*)，在类似的情况下，其它情况同理可得。

为了使γ满足x*≤Ψ(x)≤y，考虑

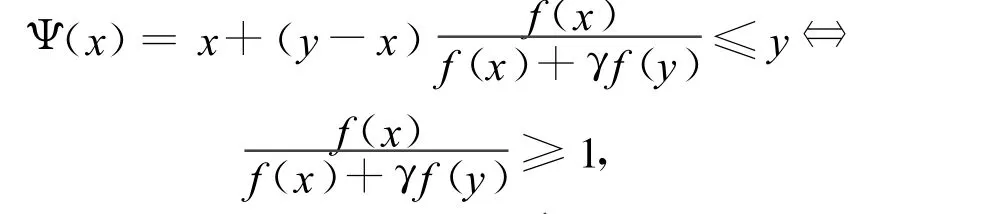
上述迭代函数不满足全局收敛。为了得到一个全局收敛的迭代函数，本文考虑以下迭代格式:

考虑:

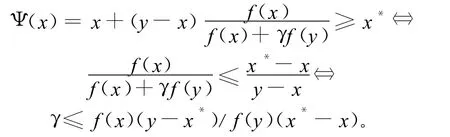
当x→x*时，对右边取极限，则有:

当γ=-1时，所考虑的迭代函数即为(1)式所示函数。

如果x0∉U(x*)，可以考虑

若f′(y)≈[f(y)-f(x)]/(y-x)，则有:

实际上，常用

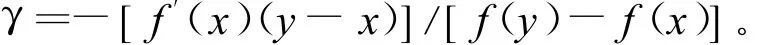
总结上述结果得到满足全局收敛的迭代格式为:

当|f(xk)|≤η，γ=-1。

3 算 法

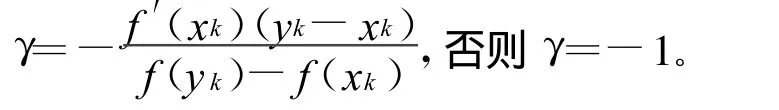
(4)计算 xk+1=xk+(yk-xk)f(xk)]/ [f(xk)+γf(yk)]。

(5)如果k＞n，停止;如果|f(xk)|＜ε，停止。

(6)k→k+1，返回步骤(2)。

根据上述论证，可得本文算法步骤如下:

(1)选取初始值x0∈R，α∈(0，1]，ε＞0，η＞0，n∈N，令k=0。

(2)计算yk=xk-αf(xk)/f′(xk)。

(3)如果|f(xk)|＞η，则

4 数值实验

为了验证本文算法的有效性，本文选取比较典型的代数方程和超越方程，在Matlab环境下进行数值模拟。

先将本文算法与牛顿法作比较，验证本文算法较牛顿法有更快收敛速度。实验方程如下:

例1 f(x)=(x-6)5-10(x-6)4+38(x-

6)3-68(x-6)2-57(x-6)-8=0;

例2 f(x)=1-exp(x2-3x-4);

例3 f(x)=x2-sin x;

例4 f(x)=exp(-x2)-ln(x+1)。

为了便于处理，设定参数分别为:容许误差ε=1.0E-11，n=1 000，η=0.1，α=1。实验结果见表1所列。

表1 数值实验结果

数值实验表明，本文算法的收敛速度明显快于牛顿法，平均减少1/2的迭代次数，且本文算法的全局收敛效果良好。

以上述例1和例3为算例，初始值x0分别取-10、-2.9，结果见表2所列。

表2 不同算例的收敛效率

数值实验表明，当α=1时，本文算法的迭代效果最佳。

5 结束语

本文介绍的新算法具有收敛速度快、计算精度高、计算精度可控、收敛性不依赖初始值的选择等特点，因此，本文算法不仅是有效的，而且是高效的。

[1] He JH.Improvement of New ton iteration method[J].Int J Non linear Sci Numer Simulation，2000，1(2):239-240.

[2] U jevic＇N.A m ethod for solving nonlinear equations[J].Appl M ath Comput，2006，174(2):1416-1426.

[3] 李声锋.求解方程的一类迭代方法及应用[D].合肥:合肥工业大学数学学院，2007.

[4] 林 洋，杨利华，詹棠森.预测校正磨光算法及应用[J].合肥工业大学学报:自然科学版，2010，33(8):1274-1276.

[5] 王能超.算法演化论[M].北京:高等教育出版社，2008: 35-59.

[6] Yamamoto T.Historicaldevelopment in convergence analysis for New ton's and New ton-like methods[J].JCom put ApplM ath，2000，124:1-23.