广义NNV方程组的新精确解和孤立波解
2011-03-15苗宝军梁庆利
苗宝军, 梁庆利
(许昌学院数学科学学院,河南许昌 461000)
构造非线性发展方程的精确解是非线性科学的重要研究内容。孤立波作为非线性科学中的一类重要的物理现象,长期以来成为众多专家学者研究的热点问题,而寻找各种精巧求解方法和获取新精确解及孤立波解则更成为非线性发展方程领域的研究热点之一。目前已有许多行之有效的方法可用于寻找显式精确解和孤立波解[1-7],如双曲函数法、符号计算代数法、混合指数法、齐次平衡法、F-展开法和扩展的Riccati映射法等。最近,由文献[8]创立了(G′/G)展开法,并成功应用于求解低维非线性发展方程的精确解。本文的主要工作是受益于文献[8]创立的(G′/G)展开法的启发,把它推广应用到高维非线性发展方程的求解。
本文研究了一类广义Nizhnik-Novikov-Veselov(简称 NNV)方程组的精确解和孤立波解,即
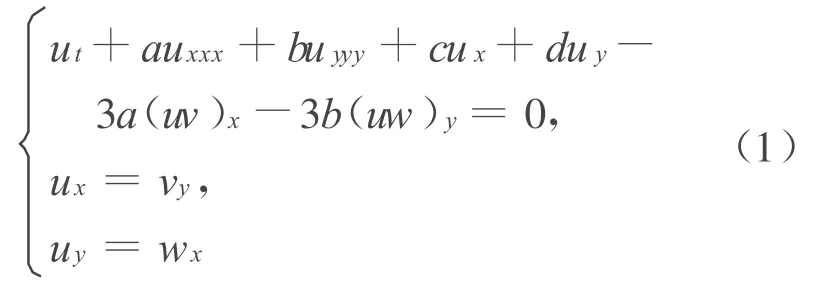
其中,a、b为非零常数;c、d为任意常数。(1)式模型受到了众多学者的广泛关注和研究[9-12]。
文献[9]用F-展开法获得了该系统的雅可比椭圆函数表示的周期波解,且在极限情况下获得了系统的一些类型的行波解;文献[10]利用拓展的Riccati方程映射法与变量分离法,得到了(2+ 1)维广义Nizhnik-Novikov-Veselov(GNNV)系统新的含有2个任意函数的相当广义的变量分离严格解,并简要讨论了其演化行为;文献[11]利用一种基于符号计算的代数方法,用F-展开法求解(2+1)维NNV方程组,获得了新的显式行波解;文献[12]通过运用多线性分离变量法所得方程解中含有任意函数这一特点,引入了符合原方程条件的Jacobi椭圆函数和Weierstrass椭圆函数,构造了(2+1)维广义NNV方程的新双周期解等。本文主要用扩展的(G′/G)-展开法,结合齐次平衡方法的思想原则,获得了(1)式的3种形式的新精确行波通解和孤立波解。
1 扩展(G′/G)-展开法
根据文献[8]提出的(G′/G)-展开法对其推广,使其适用于高维非线性方程的情形,得到扩展后的(G′/G)-展开法。给定含独立变量x,y,z,…,t非线性偏微分方程为:
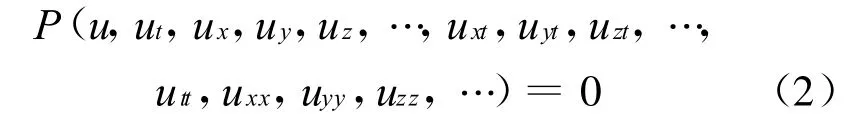
其中,P为u及其u关于x,y,z,…,t各阶偏导数的多项式,且含高阶偏导数项和非线性项。扩展(G′/G)-展开法求解的步骤如下:
(1)对(2)式行波约化,令
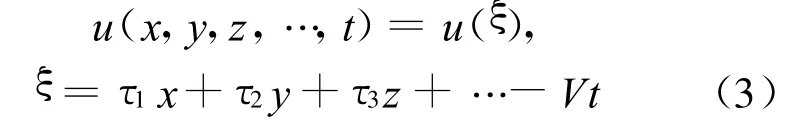
其中,V为待定常数。
将(3)式代入(2)式,得到u(ξ)的常微分方程为:

(2)设(4)式的解可表示为(G′/G)的多项式:
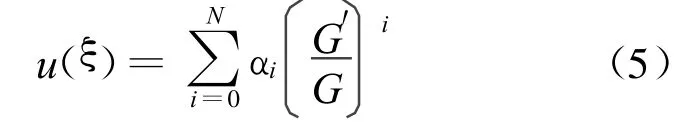
其中,αN≠0,αN,…,α0为待定常数,正整数N由(4)式中具有支配地位的非线性项和最高阶导数项齐次平衡确定;G=G(ξ)满足二阶线性常微分方程ODE,则有:
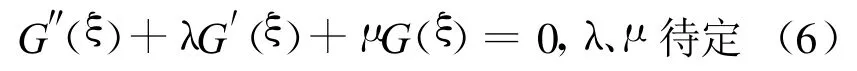
(3)将(5)式代入(4)式,并运用(6)式合并(G′/G)的相同幂次项,方程的左端变成一个关于(G′/G)的一个多项式,令该多项式的(G′/G)各阶幂次的系数为零,导出关于αN,…,α0,τi,V,λ,μ的非线性代数方程组。
(4)解上述代数方程组,将所得结果以及(6)式不同情况下的通解代入(5)式,可得(2)式多个精确行波解。
2 广义NNV方程组的精确解和孤立波解
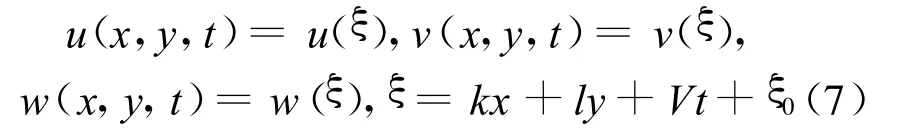
如果令:将(7)式代入(1)式,则有:
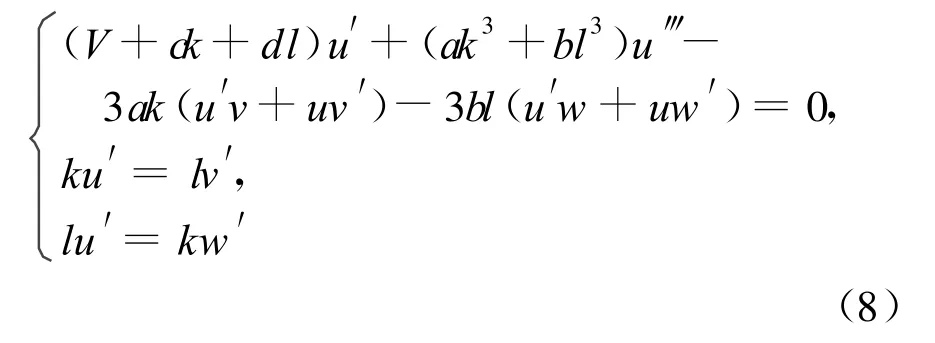
对(8)式中各等式关于ξ积分一次并令积分常数为零,进行计算整理得到:
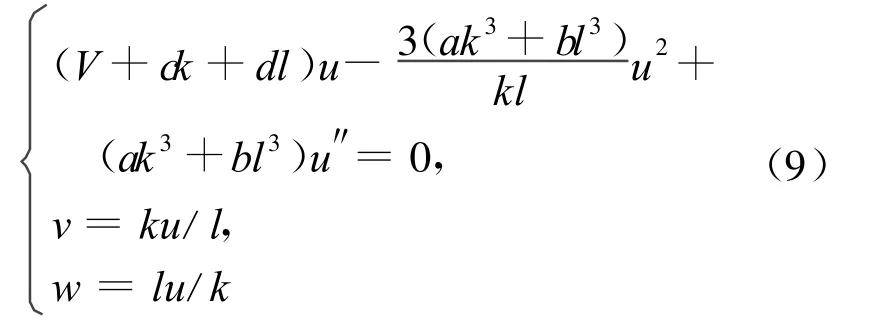
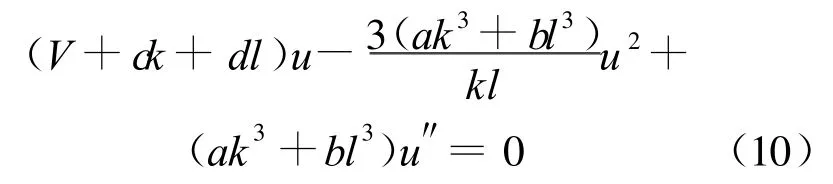
考虑(10)式中的最高阶导数项u″与最高次非线性项u2的齐次平衡,有N+2=2N,可确定(5)式中的N=2。因而可设(10)式的解为:
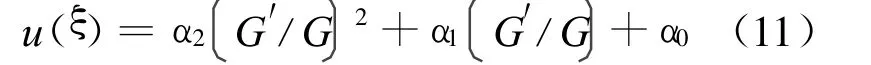
其中,α2≠0,α0,α1,α2为待定的常数;G=G(ξ)满足二阶线性常微分方程(6)式。于是有:
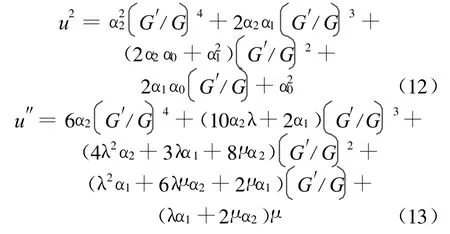
因此,为了求出系统的精确解和孤立波解,只需先求出方程的精确行波解和孤立波解,即
将(11)~(13)式代入(10)式,合并(G′/G)的同次幂项并置其系数为零,进行计算整理可得到关于α0,α1,α2,λ,μ,k,l,V的非线性代数方程组为:
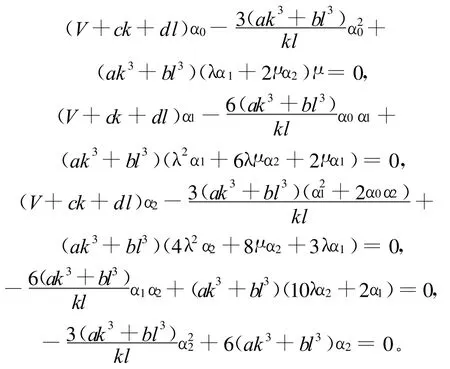
解以上非线性代数方程组得:
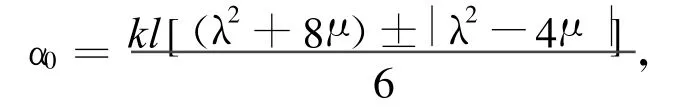
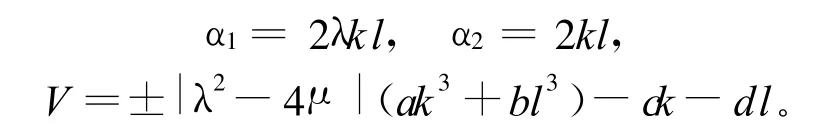
所以(10)式的解可表示为:
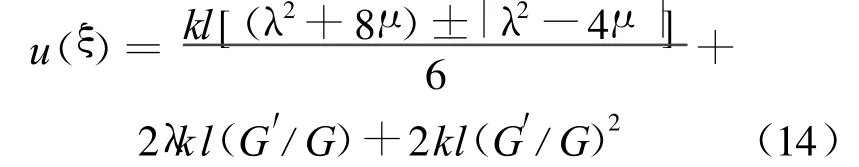
下面对λ2-4μ的取值分3种情形讨论,求出(1)式的精确解和孤立波解。(1)当λ2-4μ>0时,有
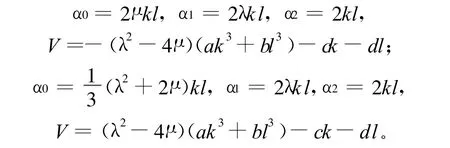

且有:其中,c1、c2是任意常数。
将(15)式、(16)式代入(14)式,即可得到(1)式的2组精确通解(17)式和(18)式。(17)式中,ξ=kx+ly+[(λ2-4μ)(ak3+b l3)-ck-d l]t+ ξ0,(18)式中,ξ=k x+ly+[-(λ2-4μ)(ak3+ b l3)-ck-d l]t+ξ0。

〛特别地,取c1=0,c2≠0,μ=0,λ>0,通解(17)式和(18)式分别变为(1)式的2组孤立波解,其中一组弧立波解为:

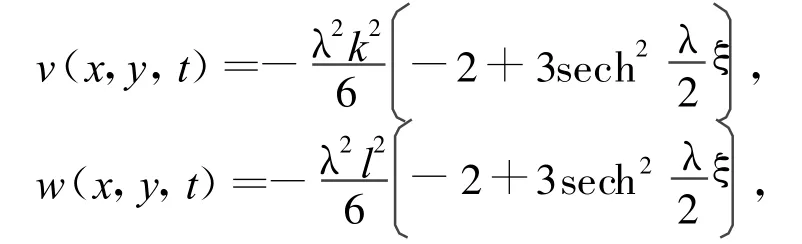
其中,ξ=kx+ly+[λ2(ak3+bl3)-ck-d l]t+ξ0。另一组弧立波解为:
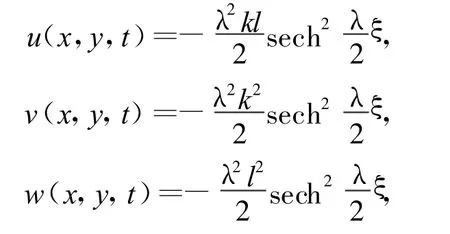
其中,ξ=kx+ly+[-λ2(ak3+b l3)-ckd l]t+ξ0。
(2)当λ2-4μ<0时,有
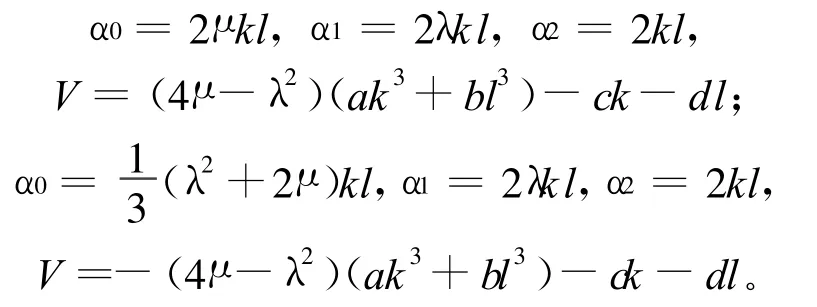
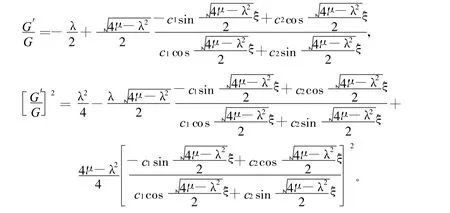
于是可得(1)式的2组三角函数通解(19)式和(20)式。(19)式中ξ=kx+ly+[(4μ-λ2)×(ak3+ bl3)-ck-d l]t+ξ0,(20)式中ξ=kx+ly+ [-(4μ-λ2)(ak3+bl3)-ck-d l]t+ξ0。

(3)当λ2-4μ=0时,有
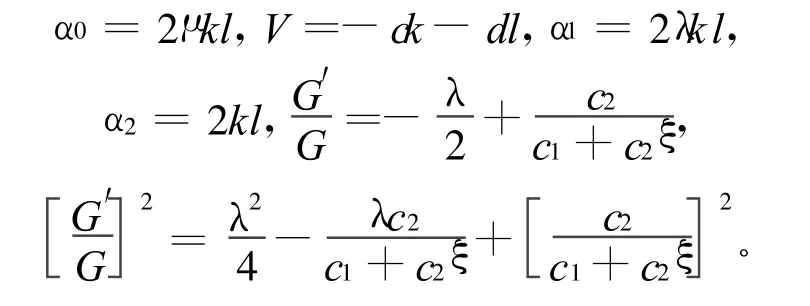
于是可得(1)式的有理函数通解为:
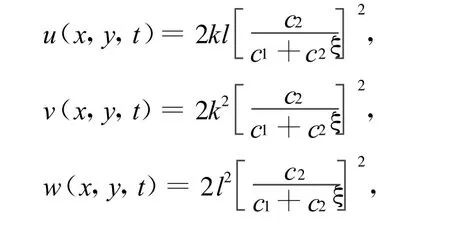
其中,ξ=kx+ly+[-ck-d l]t+ξ0。
3 结束语
本文主要利用扩展的(G′/G)-展开法,结合齐次平衡方法中的思想原则对一类广义非线性发展方程NNV进行求解,求出了该方程组新的精确通解和孤立波解,丰富了该方程组的解系。从求解过程易知:此方法不仅简单易操作可行,而且也可用来解决其它的高维非线性数学物理方程的精确解和孤立波解。
[1] Yang L,Liu J B,Yang K Q.Exact solutions of nonlinear PDE,nonlinear transfo rm ations and reduction of nonlinear PDE to a quadrature[J].Phys Lett A,2001,278:267-270.
[2] 李志斌.非线性数学物理方程的行波解[M].北京:科学出版社,2007:96-112.
[3] 徐桂琼,李志斌.构造非线性发展方程孤波解的混合指数方法[J].物理学报,2002,51(5):946-950.
[4] W ang M L.Solitary w ave solutions for variant Boussinesq equations[J].Phys Lett A,1995,199:169-172.
[5] Shen JW,Xu W.Bifurcations of smooth and non-smooth travellimg w ave solu tions of the Degasperis-Procesi equation[J].In t JNonlinear SciSimul,2004,5(4):397-402.
[6] 苗宝军,容跃堂.耦合 Sch r¨odinger-Boussinesq方程组的行波解和分歧方法[J].合肥工业大学学报:自然科学版,2008,31(11):1918-1923.
[7] 张金良,王明亮,王跃明.推广的F-展开法及变系数KdV和mKdV的精确解[J].数学物理学报,2006,26A(3): 353-360.
[8] Wang M L,Li X Z,Zhang J L.The(G′/G)-expansion method and travelling w ave solutions of nonlinear evolu tion equations inm athematical physics[J].Phys Lett A,2008,372:417-423.
[9] Zhang J L,Ren K F,Wang M L,et al.Theperiodicw ave solutions for the generalized Nizhnik-Novikok-Veselov equation[J].Chinese Physics,2003,12(8):825-830.
[10] 朱海平,郑春龙.(2+1)维广义Nizhnik-Novikov-Veselov系统的新严格解和复合波激发[J].物理学报,2006,55 (10):4999-5006.
[11] 傅海明,戴正德.(2+1)维Nizhnik-Novikov-Veselov方程组的新精确解[J].山东师范大学学报:自然科学版,2009,24(3):15-21.
[12] 豆福全,孙建安,黄 磊,等.(2+1)维广义Nizhnik-Novikov-Veselov方程的新周期波、局域激发之间的相互作用[J].西北师范大学学报:自然科学版,2007,43(3): 27-33.
