一种快速计算阻抗矩阵的有效方法
2011-03-15胡怀宏孙玉发
胡怀宏, 孙玉发
(安徽大学电子科学与技术学院,安徽合肥 230039)
矩量法是一种数值精确解,在分析电磁辐射和散射问题中得到广泛应用。但是,对于电大尺寸目标,采用传统矩量法进行数值求解时,在计算机内存占用量和计算量2方面都存在不可逾越的困难。因此,寻求快速求解矩量法阻抗矩阵元素的新方法成为计算电磁学领域的研究热点之一。目前减少阻抗矩阵填充时间的方法主要有快速多极子算法(FMM)[1,2]、多层矩阵分解算法(M LMDA)[3]、阻抗矩阵局部化法(IM L)[4]和小波基展开法[5,6]等。
本文以矩量法和RWG基函数[7]为基础,在阻抗矩阵元素的计算中,将源点处的三角单元划分成9个完全一样的小三角块,这样阻抗元素计算中的双重积分就可以用求和来代替,进而可以加速阻抗矩阵元素的填充。
1 理论分析
1.1 电场积分方程
平面波按照一定角度入射到导体表面,根据导体表面切向电场为零,可得电场积分方程为:
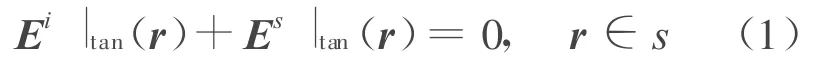
其中,Es为导体表面电流J产生的散射场,可以表示为:
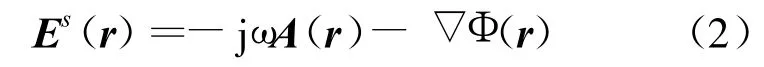
其中,矢量磁位A和标量电位Φ与表面电流之间的关系如下:
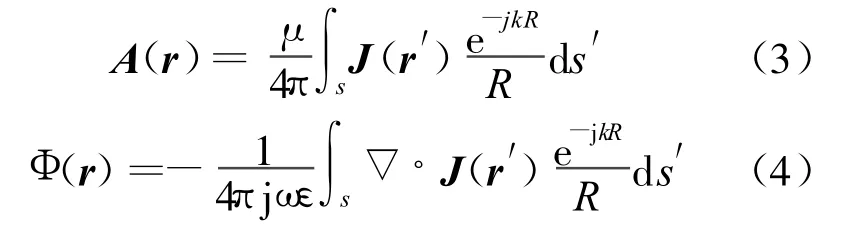
应用矩量法求解电场积分方程,表面电流J(r)用RWG基函数f n(r)展开[7]为:
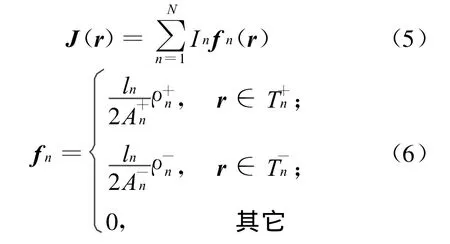
其中,In为第n个基函数的系数;N为未知变量数;ln为2个三角单元公共边长度;A±n为三角单元的面积;rc±n为原点到三角单元质心的位置矢量;ρc+n为三角单元 T+n中自由顶点到质心的距离矢量;ρc-n为三角单元T-n中质心到自由顶点的距离矢量。RWG边元示意图,如图1所示。
将(5)式代入(1)式,采用伽略金法,可得阻抗矩阵元素为:
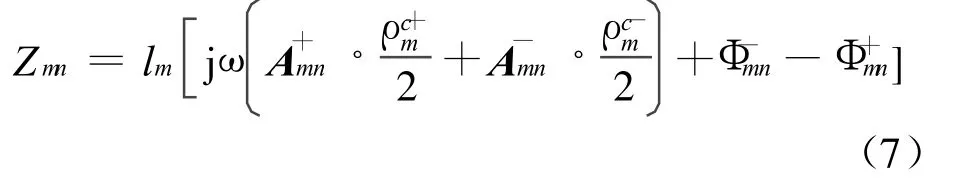
其中
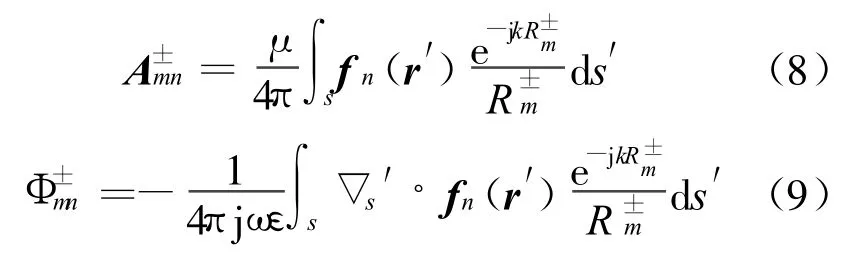
m-r′|表示场点到源点的距离。
1.2 质心切分法
阻抗矩阵元素中的双重积分,一般采取高斯积分来计算,但是高斯积分取点多,计算效率低。
本文采取质心切分法将任意一个面积为 An的三角单元剖分成若干个完全一样的小三角块。由于剖分后的三角块足够小,被积函数在每个小三角块上近似为常数,可以用求和来计算阻抗矩阵元素中的双重积分[8],减少阻抗矩阵元素的填充时间。在计算阻抗矩阵元素时,场点总是近似取在三角单元的质心,源点近似取在每个小三角块的质心。如图2所示,空心圆圈表示三角单元质心,实心黑点表示每个小三角块的质心rkc。
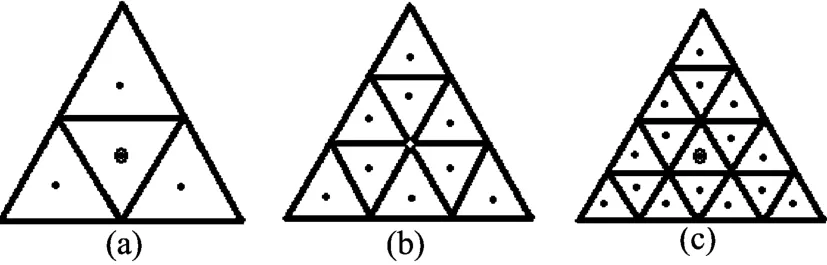
图2 三角单元质心剖分示意图
以图2b为例来说明质心切分法的实现过程。假设被积函数在每个小三角块上为常数,那么,函数g在原始三角单元An上的积分可以表示为[9,10]:
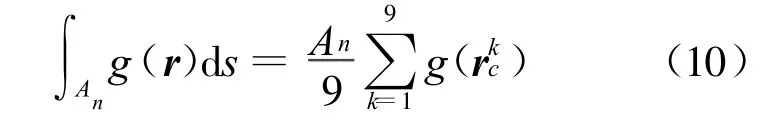
由图1可以看出:
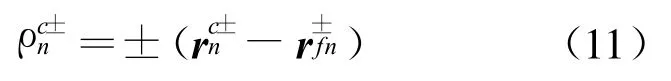
根据(10)式、(11)式,(8)式、(9)式可以表示为:
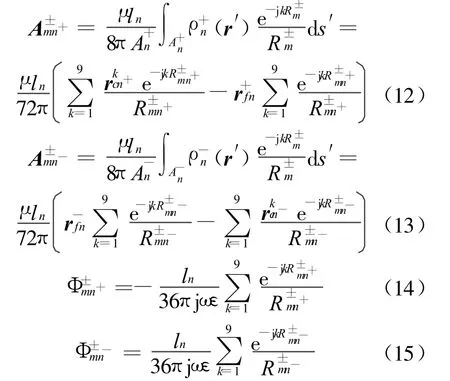
将(12)~(15)式代入(7)式便可快速求出阻抗矩阵元素。若采用图2a、图2c的剖分方式计算阻抗矩阵,不可避免地会在其中一个小三角块上出现R±mn±→0的情况,所以采取图2b的剖分是最理想的情况。应用图2b的质心切分法计算阻抗矩阵,不会出现场点与源点重合的奇异情况,因此在计算时不用区分奇异解和非奇异解情况,从而大大减少了计算量。
2 数值结果分析
为了验证本文方法的效率及准确性,首先计算了长和宽为3 cm×2 cm的导体平板的双站RCS。入射平面波沿θi=90°、φi=0°的角度入射,入射频率为22 GHz。平板被剖分成1 200个三角单元,共有1 750个未知变量。传统矩量法和质心切分法计算的双站 RCS曲线如图3所示。从图中可以看出质心切分法的计算结果与传统矩量法计算结果吻合良好。由于传统矩量法计算阻抗矩阵元素必须在每个三角对上计算3个独立的双重积分,程序中所设变量多,步骤复杂;而质心切分法在计算时不需计算任何积分,编程时只需计算简单的求和,所需变量少,程序简单。在程序中对2种方法阻抗矩阵的填充时间进行统计,分别为17.2 s和24.7 s,可见质心切分法阻抗矩阵填充时间比矩量法节约了30.4%。
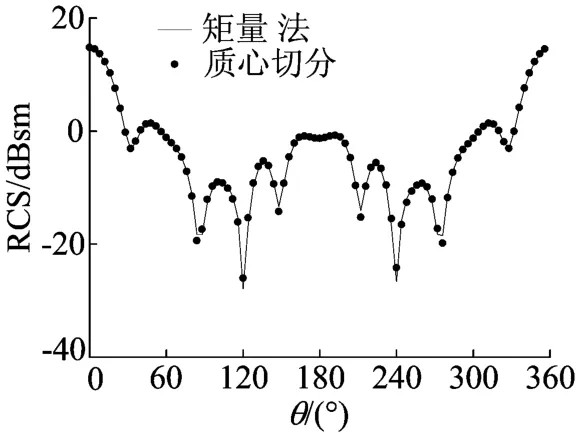
图3 导体平板的双站RCS
其次计算了导体球的双站RCS。导体球的半径为0.8 cm,被剖分成2 000个三角单元,共有3 000个未知变量,其它参量与前一个算例相同。传统矩量法和质心切分法计算的双站 RCS结果如图4所示。
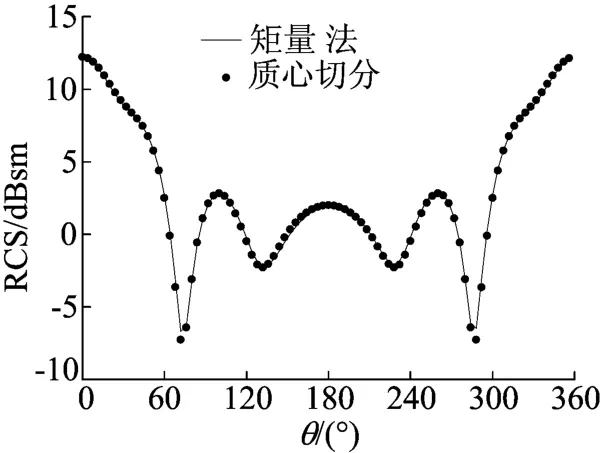
图4 导体球的双站RCS
由图4可见两者吻合良好,且应用质心切分法阻抗矩阵填充时间为53.8 s,而传统矩量法需要94.1 s,前者比后者时间节省了42.8%。数值计算表明,当导体电尺寸越大,未知变量数越多时,质心切分法的计算效率越高。
本文采用Fortran语言编写程序,所有计算都在Pentium4、1.00GB内存的PC机上完成。
3 结束语
将质心切分法用于研究导体目标电磁散射特性,不仅能简化计算过程,而且能够大幅度地减少阻抗矩阵填充时间,具有较高的计算效率。与其它快速算法相比,质心切分法具有编程简单、易于与传统矩量法软件集成等优点。本文方法还可以推广到复杂目标电磁散射特性的快速分析中。
[1] Coifman R,Rokhlin V,Wandzu ra S.The fast m ultipole method for the w ave equation:a pedestrian p rescription [J].IEEE An tennas and Propagation M agazine,1993,35 (3):7-12.
[2] 樊振宏,丁大志,陈如山.多层快速多极子技术分析微带天线[J].电波科学学报,2008,23(2):235-238.
[3] Rius J M,Parron J,Ubeda E,et al.Multilevel matrix decomposition algorithm for analysis of electrically large electromagnetic problem s in 3-D[J].M icrowave and Optical Technology Letters,1999,22(3):15-26.
[4] Canning F X.Im proved impedan ce matrix localization method[J].IEEE Transactions on Antennas and Propagation,1993,41(5):659-667.
[5] 董 辉,朱义胜,赵柏山.基于小波矩量法的平面螺旋电感的电磁辐射研究[J].电子学报,2009,37(3):535-539.
[6] 林正英,时维元,张 伟.基于主成分和小波分析的复杂纺织设备系统的信号处理方法研究[J].合肥工业大学学报:自然科学版,2010,33(9):1285-1289.
[7] Rao SM,Wilton D R,G lisson A W.Electromagnetic scattering by su rfaces of arbitrary shape[J].IEEE T ransactions on Antennas and Propagation,1982,30(3): 409-418.
[8] Hussein K F A.Fast computationalalgorithm for EFIE applied to arbitrarily-shaped conducting surfaces[J].Progress In Electromagnetics Research,2007,PIER 68:339-357.
[9] Makarov S N.An tenna and EM modeling w ith M atlab [M].New York:John Wiley and Sons,2002:18-19.
[10] 楚玉焕,邢光龙,武永刚.计算RWG基函数阻抗矩阵的混合积分方程[J].电子测量技术,2008,31(9):25-27.
