环+上的一类常循环码

丁 健， 李红菊， 刘家保

(安徽新华学院数理部，安徽合肥 230088)

0 引 言

近年来，编码理论与密码学方向的学者对剩余类环Fq+uFq+…+uk-1Fq有浓厚的兴趣(q为素数p的方幂)。文献[1]研究了F2+uF2上的循环码，以及(n，2)=1时(1+u)常循环码及其G ray像;文献[2]利用环Fq+uFq上的线性码进行了格的构造;文献[3]给出了环Fq+uFq上关于厄米特内积的线性码的自对偶码计数公式;文献[4]利用环Fq+uFq上的码，通过线性码的G ray映射找到了一大批Fq上的最优码;文献[5]探讨了环Fp+uFp+…+uk-1Fp上的准循环码;文献[6]研究了n=pe时，环Fq+uFq+…+ uk-1Fq上的(1+αu)常循环码的结构;文献[7]讨论了Fpk+uFpk上的(1-u)常循环码;文献[8]研究了F2+uF2的伽诺瓦扩环上长为2s的所有常循环码。本文研究了(n，p)=1时，Fpk+uFpk上的一类常循码的置换等价性及其 Gray像的结构。

1 基本概念

令p是素数且k∈N，R代表环Fpk+uFpk，其中u2=0，Fpk=GF(pk)，则R是以uR和Fpk为极大理想的有限链环。令C为R上长为n的码，P(C)为其多项式，则

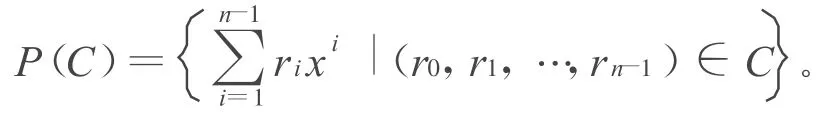
令V为从Rn到Rn的映射，即

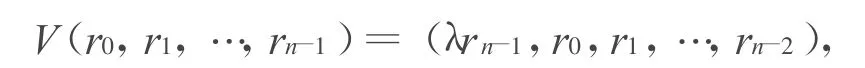
其中，λ为R上的单位。则有C是R上的λ常循环码⇔V(C)=C。

命题1 R上长为n的码C是λ常循环码⇔P(C)是R[x]/〈xn-λ〉的理想。

若ξ是Fpk上的一个本原元，则与ε∈Zpk相对应地有:

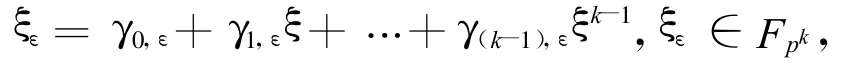
R上的Gray映射为有限链环上Gray映射的特例[3]，即

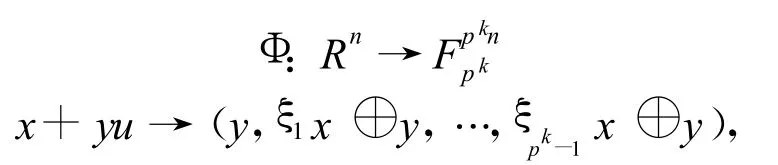
其中，⊕为Fpk上的分量相加。

2 (1+αu)循环码及其Gray像

假设(n，p)=1，则存在n′∈{0，1，…，p-1}满足nn′≡1(mod p)，与文献[9]类似，本文令β= 1+n′αu，作如下映射:

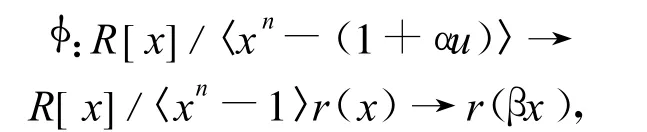
可得到以下引理。

引理 1 本文构造的 φ映射是从R[x]/〈xn-(1+αu)〉到R[x]/〈xn-1〉的环同构映射。

证明 对于任意f(x)，g(x)∈R[x]，

存在h(x)∈R[x]使得

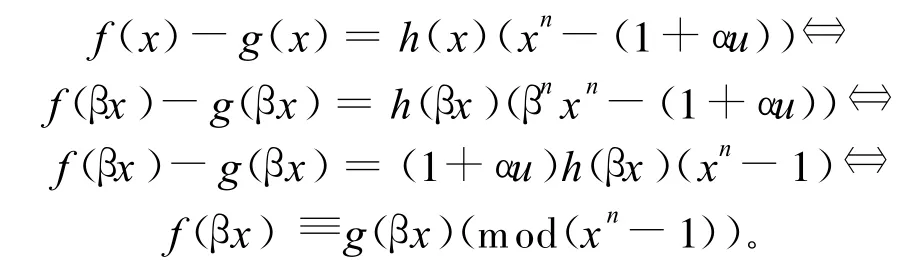
所以φ映射是从R[x]/〈xn-(1+αu)〉到R[x]/〈xn-1〉的一一映射。

由于φ(f(x)+g(x))=f(βx)+g(βx)= φ(f(x))+φ(g(x))，φ(f(x)g(x))= f(βx)g(βx)=φ(f(x))φ(g(x))，所以φ映射是从R[x]/〈xn-(1+αu)〉到R[x]/〈xn-1〉的环同构映射。

由引理1易得定理1。

定理1 若(n，p)=1，那么Fpk+uFpk上长为n的(1+αu)循环码彼此置换等价，其中α∈Fpk。

引理2 若(n，p)=1，那么Fpk+uFpk上长为n的循环码的G ray像彼此置换等价于Fpk上长为pkn、指数为pk-1的准循环码[4]。

由定理1及引理2可得推论1。

推论1 若(n，p)=1，那么Fpk+uFpk上长为n的(1+αu)循环码的Gray像彼此置换等价于Fpk上长为 pkn、指数为 pk-1的准循环码，其中α∈Fpk。

3 (ξi+αu)循环码及其Gray像

ξ是Fpk上的一个本原元，假设(n，p)=1且(n，pk-1)=1，那么存在n′∈{0，1，…，p-1}使得nn′≡1(mod p)，且方程nx≡i(m od(pk-1))存在唯一的解x=j∈Zpk-1，使得(ξj)n=ξi，令β′= ξj+n′ξ(1-n)jαu，作如下映射:

与引理1的证明类似，可得到引理3。

引理3 以上构造的 ψ映射是从R[x]/〈xn-(ξi+αu)〉到R[x]/〈xn-1〉的环同构映射。

由引理3可得定理2。

定理2 若(n，p)=1，且(n，pk-1)=1，那么Fpk+uFpk上长为n的(ξi+αu)循环码彼此置换等价，其中i∈Zpk，α∈Fpk。

由引理2可得推论2。

推论2 若(n，p)=1，且(n，pk-1)=1，那么Fpk+uFpk上长为n的(ξi+αu)循环码的Gray像彼此置换等价于Fpk上长为pkn、指数为pk-1的准循环码，其中i∈Zpk，α∈Fpk。

4 实例分析

令F4={0，1，ω，1+ω=ω2}，在F4+uF4中考虑n=5的循环码和常循环码。此时p=2，k= 2。因为(2，5)=1，对于(1+αu)循环码，α∈F4，可作映射:

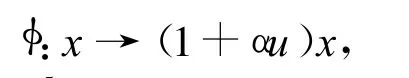
此时[(1+αu)x]5-(1+αu)=(1+αu)(x5-1)，从而验证了定理1。

特别地，(5，22-1)=1，对于(ω+αu)循环码，α∈F4，可作映射:

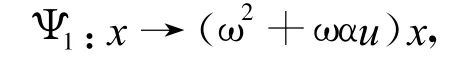
此时有:

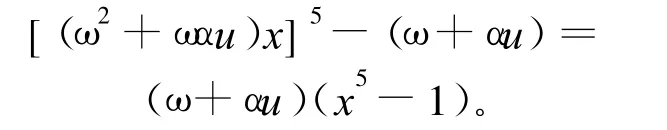
对于(ω2+αu)循环码，α∈F4，可作映射:

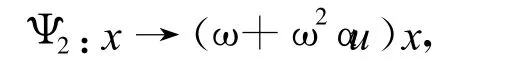
此时有:

从而验证了定理2。

5 结束语

本文研究了环Fp k+uFpk上长n与p互素时(1+αu)常循环码的置换等价性，研究了当(n，p)=1且(n，pk-1)=1时，(ξi+αu)常循环码的置换等价性，为进一步研究环Fpk+uFpk上的常循环码提供了便利。

[1] Qian JF，Zhang L N，Zhu S X.(1+u)-constacyc lic and cyclic codesover F2+uF2[J].Applied Mathematics Letters，2006，19(8):820-823.

[2] Bachoc C.A pplication of coding theory to the construction of modular lattices[J].Jou rnal of Combinational Theory: Series A，1997，78(1):92-119.

[3] Gaborit P.M ass formulas fo r self-dual codes over Z4and Fq+uFqrings[J].IEEE T ransactionson Information Theory，1996，42(4):1222-1228.

[4] Gu lliver T A，H arada M.Codesover F3+uF3and improvements to the bounds on ternary linear codes[J].Designs，Codes and Cryp tography，2001，22(1):89-96.

[5] 李富林，朱士信.环Fp+uFp+…+ukFp上的准循环码[J].合肥工业大学学报:自然科学版，2009，32(11): 1766-1768.

[6] 朱士信，李 平，吴 波.环Fq+uFq+…+uk-1Fq上一类重根常循环码 [J].电子与信息学报，2008，30(6): 1394-1396.

[7] Am ar ra M C，Nemenzo F R.On(1-u)-cyclic codes over Fpk+uFpk[J].Applied Mathematic Letters，2008，21:1129 -1133.

[8] Dinh H Q.Constacyclic codesof length 2sover galoisextension rings of F2+uF2[J].IEEE T ransactions on Information Theory，2009，55(4):1730-1740.

[9] Ling S，Blackfors J.Zpk+1-linear codes[J].IEEE transactions on Info rm ation Theory，2002，48(9):2592-2605.