炮膛内底排装置燃烧特性计算分析

张领科，余永刚，陆欣，李志锋

(1.南京理工大学 能源与动力工程学院，江苏 南京210094;2.总装备部驻724 厂军事代表室，辽宁 沈阳110045)

0 引言

底部排气弹(简称底排弹)与传统弹丸相比，在相同的初速条件下其射程可提高约20%～30%，故底排弹已在大口径火炮系统中得到了广泛的应用［1］。美国陆军弹道研究所自20 世纪90年代就深入开展了底排弹的飞行特性理论和测试的研究［2-3］，为底排弹的弹道计算分析奠定了基础。底排弹初速散布和底排药柱膛口质量偏差的随机性是造成底排弹射程散布偏大的重要因素之一。初速散布主要由火炮装药条件与底排药柱膛内燃烧特性决定;底排药柱膛口质量偏差的随机性除了与底排药柱膛内受到高温高压燃气的冲击—变形—脱落有关外，也与底排药柱膛内燃烧特性有关。

底排药柱在火炮膛内的燃烧情况很难用试验方法测得。为此，通过针对某底排药剂的密闭爆发器燃烧试验数据进行整理分析，得到其高压工况下的燃速模型;根据底排装置在火炮膛内点火直至全面燃烧的特点，建立底排装置膛内发射过程中燃烧模型与适用于底排弹的零维火炮内弹道模型;采用数值模拟的方法联立耦合求解上述两个模型，研究火炮内弹道过程中底排装置燃烧室内的压力、喷口质量流量及底排药剂燃烧量等的变化情况，可为分析底排弹出膛口瞬间药柱质量偏差引起的射程散布提供基础数据。

1 高压底排药柱燃速模型

底排药剂燃烧速度是描述与计算其燃烧特性的重要参数。由于底排药剂为机械混合物，微观结构不均匀且具有多相性，实际燃烧是十分复杂的过程，目前还没有比较完整的燃烧物理模型［1］。通常为便于分析问题，假定底排药剂成分和物理化学性能均匀一致，且可视为按平行层规律燃烧，服从几何燃烧定律，并采用指数燃烧模型描述其燃烧速度。

文献［4］中通过将某底排药柱切割并打磨形成20 mm×10 mm ×3 mm 细条状试验样品，对装填密度分别为Δb1=160 kg/m3与Δb2=100 kg/m3进行了密闭爆发器实验，结果如图1所示。

试验表明，两种装填密度对应的最大压力分别为pb1=173.57 MPa 与pb2=98.3 MPa。基于底排药柱平行层燃烧定律，采用文献［5］中计算发射药火药力fb和余容αb的方法(不考虑热散失的修正)，

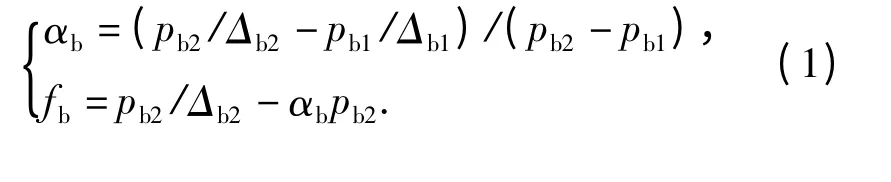
图1 平均压力—时间曲线Fig.1 Average pressure-time curves

计算得fb=850 040 J/kg，αb=0.001 4 m3/kg.

为了拟合燃速模型，取装填密度为160 kg/m3时26 个点的压力—时间数据作为符合数据，设目标函数:

式中:pti为试验压力值;pci为符合计算压力值;n=26.

建立理想状态下的底排药剂密闭爆发器定容燃烧数学模型如(3)式。

式中:zb为底排药剂试样相对燃烧厚度;ab为燃速系数(m/(s·Panb));nb为燃速压力指数;eb为试样一半厚度(m);ψb为燃烧百分比;χb、λb与μb为形状特征量;ρb为底排药剂密度(kg/m3).

通过求解(3)式，采用Hook-Jeeves 模式搜索最优化方法［6］，得到最优的燃速系数与压力指数分别为ab=8.510 ×10-8m/(s·Panb)和nb=0.579.计算与试验结果符合的情况如图2所示。

文献［4］采用最小二乘法的燃速拟合方法［5］得到的结果是:ab=1.251 ×10-8m/(s·Panb)，nb=0.567.通过对比不难发现，本文的计算结果与试验值的符合程度要更好一些，特别是当压力p ＞40 MPa的情况。故高压工况下底排药剂燃速模型可采用下式:

式中e 为药剂烧掉厚度(m).

图2 试验值与计算值的符合情况Fig.2 The fitness between experimental and calculated data

2 膛内底排装置燃烧模型

2.1 物理模型

火炮膛内底排装置内底排药剂燃烧示意图及底排药柱结构图分别如图3和图4所示。

图3 火炮膛内底排装置Fig.3 The base bleed unit in gun bore

图4 底排药柱结构Fig.4 The structure of base bleed propellant

为便于建立膛内底排装置内底排药柱燃烧数学模型，提出如下基本假设:1)底排药柱燃气的温度保持常量，且其化学组分与热力学特性保持不变，忽略火炮装药燃气温度的影响;2)将底排药柱燃气视为理想气体，满足理想气体方程，不考虑凝聚相的影响;3)燃气在底排装置出口的流动为一维等熵定常流;4)底排药柱燃烧服从平行层燃烧规律和指数燃烧定律;5)弹丸膛内运动过程加速旋转，导致底排药柱侧面因受压变形，狭缝结合紧密，不发生燃烧，而仅考虑底排药柱弧面燃烧及旋转对燃速的影响;6)忽略烧蚀性对底排药柱表面燃烧的影响。

2.2 数学模型

基于上述基本假设，建立了膛内底排装置内药柱燃烧的数学模型，如(5)式所示。

当dm/dt ＞0 时，表示燃气流出底排装置;当dm/dt ＜0时，表示燃气流入底排装置。式中:xs=pbSe/为背压，取弹底压力pd(Pa)，pb为底排装置内压力(Pa);x'b=pb/pe;t 为时间(s);R 为气体常数，取R=401.1 J/(kg·K);Tb为药剂燃气绝热温度，Tb=1 812 K;Tg为弹底发射药燃气温度;S 为药柱弧面燃烧面积(m2);为弧面燃速(m/s);ρp为底排药柱密度(kg/m3);ρg为燃气密度(kg/m3);为喷口质量流率(kg/s);V 为燃烧室容积(m3);Se为底排装置喷口面积(m2);r 为药柱内半径(m);L 为药柱长度(m);ε'为旋转修正系数;k为绝热指数，考虑到膛内发射药燃气流进或流出底排装置占主导因素，这里取k=1.25.

对于ε'，采用某低阻底排弹旋转修正因子［1，7］附加符合修正因子的方法，即

式中:α 为燃速符合修正因子，取α=0.986;ε 满足(7)式的形式。

3 火炮—底排弹内弹道零维数学模型

根据文献［8］提出如下基本假设:1)忽略底排药柱受膛内装药燃气热点火过程，认为经过某一延迟时间tc，药柱瞬间达到全面着火燃烧;2)考虑底排药剂燃烧及发射药燃气涌入底排装置空腔对弹后空间参数变化的影响;3)不考虑火炮身管热散失;4)用一个拉格朗日问题的特殊解联系平均压力与弹底压力的关系，依此求取弹底燃气温度;5)考虑底排药剂燃烧对弹质量改变的影响。

基于上述基本假设，建立了单一主装药火炮发射底排弹的内弹道零维模型，如(8)式所示。

式中:ac为火炮主装药燃速系数(m/(s·Pan));nc为主装药燃速压力指数;pd为弹底压力(Pa);f'为等效火药力(J/kg);mtot为底排弹初始全弹质量(kg);tc为底排药柱全面燃烧时刻(s);φ1为次要功系数。其它参数含义见文献［8］。

4 数值计算

针对某155 mm 火炮和所配备的底排弹，基于(4)式～(8)式所建立的底排装置燃烧数学模型及与火炮内弹道耦合数学模型，编制仿真程序，计算分析底排装置膛内的燃烧特性。

4.1 基本参数

4.1.1 火炮及弹丸参数

药室容积W=0.024 m3，身管长度lg=7.37 m，身管横截面积S=0.195 6 m2，火炮缠度20;弹径d=0.15 m，全弹质量(含底排装置)mtot=48 kg，次要功系数φ1=1.08，启动压力p0=30 MPa，弹丸初速v0=900 m/s.

4.1.2 底排装置参数

药柱质量mb=1.08 kg，药柱外径do=120 mm，药柱内径di=43 mm，药柱长度76 mm，狭缝数量n=3，狭缝宽度2c=3 mm，初始空腔容积9.55 ×10-5m3;药剂密度ρb=1.37 ×103kg/m3，药剂爆温Tb=1 812 K，火药力fb=850 040 J/kg，余容αb=0.001 4 m3/kg，喷口直径44.5 mm;燃气比热比1.283;燃速系数ab=8.510 ×10-8m/(s·Panb)，燃速压力指数nb=0.579.

4.1.3 火炮符合装药参数

药型12/7 单基药，装药量ω=15 kg，密度ρ=1 600 kg/m3;火药力fb=990 000 J/kg;余容αb=0.001 m3/kg，发射药爆温Tg0=2 400 K，燃气比热比1.25;燃速系数ac=1.688 ×10-8m/(s·Panc);燃速压力指数nc=0.828.

4.2 计算分析

基本假设:1)不考虑点火药压力的影响;2)底排装置破膜时，空腔内瞬时达到与喷口外部相同的压力(弹底压力)，且底排药剂全面燃烧;3)底排装置内燃气温度恒定，取发射药燃气爆温;4)忽略底排装置内燃气质量对弹丸质量改变的影响，仅考虑底排药剂燃烧掉的质量。

当tc=0 时，即主装药与底排药柱同时全面着火燃烧。对弹丸初速v0=900 m/s，最大平均压力pmax=320 MPa 进行符合计算，得到底排药柱燃烧掉的药剂质量Δmb=8.22 g.设Δp=pb-pd，即底排装置内平均压力与弹底压力的差，计算得到弹底压力pd与压差Δp 随时间t 变化情况，如图5所示;流经底排装置喷口处的燃气质量m 及质量流率dm/dt随时间t 的变化情况，如图6所示。

由图5和图6可以看出:1)随着膛内压力的逐渐升高，底排装置内外压差的不断加大，发射药燃气不断涌入底排装置内。当t≈7.5 ms 时，底排装置内外压差达到最大值，Δp 约为40 000 Pa;当t≈8.5 ms时，燃气质量流率达到最大值，约为6 000 g/s;2)随着底排药剂的燃烧不断加剧，底排装置内外压差逐渐减小，在膛内最大压力附近，内外压差基本趋于振荡平衡，持续时间约3 ms;3)当t≈13 ms 时，过了膛内最大压力点附近，平衡态被打破，底排装置内燃气开始流向弹底区域，压差从大到小并再次趋于平衡。4)底排弹在膛内的整个过程中，流入装置的燃气与流出的基本平衡，底排药剂的燃烧几乎全部用来建立装置空腔的压力。

图5 pd-t 与Δp-t 曲线Fig.5 pd-t and Δp-t curves

图6 m-t 和-t 曲线Fig.6 m-t and -t curves

计算了不同底排药柱全面着火燃烧延迟时间tc对弹丸初速v0及药柱燃烧量Δm 的影响如图7所示。通常情况下，底排药剂燃速系数与燃速压力指数在不同压力下是不一样的，这里为了便于分析，仅考虑燃速压力指数nb不同对底排药柱燃烧量Δm的影响，计算结果如图8所示。

由图7可以看出，底排药剂点火全面燃烧延迟时间tc对弹丸初速v0影响不大，且呈波动变化，相对于基准计算情况，最大不超过0.4 m/s;底排药剂燃烧量Δm 随tc的增大而大致呈指数递减趋势，从量值上看，认为计算值要比实际值小，主要是由于没有考虑燃速系数与燃速压力指数随压力变化的影响。由图8不难发现，燃速压力指数nb变化对Δm 有较大影响，因此，符合计算出的底排药剂燃烧量Δm=8.22 g 偏小，但不影响定性分析。

图7 v0 与Δm 受tc 的影响Fig.7 v0 and Δm affected by tc

图8 不同的nb 引起的Δm 变化情况Fig.8 The change of Δm caused by various nb

5 结论

采用优化方法符合计算出的高压工况底排药剂燃速模型优于传统最小二乘法的拟合结果;从计算结果的情况看，所建立的膛内底排装置燃速模型与火炮—底排弹零维内弹道模型是适用的。通过数值计算得出:1)膛内底排装置压力变化的基本趋势和喷口流量的变化规律;2)膛内过程底排药剂燃烧量约为8.22 g;3)由于延迟时间tc引起的初速v0变化量不大，最大不超过0.4 m/s，故可忽略不计;4)随着延迟时间tc的增加，引起的底排药剂燃烧量Δm 改变基本呈指数递减趋势。研究结果对于定性与定量分析膛内底排装置的燃烧特性和射击诸元有工程参考价值。

References)

［1］ 郭锡福.底部排气弹外弹道学［M］.北京:国防工业出版社，1995.GUO Xi-fu.Exterior ballistics of base bleed projectile［M］.Beijing:National Defense Industry Press，1995.(in Chinese)

［2］ James E Danberg.Analysis ofthe flight performance of the 155 mm M864 base burn projectile，AD-A222-624［R］.US:DTIC，1990.

［3］ Lyle D Kayser，John D Kuzan，David N Vazguez.Flight testing for a 155 mm base burn projectile，AD-A222-562［N］.US:DTIC，1990.

［4］ 陆春义.底排装置强非稳态燃烧特性研究［D］.南京:南京理工大学，2009.LU Chun-yi.Study on characteristics of unstable combustion of base bleed unit［D］.Nanjing:Nanjing University of Science and Technology，2009.(in Chinese)

［5］ 官汉章，邹瑞荣.实验内弹道学［M］.北京:兵器工业出版社，1997.GUAN Han-zhang，ZOU Rui-rong.Experimental interior ballistics［M］.Beijing:The Publishing House of Ordnance Industry，1997.(in Chinese)

［6］ 薛毅.最优化原理和方法［M］.北京:北京工业大学出版社，2001.XUE Yi.Principles and methods of optimization［M］.Beijing:Beijing University of Technology Press，2001.(in Chinese)

［7］ 张领科，周彦煌，余永刚.底排装置工作不一致性对射程散布影响的研究［J］.兵工学报，2010，31(4):442-445.ZHANG Ling-ke，ZHOU Yan-huang，YU Yong-gang.Research on range dispersion of base bleed projectile caused by inconsistent working characteristics of base bleed unit［J］.Acta Armamentarii，2010，31(4):442-445.(in Chinese)

［8］ 金志明，袁亚雄，宋明.现代内弹道学［M］.北京:北京理工大学出版社，1992.JIN Zhi-ming，YUAN Ya-xiong，SONG Ming.Modern interior ballistics［M］.Beijing:Beijing Institute of Technology Press，1992.(in Chinese)