膛口装置三维流场的数值模拟及制退效率计算

张焕好，陈志华，姜孝海，韩珺礼

(南京理工大学 瞬态物理国家重点实验室，江苏 南京210094)

0 引言

弹丸发射出膛口瞬间，身管内高温、高压火药燃气在膛口急剧膨胀，形成以欠膨胀射流为主的瞬态膛口流场［1］。膛口中流出的高温、高压、高速气流对炮身所产生的反作用力，使炮身后坐增大，并对弹丸飞行产生初始扰动，影响射击精度。

为了改善武器系统后坐性能，可在大威力炮(枪)膛口上加装膛口制退器，使流出的高温高压火药燃气在制退器内膨胀，将内能转变为动能，并使部分火药燃气从制退器侧孔排出，提供与后坐方向相反的作用力，达到减少后坐能量的目的［2-3］。然而，加装膛口制退器后会增大炮手区域的冲击波峰值，一般对炮手危害程度随制退效率的提高而增大。因此，为了提高膛口制退器效率，减弱或消除其副效应，需对制退器内外流场进行研究，完善膛口制退器设计理论。

目前，由于受测试方法限制，通过高速摄影技术捕捉膛口外流场，却无法对制退器内流场进行显示。近年来，国内外学者开始应用计算流体力学对膛口流场与制退器效率进行计算与研究。如Sakamoto等［4］利用MUSCL 格式计算了三维膛口流场。Aibarov 等［5］则对三维带化学反应的膛口流场进行了数值模拟。Cler 等［6］分别采用Fluent 6.1 中2 阶无粘求解器和基于Galerkin 方法的DGM 代码以及非结构化网格对不考虑运动弹丸的膛口流场(G3 步枪发射7.62 mm 北约制式枪弹)进行了数值模拟，并与试验阴影对照，结果表明初始流场与试验阴影相符，但火药燃气流场并不太吻合。随后，Bin 等［7］基于轴对称Euler 方程的DRP 格式及结构化网格对膛口(G3 步枪发射7.62 mm 北约制式枪弹)流场进行了模拟，所得初始流场及火药燃气流场均与试验阴影相吻。乐贵高等［8］利用Osher 格式及非结构网格对某火炮膛口气流场进行了三维求解。姜孝海等［1，9］基于ALE 方程的结构化动网格和嵌入网格法以及Roe 格式对弹丸由膛内高压气体推动射出到完全飞离初始流场的整个过程进行了数值模拟，并讨论了初始流场、火药燃气流场的形成与发展以及与弹丸相互作用的过程。

关于制退器流场的模拟则相对较少。Yang等［10］利用迎风格式及结构化动网格技术对弹丸飞离炮双挡板制退器过程中二维膛口流场进行了数值模拟，并与试验测得超压峰值及超压稳定值进行对比。张辉等［3］采用三维任意坐标系下Euler 方程对某口径火炮带3 排侧孔制退器的膛口流场进行了数值模拟，并提供有关膛口流场的数据。江坤等［11］采用无粘模型及非结构化网格对装有炮口3 排侧孔制退器车载炮膛口冲击波场进行了数值模拟，并对制退器效率进行估算。

膛口流场包含高速运动弹丸、射流、冲击波、湍流与燃烧及爆轰等相互作用，另外，由于高温、高压火药燃气的急剧膨胀以及与制退器内壁面的激烈碰撞，使制退器内流场结构同样具有复杂高瞬态特点。因此，膛口内、外流场以及制退器效率的准确计算，对数值模拟要求很高，首先数值格式需准确捕捉弹丸发射过程中激波，另外还要对弹丸运动以及二次爆燃等进行计算与描述，虽然非结构化网格在此方面有优点，但因耗散过大，会使格式计算精度下降。基于此，本文采用三维非定常Euler 方程，结合能准确捕捉激波的高精度Roe 格式和结构化动网格技术，对弹丸飞离开腔式膛口制退器过程中，制退器内与膛口流场结构的变化过程进行数值模拟。同时根据数值结果对制退器的计算效率进行计算，并与文献［12］的试验结果进行对比。

1 数值方法及计算模型

1.1 控制方程

采用三维非定常Euler 方程

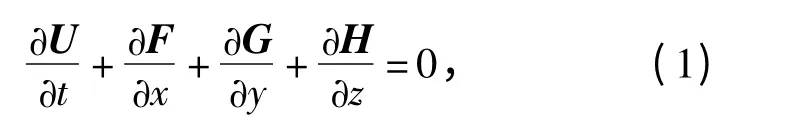
式中:U=［ρ，ρu，ρv，ρw，E］T;F=［ρu，ρu2+p，ρuv，ρuw，(E+ p)u］T;G=［ρv，ρuv，ρv2+ p，ρvw，(E+p)v］T;H=［ρw，ρuw，ρvw，ρw2+p，(E+p)w］T.其中:ρ 为气体密度;u、v、w 分别为x、y 和z 方向的速度分量;E 为总能量，其表达式为

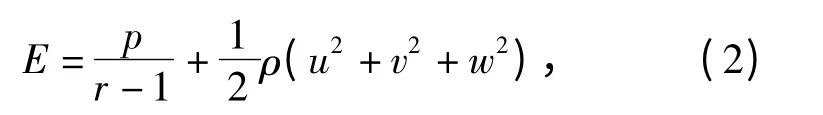
式中r 为理想气体绝热指数。理想气体的状态方程为

式中R 为通用气体常数。方程(1)式～(3)式组成封闭方程组。

1.2 数学方法及验证

采用有限体积法对方程进行离散。时间推进采用2 阶精度Runge-Kutta 法，对流项则用Roe 格式离散为

式中:ARoe，j+1/2为Roe 矩阵;为Roe 通量。

为了检验本文算法对膛口流场复杂波系的捕捉能力，取7.62 mm JS 狙击步枪膛口流场为算例。图1为t=0.43 ms 时，初始膛口流场的计算阴影(上)与压力(下)等值线和文献［12］的试验阴影的对比图。由图1可见，计算结果能成功捕捉膛口流场中瓶状激波等典型射流结构，并与试验结果吻合。

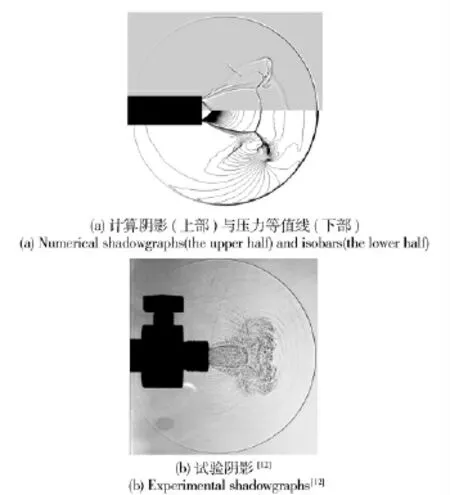
图1 计算结果与试验结果对比Fig.1 Comparison of calculated and experimental results

1.3 计算模型及动网格方法

带开腔式膛口制退器的37 mm 火炮计算模型与计算域网格分布如图2所示。初始时，弹丸底部到炮膛端部距离为2 300 mm，外流场计算域取半径为85 mm、高为384 mm 的圆柱体。为了减少网格带来的格式耗散，将整个计算域划分为96 万个6 面体结构化网格系统。而计算膛口制退器效率则采用200 万个6 面体结构化网格。

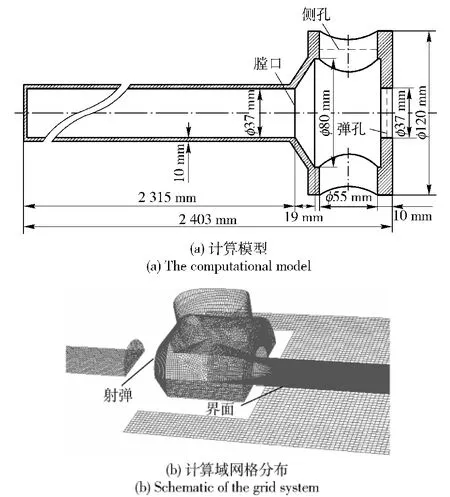
图2 带膛口制退器的火炮结构示意图Fig.2 Schematic diagram of cannon with muzzle brake

为了模拟弹丸相对炮管的运动过程，把整个计算域划分为静网格区和动网格区，如图2(b)中弹丸前后区域为动网格，而运动分界面将动静网格区分开。计算过程中，弹丸以867 m/s 的恒定速度沿x轴飞离膛口制退器，弹丸前后的动网格相对于静网格滑动，其前端网格被不断合并，而后端则不断生成新网格，以弥补弹丸运动造成的尾部空白。

计算所需的初始条件如弹底身管内的初始压力、速度与火药燃气温度等根据内弹道计算得到，其结果如图3所示，膛口外流场为常温常压大气条件。

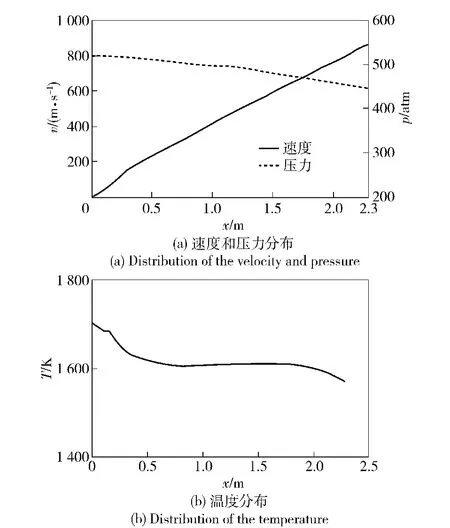
图3 弹丸离开膛口瞬间的膛内燃气速度和压力及温度分布Fig.3 The velocity，pressure and temperature distribution of the combustion gas inside the barrel at the moment of the projectile ejecting from the muzzle

2 结果与讨论

2.1 流场分析

图4为火炮发射时，膛口及开腔式膛口制退器的初始流场计算纹影与试验阴影对比图［12］。此时，弹丸仍在膛内，受其底部高压气推挤在管内加速运动，同时压缩弹头空气，使其在弹丸离开膛口前以欠膨胀射流喷出制退器与炮管膛口，形成初始射流。计算结果清晰地捕捉到初始流场的发展过程，其中各出口射流边界、马赫盘、入射激波、反射激波等所组成的复杂瓶状激波系清晰可见(见图4(a))，并跟试验结果(见图4(b))相符。

图4 流场结构计算结果与试验结果对比Fig.4 Comparison of calculated and experimental results

当火药燃气喷出炮口后，由于制退器分流作用，在制退器内形成十分复杂的流场结构。图5为本文计算条件下，开腔式膛口制退器内压力和密度等值线随时间的变化图，其中每幅图上、下各半分别为压力和密度。可知，弹丸飞离膛口后，其底部高温、高压火药燃气紧随其流出膛口，在制退器内迅速膨胀，并与制退器内壁面及弹丸底部相互作用与反射(见图5(a)).随着制退器内壁面上、下两道反射激波在轴线上的相互碰撞以及它们与膛口高压燃气的相互作用，最终在制退器内部耦合成一道强激波(见图5(b))，提高当地压力及密度，造成膛内气流短暂拥塞。由于膛口高速膨胀火药燃气与制退器内部反射流场的相互作用，使激波形状发生变化，随着制退器反射激波的减弱，膛口高压燃气流逐渐呈现强势，在制退器内高压膨胀使激波变形，并在制退器壁面与强激波间形成二次激波(见图5(c)).随后，膛口高压燃气流占据统治地位，推动激波在制退器轴向出口内形成三维斜激波(见图5(c)～图5(e))，同时，二次激波(见图5(d))因膨胀占优而消散(见图5(e)).最终在制退器内部及膛口形成复杂波系结构(见图5(f))，并在持续短暂时间后，最终消失。

图6则为t=0.2 ms 时，膛口制退器内的截面速度矢量图。在xOy 平面上，由于制退器侧孔分流作用，部分气流加速向侧孔排出，然而因初期受制退器内壁面反射气流的影响，在制退器内形成明显的速度分界面(见图6(a)).而从y=43 mm 的xOz 平面速度矢量图可见，前壁面上气流除了向轴向反射外，还有部分气流沿着侧孔内壁面发生旋转(见图6(b))，因此在xOz 面上形成复杂涡结构。此外，与膛口高速膨胀气流的碰撞则形成明显的速度分界层。由此可知，高温、高压火药燃气在制退器三维空间内的膨胀加速、碰撞、反射以及旋转使膛内流场结构具有三维复杂特征。

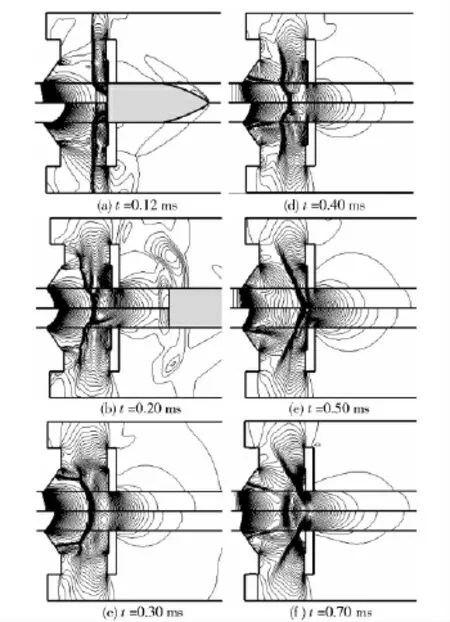
图5 压力(上部)和密度(下部)等值线分布图Fig.5 Distributions of the isobars (the upper half)and the isopycnics (the lower half)

图7为不同时刻膛口制退器x 轴上压力分布曲线。图8为相应时刻膛口制退器y 轴上压力分布。可知，高温、高压火药燃气流出膛口后，在制退器内急剧膨胀，迅速提高出口附近的气流速度(见图7膛口)。随后，前导激波与膛口制退器内壁面相碰撞，提高当地压力(见图7，t 为0.2～0.4 ms)形成出口通道阻塞，使弹孔出口(见图7弹孔)附近气流速度急剧下降，因而在0.2～0.6 ms 期间，压力在x 轴上的分布呈现出较为明显的突变特性。同时，由于受激波在制退器内的来回反射影响，火药燃气流在y 轴上的压力分布出现间断，且曲线形状随时间的变化剧烈(见图8).可见，在火药燃气流出初期，制退器y轴上具有高度时空瞬态特性。然而，随着气流持续流出，弹孔进口(见图7弹孔，t=0.7 ms)处的拥塞状况逐渐得到缓解，1 ms 以后，气流压力x 轴及y 轴上的分布趋势变化呈相对较缓降低趋势。

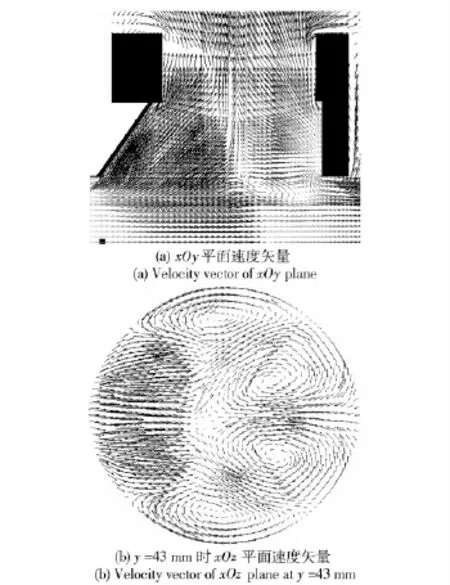
图6 t=0.2 ms 时开腔式膛口制退器内速度矢量图Fig.6 Velocity vector in muzzle brake at t=0.2 ms

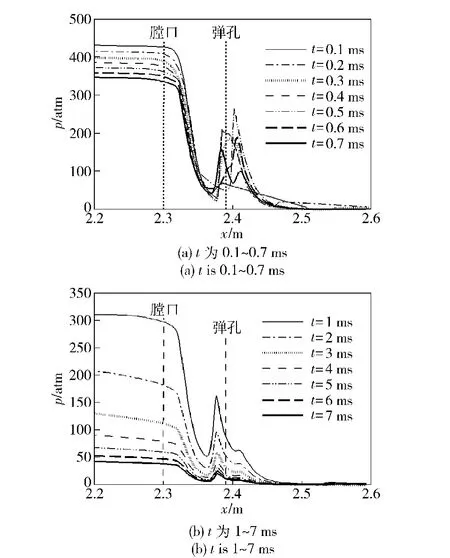
图7 不同时刻膛口制退器在x 轴上的压力分布曲线Fig.7 Pressure distributions along x axis of muzzle brake at different time

表1为不同时刻，开腔式膛口制退器中3 孔内的流场参数计算值，其中，各参数均为各孔的面积平均值。初始时刻，火药燃气流均以超音速(马赫数＞1)流经3 孔。对3 孔上质量流量m·进行统计发现流进膛口的质量流量等于弹孔和侧孔流出质量流量之和，满足质量守恒定律。由于强激波以及二次激波在膛口附近的影响，使得膛口出口压力及密度在0.4 ms 时突然上升并随后下降。在0.2～0.5 ms间，气流拥塞在弹孔出口处，降低了弹孔的出口速度同时提高了该处压力及密度，随后均持续下降。同时，由表可知，t=1 ms 以前，3 孔出口气流速度方向均与出口平面呈一定角度，并且随着时间发生剧烈变化。t=1 ms 后，气流逐渐趋向于90°垂直于孔平面喷出。基于以上分析说明火药燃气喷出炮口初期，在膛口制退器内形成具有时空瞬态特性的三维燃气流场。

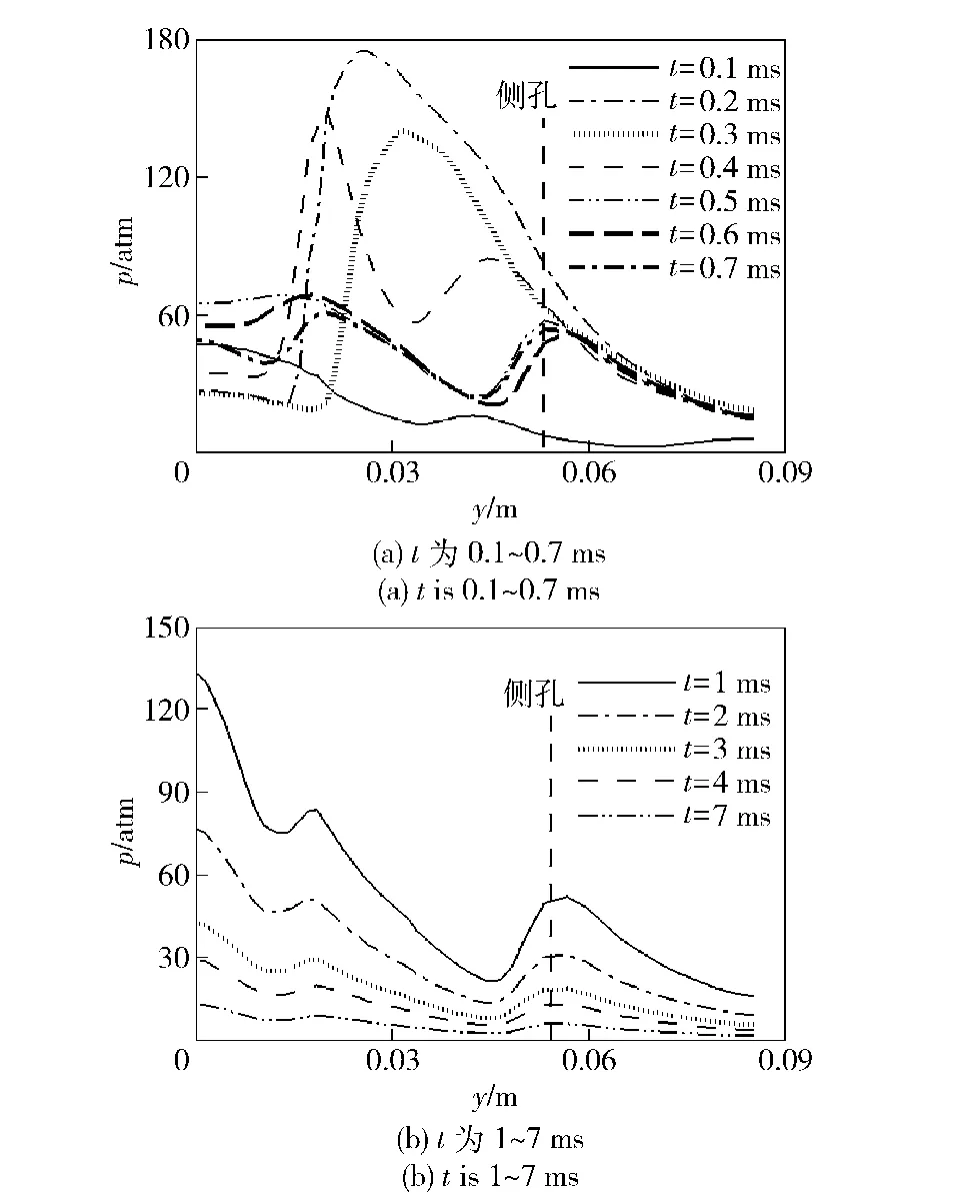
图8 不同时刻膛口制退器在y 轴上的压力分布曲线Fig.8 Pressure distributions along y axis of muzzle brake at different time

2.2 制退效率计算

取37 mm 火炮弹丸质量mb=0.764 7 kg，装药量ω=0.221 kg，弹丸出炮口初速v0=867 m/s.图9为火炮膛底、制退器以及合力随时间变化的数值计算分布曲线。图10为火炮膛底冲量Io以及总冲量In随时间变化的数值计算分布曲线。可知，加入开腔式膛口制退器后，由于部分火药燃气通过制退器侧孔流出，提供了与膛底方向相反的作用力，从而降低了炮身的合力。由图10可知，加装制退器后降低了后坐总冲量，从而改善了火炮的后坐性能。当身管内气体基本排空时(管内压力降到2 atm 左右)，火药气体作用在身管上的冲量为I0=-169.3 N·s，而带开腔式膛口制退器后作用在身管上的总冲量则为In=5.75 N·s.定义炮口装置火药气体作用系数:

表1 开腔式膛口制退器3 孔的流场参数Tab.1 The flow field parameters of the three-way muzzle brake

无炮口制退器的火药气体作用系数:

制退器效率:

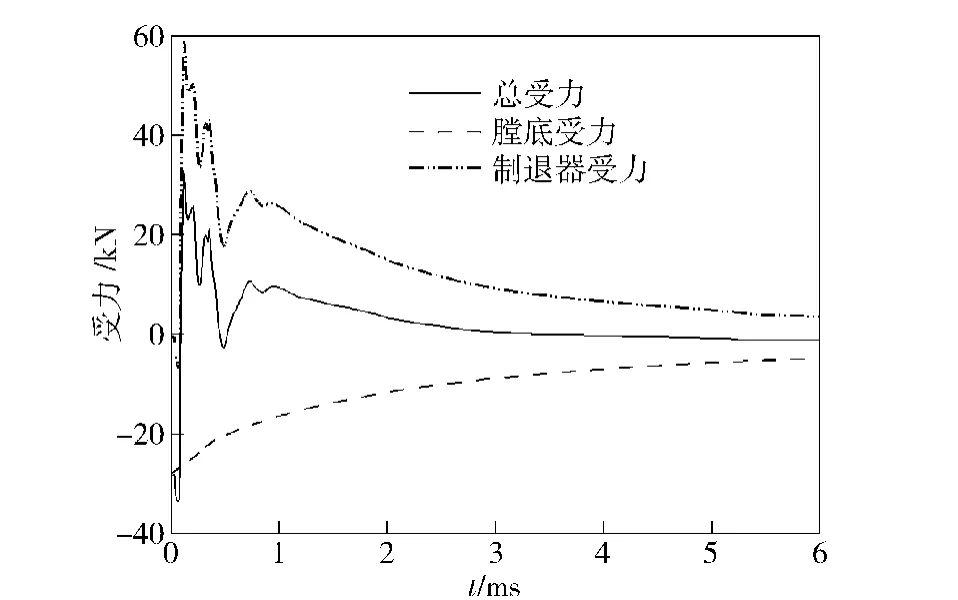
图9 火炮膛底和制退器及总受力曲线Fig.9 The curves of chamber bottom force，muzzle brake force and total thrust

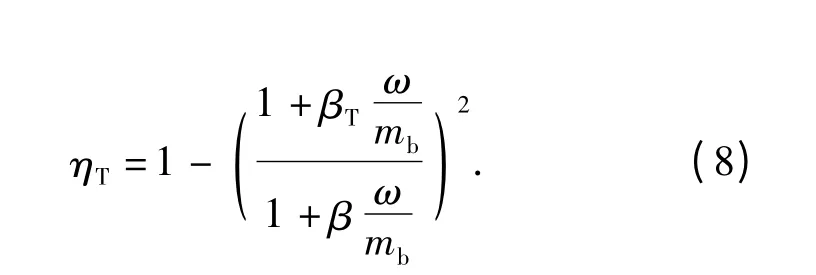
此时，计算所得开腔式制退器效率为ηT=34.12%，而文献［12］自由后坐台相关试验结果约为33%左右，计算结果基本与试验结果相符合。

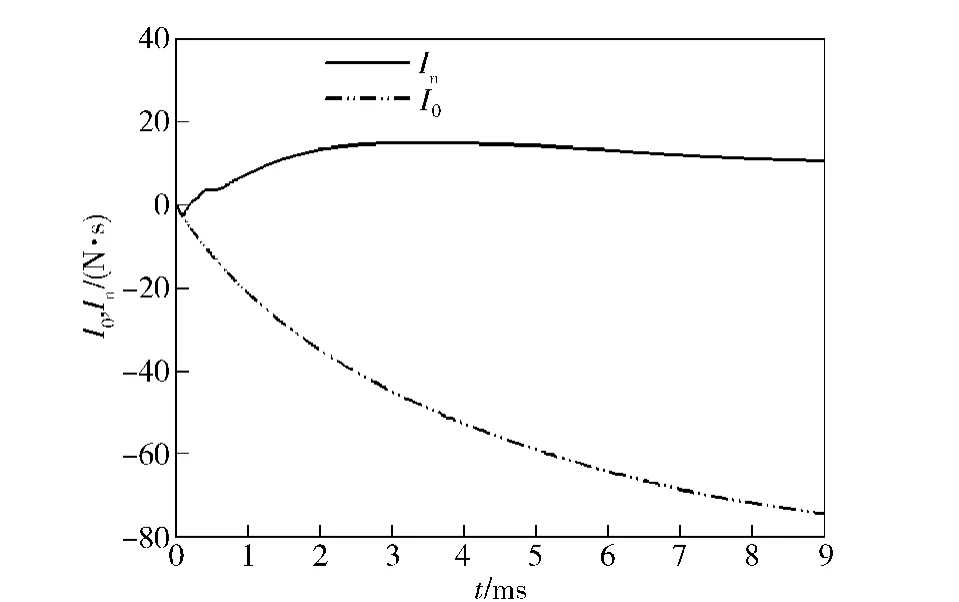
图10 火炮膛底冲量I0及总冲量In曲线Fig.10 Distribution of chamber bottom impulse I0 and total impulse In

3 结论

基于三维Euler 方程，结合高精度Roe 格式与结构化动网格技术，对膛口加装开腔式制退器的弹丸发射与运动过程进行了数值模拟。计算结果表明，虽然膛口加装了制退器，其膛口流场典型特征不变，但因火药燃气在制退器内高速膨胀，并与制退器内壁面及弹丸相互作用，在膛内形成复杂波系结构，且具有时空瞬态特性。另外，由于制退器分流作用，部分气体由侧孔排出，从而降低后坐总冲量。基于数值计算结果，所得开腔式制退器制退效率为34.12%.计算流场结构与制退效率都与文献［12］试验结果相吻，可为未来类似研究提供重要参考。

致谢本文研究与撰写过程中得到了李鸿志院士的悉心指导与支持，在此表示感谢。

References)

［1］ 姜孝海，李鸿志，范宝春，等.基于ALE 方程及嵌入网格法的膛口流场数值模拟［J］.兵工学报，2007，28(12):1512-1515.JIANG Xiao-hai，LI Hong-zhi，FAN Bao-chun，et al.Numerical simulation of muzzle flow field based on ALE equation and chimera grids［J］.Acta Armamentarii，2007，28(12):1512-1515.(in Chinese)

［2］ 张月林.火炮反后坐装置设计［M］.北京:国防工业出版社，1984:2-55.ZHANG Yue-lin.Design of the reverse recoil device of the cannon［M］.Beijing:National Defense Industry Press，1984:2-55.(in Chinese)

［3］ 张辉，谭俊杰，崔东明.带制退器膛口流场的三维数值模拟［J］.力学与实践，2008，30(4):30-34.ZHANG Hui，TAN Jun-jie，CUI Dong-ming.Numerical simulation of 3D muzzle brake flow field［J］.Mechanics and Practice，2008，30(4):30-34.(in Chinese)

［4］ Sakamoto K，Matsunnaga K，Fukushima J，et al.Numerical analysis of the propagating blast wave in a firing range［C］//19th International Symposium In Ballistics.Interlaken，Switzerland:IBC，2001:289-296.

［5］ Aibarow A V，Babayev D B，Mironov A A.Numerical simulation of 3D muzzle brake and missile launcher flow field in the presence of movable objects［C］//20th International Symposium In Ballistics.Orlando:IBC，2002:225-232.

［6］ Cler D L，Chevaugeon N，Shephard M S，et al.CFD application to gun muzzle blast a validation case study，AIAA-2003-1142［R］.Reno，Nevada:AIAA，2003.

［7］ Bin J H，Kim M W，Lee S.A numerical study on the generation of impulsive noise by complex flows discharging from a muzzle［J］.Int J Numer Meth Engng，2008，75:964-991.

［8］ 乐贵高，马大为，冯勇，等.某火炮膛口流场数值仿真［J］.兵工学报，2004，25(1):19-22.LE Gui-gao，MA Da-wei，FENG Yong，et al.Numerical simulation of muzzle blast flow fields of large caliber guns［J］.Acta Armamentarii，2004，25(1):19-22.(in Chinese)

［9］ Jiang X H，Chen Z H，Fan B C，et al.Numerical simulation of blast flow fields induced by a high-speed projectile［J］.Shock Waves，2008，18:205-212.

［10］ Yang G，Causon D M，Ingram D M.Calculation of compressible flows about complex moving geometries using a three-dimensional Cartesian cut cell method［J］.Int J Numer Meth Fluids，2000，33:1121-1151.

［11］ 江坤，钱林方.某火炮炮口制退器性能的研究［J］.弹道学报，2006，18(3):55-57.JIANG Kun，QIAN Lin-fang.A study on the muzzle brake performance of guns［J］.Journal of Ballistics，2006，18(3):55-57.(in Chinese)

［12］ 李鸿志，姜孝海.弹道实验图集［R］.南京:瞬态物理国家重点实验室，2009.LI Hong-zhi，JIANG Xiao-hai.The album of experimental ballistics［R］.Nanjing:National Key Laboratory of Transient Physics，2009.(in Chinese)