基于信息量等值的火工品可靠性评估小样本方法

董海平，赵霞，蔡瑞娇

(北京理工大学 爆炸科学与技术国家重点实验室，北京100081)

0 引言

随着武器装备和航空航天器技术的发展，对与之配套的火工品可靠性(本文指发火可靠性)要求越来越高，大部分火工品的可靠度指标已达到了0.999，有的甚至达到了0.999 5.若采用经典方法［1］评估其可靠性，因所需样本量大，工程中常常难以实施。为了解决火工品高可靠性的评估问题，田玉斌［2］提出了计量与计数法相结合的Bayes 可靠性评定方法，在很大程度上减少了样本量;冯蕴雯等［3］、张士峰等［4］对小子样Bayes 可靠性评定方法进行了改进，使样本量进一步减少［3-4］。刘炳章等［5］、刘杰等［6］提出基于熵强化系数，选择熵强化系数等于功能裕度系数的点进行试验，能使试验熵最大，试验所需样本量最小，即“最大熵试验法”，初步解决了航天火工品高可靠性的评估问题;荣吉利等［7］利用裕度思想提出了一种加严条件下的火工机构的可靠性评估方法。这些方法对火工品高可靠性小样本评估起到了很好的推动作用。

可靠性试验的目的是获取产品的可靠性信息，以此对产品可靠性进行评估［8］，因此，可靠性评估技术的关键是获取足够多的可靠性信息量。信息论中，信息量是随机变量不确定性的度量。在火工品可靠性试验中，其试验结果是随机的，外界施加的能量越高，发火可靠度越高，其试验结果不确定性就越小，从试验成功中获得的可靠性信息量就越少。按经典方法评估时，一般直接在技术指标规定的工作刺激量处进行试验，由于在工作刺激量处的发火可靠度高，因此在该处进行的每发产品试验成功获得的可靠性信息量就少，为获得足够的可靠性信息量需要样本量就大;反之，如果能在低刺激量处进行试验，每发产品试验成功获得的可靠性信息量就多，为获得同样的可靠性信息量需要样本量就可以小一些。本文根据在低刺激量下试验比在高刺激量下试验成功能获得更多可靠性信息量的原理，降低试验刺激量，使在低刺激量处少量样本的试验获得的可靠性信息量与根据GJB 376—1987 评估时在工作刺激量处进行大量试验获得的可靠性信息量等值，实现小样本方法与采用GJB376—1987 方法评估结果等效。

1 火工品可靠性试验信息量等值评估原理

信息论中，一个随机事件所含有的信息量称为自信息量，定义［9］为

式中:P 为随机事件发生的概率;I 代表两种含义:当随机事件发生以前，表示事件的不确定性;当随机事件发生以后，表示该事件所含有(或所提供)的信息量。

信息量采用的单位取决于对数所选取的底，如果采用以e 为底的自然对数，则所得的信息量单位为奈特(nat，nature unit 的缩写)，即I=-lnP.

火工品可靠性试验属一次性作用产品的成败型试验，每次试验成功获得的可靠性信息量可以采用类似的方式来度量，即可定义为

式中:R 为可靠度，即火工品试验的发火概率;TI 表示每发产品发火后所提供的可靠性信息量。

火工品的可靠性指标一般表示为:对于工作刺激量xH，在置信水平γ 的情况下，可靠度不低于R.如果采用GJB376—1987 评估，在无失效的情况下，要试验nxH发产品，其中nxH由(3)式计算。

若火工品感度服从正态分布，则xH处的可靠度为其中μ、σ 为未知的感度分布参数。按照上述火工品可靠性信息量的定义，在xH处单发产品试验成功获得的信息量为TIH=-lnRxH.按照信息量可加性原理，nxH发产品试验全部成功获得的总信息量为nxHTIH=nxH(-lnRxH).

选择某一低刺激量xL进行试验，使xL＜xH，xL处的可靠度为其中μ、σ 为未知的感度分布参数。在xL处单发产品试验成功获得的信息量为TIL=-lnRxL，若在xL处试验nxL发产品，则nxL发产品全部试验成功获得的总信息量为nxLTIL=nxL(-lnRxL).

关于火工品的可靠性评估，一般认为按GJB376—1987 评估试验中包含了足够的可靠性信息量，评估结果可信。因此，令在低刺激量xL处试验nxL发产品获得的可靠性信息量与按GJB376—1987 在工作刺激量xH处试验nxH发产品获得的信息量相等，即

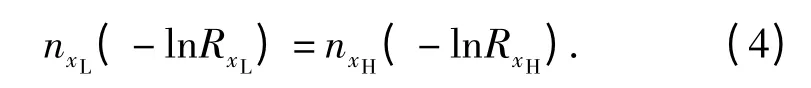
(4)式称为火工品可靠性信息量等值方程。

由于刺激量xL＜xH，则相应的可靠度RxL＜RxH，即(-lnRxL)＞(-lnRxH)，根据等值方程(4)式易得到nxL＜nxH，即降低了样本量。如果xL越小，则所需的nxL也会越少。实际工程中，为了兼顾生产方和使用方的实际情况，可根据产品的批量和工程实际共同协商确定允许试验的产品数量nxL，然后根据感度试验估计出感度分布参数，再利用信息量等值方程和感度分布模型确定出低刺激量xL，最后在xL处进行少量试验，根据该试验结果作出可靠性判定。

本方法就是根据在高刺激量处试验，其获得的信息量值小，而选择低刺激量进行试验，使单个产品试验获得的可靠性信息量增加，从而达到了降低样本量的目的。

2 小样本评估程序

2.1 计算按GJB376—1987 评估所需的样本量nxH

由置信水平γ，可靠度R，按(3)式计算nxH.

2.2 升降法试验

按GJB/Z377A—1994［10］的规定进行3 组升降法试验，每组样本量为50，然后根据极大似然估计原理求出产品感度分布参数μ、σ 的估计。

2.3 刻度参数纠偏

由GJB/Z377A—1994 规定的升降法试验方案得到的试验结果确定感度分布参数时，μ 的估计是无偏的，而σ 的估计是有偏的［11］。这势必影响可靠度估计的准确性，因此纠偏成为本方法的关键问题。文献［12］对升降法试验σ 估计的纠偏问题进行了计算机模拟研究，得出了σ 估计的纠偏系数，本方法采用该文献提出的纠偏系数对σ 估计进行纠偏，得到经过纠偏处理后的3 组升降法参数估计值的平均值为

2.4 低刺激量xL 的确定

本文以正态分布和对数正态分布为例。

2.4.1 正态分布

nxL可由生产方和使用方根据产品设计、工艺、性能、管理等信息确定，也可采用本方法根据研究结果推荐的样本量，见表1.

表1 试验信息量等值评估方法在低刺激量处的试验样本量推荐表Tab.1 Test number for assessment method based on test information measure equivalence

将nxH、和nxL代入可靠性试验信息量等值方程(4)式，求得xL处的可靠度估计值，然后按(6)式计算

2.4.2 对数正态分布

2.5 结果判定

在刺激量xL处，取确定的试验样本量nxL进行试验，若全发火，则可判定产品满足可靠性指标。

3 大、小样本对比验证试验

某撞击火帽可靠性指标为:γ=0.90，R=0.999.发火上限为落高10 cm，落锤388 ±1 g.

3.1 大样本法评估

由于步进法试验数量较大，且其参数估计稳定，因此在实际工程中常把步进法称为大样本方法。大样本方法是根据步进法试验数据估计分布参数，然后求出满足可靠性指标的刺激量上限，若其上限小于该产品的工作刺激量，则可判定产品达到可靠性指标。

对本产品进行了2 800 发的步进法试验，试验数据见表2所示。

表2 步进法试验数据Tab.2 Test data of run-own method

通过χ2检验得到该撞击火帽感度服从对数正态分布，采用极大似然原理估计出其感度分布参数(对数均值为1.57，对数标准差为0.16)，并计算得与可靠性指标对应的刺激量置信上限为^x0.999U=8.02 cm.

由于发火上限落高为10 cm，则可判断该产品达到了可靠性指标。

3.2 采用本小样本方法评估

由可靠性指标γ=0.90，R=0.999，按(3)式计算可得，nxH=2 303 发。

进行3 组升降法试验，受测量精度的限制，升降法试验中刺激量选正态分布等步长进行，原始数据列于表3中。

根据步进法试验结果，该产品感度服从对数正态分布，因此先将各刺激量(落高)利用y=lnx 转换为对数值，然后利用极大似然估计原理求出参数估计值，见表4所示。

利用文献［12］中的正态分布纠偏系数表对标准差进行纠偏，纠偏后的3 组升降法参数估计值的平均值(对数值)为

表3 3 组升降法试验数据Tab.3 Three groups of test data up-and-down method

表4 3 组升降法参数估计结果(对数值)Tab.4 Parameter estimation values (logarithm)of three groups of up-and-down test data

由产品可靠性指标和表1可确定样本量nxL为22 发。xH=10 cm，对xH取对数yH=lnxH=ln10=2.303.把=1.585，=0.164，lnxH，代入(5)式可求得xH处的可靠度估计=0.999 994.然后把nxH=2 303 发，nxL=22 发，=0.999 994 代 入(4)式，求得xL处的可靠度估计值=0.999 372.再按(6)式求得xL的对数值yL=2.11，再根据(7)式，可求得低刺激量xL=8.2 cm.

在8.2 cm 处试验产品22 发，全部发火。判定该产品发火可靠性达到了置信度γ=0.90，可靠度R=0.999 的指标。

评估结果与大样本方法一致，验证了本小样本方法的可行性。采用本小样本方法进行评估时，3 组升降法试验共用了150 发产品，低刺激量处试验用了22 发，总共用了172 发产品，实现了对可靠度指标为0.999 的评估，所需样本量约为采用GJB376—1987 或步进法进行评估时的1/10，大幅度降低了样本量。

4 结论

本文利用在低刺激量处进行试验比在高刺激量处进行试验能获得更多可靠性信息量的原理，选择低刺激量处进行试验，使较少样本试验获得的总可靠性信息量与根据GJB376—1987 在工作刺激量处进行的大量试验所获得的可靠性信息量相等，以此为基础，建立了火工品可靠性评估小样本方法，大幅度降低了样本量。该方法可解决高可靠性指标的火工品可靠性评定中所需样本量大，试验周期长，耗费高的难题。用本方法已在国内20 多个型号火工品与大样本步进法进行了对比试验验证，结果表明本方法正确、可行，可以在火工品高可靠性评估中推广使用。

References)

［1］ GJB376—1987 火工品可靠性评估方法［S］.北京:国防科技工业委员会，1987.GJB376—1987 Assessment method of reliability of initiating devices［S］.Beijing:Commission of Science Technology and Industry for National Defense，1987.(in Chinese)

［2］ 田玉斌.敏感性产品的可靠性评估方法研究［D］.北京:北京理工大学，2000.TIAN Yu-bin.Studies on reliability estimation for sensitivity products［D］.Beijing:Beijing Institute of Technology，2000.(in Chinese)

［3］ 冯蕴雯，冯元生.极小子样高可靠性成败型产品的贝叶斯评估方法研究［J］.机械科学与技术，1999，18(2):198-200.FENG Yun-wen，FENG Yuan-sheng.Study of Bayes’s estimation for product test of extreme small-sample high-reliability safe-or-failure pattern［J］.Mechanicak Science and Technology，1999，18(2):198-200.(in Chinese)

［4］ 张士峰，樊树江，张金槐.成败型产品可靠性的Bayes 评估［J］.兵工学报，2001，22(2):238-240.ZHANG Shi-feng，FAN Shu-jiang，ZHANG Jin-huai.Bayesian assessment for product reliability using pass-fail data［J］.Acta Armamentarii，2001，22(2):238-240.(in Chinese)

［5］ 刘炳章，丁同才.小子样验证高可靠性的可靠性评估方法及其应用［J］.质量与可靠性，2004，(1):19-22.LIU Bing-zhang.DING Tong-cai.Assessment method of high reliability with small samples and its application［J］.Quality and Reliability，2004，(1):19-22.(in Chinese)

［6］ 刘杰，王普，刘炳章.最大熵试验法及其应用［J］.自动化学报，2007，33(11):1226-1228.LIU Jie，WANG Pu，LIU Bing-zhang.Test method with the maximum entropy and its application［J］.Acta Automatica Sinica，2007，33(11):1226-1228.(in Chinese)

［7］ 荣吉利，白美，刘志全.加严条件下火工机构可靠性评估方法［J］.北京理工大学学报，2004，24(2):118-120.RONG Ji-li，BAI Mei，LIU Zhi-quan.Reliability assessment of pyrotechnical devices under rigorous conditions［J］.Transactions of Beijing Institute of Technology，2004，24(2):118-120.(in Chinese)

［8］ 徐维新，秦英孝.可靠性工程［M］.北京:电子工业出版社，1988.XU Wei-xin，QIN Ying-xiao.Reliability engineering［M］.Beijing:Publishing House of Electronics Industry，1988.(in Chinese)

［9］ 傅祖芸.信息论—基础理论与应用［M］.北京:电子工业出版社，2001.FU Zu-yun.Informatics-basic theory and application［M］.Beijing:Publishing House of Electronics Industry，2001.(in Chinese)

［10］ GJB/Z377A—1994 感度试验用数理统计方法［S］.北京:国防科技工业委员会，1995.GJB/Z377A—1994 Sensitivity tests，statistical methods for［S］.Beijing:Commission of Science Technology and Industry for National Defense，1995.(in Chinese)

［11］ 刘宝光.敏感度数据分析与可靠性评定［M］.北京:国防工业出版社，1995.LIU Bao-guang.Sensitivity data analysis and reliability assessment［M］.Beijing:National Defense Industry Press，1995.(in Chinese)

［12］ 董海平，温玉全，蔡瑞娇.升降法试验标准差估计的偏差研究［C］∥中国航空学会可靠性工程专业委员会第十届学术年会论文集.北京:国防工业出版社，2006.DONG Hai-ping，WEN Yu-quan，CAI Rui-jiao.Study on error of estimator of standard deviation in up-down method test［C］∥Paper Collections of the 10th Annual Seminar of Reliability Committee of Aviation Association of China.Beijing:National Defense Industry Press，2006.(in Chinese)