新型舰炮系统时序化与随机性调度复合供弹方法

葛杨，邱志明，肖亮

(1.武器装备研究院，北京100051;2.哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨150001)

0 引言

大口径舰炮主要执行对岸、对海作战以及防空、反导的战术任务，随着俄罗斯КВР 设计局122 mm、152 mm、155 mm 3 种口径红土地激光制导炮弹和美国洛克希德·马丁公司的155 mm 铜斑蛇激光制导炮弹的研制，新一代舰炮正朝着大威力、高射速、多弹种、弹炮武器相互融合的方向发展。

目前，美国MK45-1 型单127/54 mm 舰炮在满足高速供弹的条件下同时具有自动选择6 种弹药的能力;俄罗斯А-192М 130 mm 舰炮可依据指令自动供、输(包括红土地制导炮弹在内)多种弹药，多弹种兼容发射已成为该炮的主要特点之一［1］;法国“紧凑”型100 mm、50 mm 口径舰炮在3 种弹药之间可实现任意更换，其供、补弹系统具有自动装弹(将炮弹从弹药库输送到活动弯道末端)，又能反向自动退弹的功能特点，供弹率由发射率变化而自动调节，更换弹种的时间只需6 s［2］;作为美国海军新一代主力舰炮AGS 在射速试验中的最大持续射速为10 发/min，急袭射速为8 发/min，可在45 s 或更短的时间内从弹架中取出8 发弹药，并且具有能够从多个弹架中提取多种弹药的能力［3］。分析以上主要型号舰炮的技术特点可以看出:

1)大口径舰炮供、补弹系统应具有向输弹系统和供弹系统进行变速供、补弹和快速更换弹种的能力，才能保证多弹种弹药在系统内的高密度存储、快速更换，在弹位间的准确转移和连续性输送，才能实现系统的最佳供、补弹速率和持续供、补弹速率的结合，提高大口径舰炮快速反应能力和持续作战能力，保证实战条件下大口径的舰炮战术效能的发挥。

2)大口径舰炮供、补弹系统应具有存储、输送、识别的一体化功能，具有针对随机性目标和不确定性因素进行实时判断与多任务决策管理和自动控制的能力，才能满足系统随机性供、补弹要求，合理分配与再分配系统的工作时序，对系统机构进行全局性调度与再调度，保证补弹系统与供弹系统、供弹系统与发射系统同步功能的实现，使舰炮战术效能达到最大化。

因此，连续供、补弹下舰炮系统机构的综合设计需要从系统的连续性时序和随机性调度两方面入手，适应系统机构停、供或供、停的工作特点和弹药阻塞、滞留、转换、退弹和系统故障等随机性因素影响，平衡系统机构连续供、补弹和随机性供、补弹二者的矛盾关系，优化系统设计，提高舰炮的整体作战性能。

1 连续供弹下系统的时序设计

以某口径新型舰炮供、补弹系统(设计供弹速率:制式弹RSP=50 发/min，制导炮弹 Rgp=10 发/min，特种弹Rsp=10 发/min，下同)为例，进行舰炮系统的全局性时序设计。

1.1 单一弹种的供、补弹时序

如图1所示，供弹系统采用模块化存储、平台化补弹、集中式供弹的一体化体系结构。依据弹位、载荷状况、工作步条件对系统采用错时、延时、缩时供弹方法，进行合理分配和动态匹配，工作步平均工作时间满足

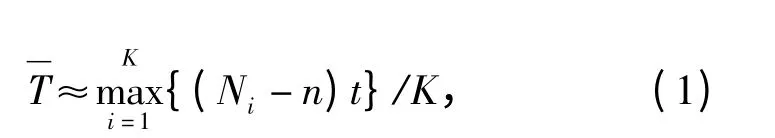
式中:K 为系统工作步数;Ni为步内子工作步数;n为步内子工作步重合数。

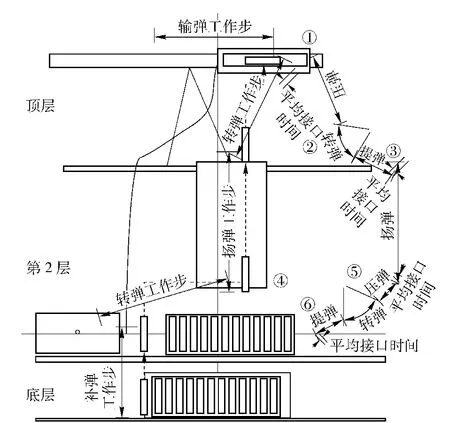
图1 舰炮供弹机器人系统时序工作原理图Fig.1 TO principle of naval gun feeding system

考虑系统:甲板供弹，回转间扬弹，扬弹机扬弹，下、上甲板补弹系统工作任务，由供弹速率R=50 发/min，则系统平均工作时间为1.2 s.设3 步内平均工作时间为0.9 s;3 步内平均调整工作时间为0.1 s;3 步内平均重叠工作时间为0.1 s.系统理想时序设计如图2所示。

由(1)式得

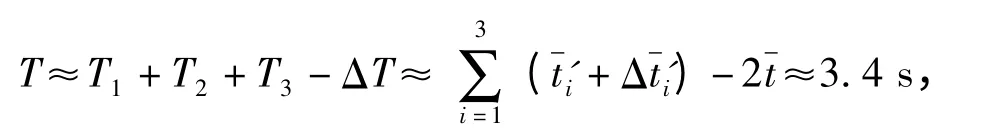
1.2 多弹种弹药的供、补弹时序

为了满足系统快速供弹的有效性，多弹种供弹下，协调供弹、退弹和补弹时间的多工况工作条件进行供弹系统机构时序设计与修改，设平均退弹时间、弹种更换时间、接口时间分别为1 s、4 s、5 s，由(1)式得

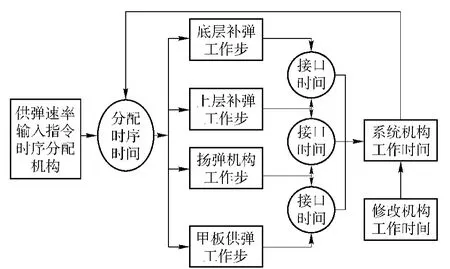
图2 理想时序设计Fig.2 Desired TO design

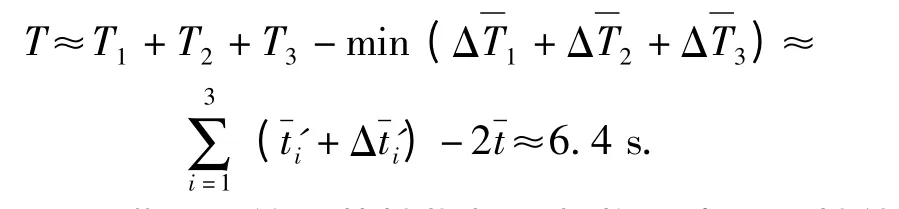
则以满足系统适装性指标和机构动态工作性能指标的要求，缩短供弹系统弹种转换时间和提高平均供弹速率为设计准则进行时序修整，修改后的时序设计结果如图3所示。

图3 修改后的工作时序Fig.3 Modified timing sequence

2 随机调度条件下时序决策与再分配

时序设计中，系统机构出库和入库调度、弹药弹种转换、系统故障的发生过程离散特征明显，对系统状态需要结合系统连续性特征和离散性特征进行系统随机概率事件和元素属性值设定，平衡系统随机性和连续性过程影响，并依据随机性的调度决策对系统时序进行再分配［4］。

2.1 随机调度系统状态分析与设定

如图1所示，机构系统为多层式供、补弹结构，自动弹库包括双层式补弹平台，集中式扬弹机构，参考弹药供、补弹时序，系统工作过程中存在:

1)输送设备可能发生故障，导致弹药滞留;

2)到达和离去事件的发生间隔，退弹时间是离散的、随机的;

3)供弹、补弹指令输出、弹药输送服务开始和结束时刻随机;

4)连续状态下，更换弹退回并重新选择弹种与集中式扬弹机构扬、供弹在线路上发生冲突。

因而，执行供弹、补弹任务时，系统需要综合调度，协调层间、层内弹药运转，解决弹种更换(3 种弹药的存在)，以及弹药供停、供退和退停等冲突。研究该系统连续供、补弹系统弹药循环，考虑系统供弹、退弹、换弹和故障事件的发生，分别以S1，S2，S3和S4表示弹药出循环、回循环、退循环、停循环4 种状态，则离散化时间变量(单位时间内)，2 个相邻时刻间的Markov 系统转移概率，满足［5-6］

式中:Sl为l 时段状态;Sl+1为l+1 时段状态;M 为Markov 系统转移矩阵。

2.2 时序控制系统的随机性概率调度

补弹弹库系统为双层式多任务结构，弹药分布情况为:上层为6 弹药箱(200 发弹，制式弹3 列，特种弹，制导炮弹各1 列);下层为6 弹药箱(100 发弹，制式弹2 列，特种弹和制导炮弹各1 列)，则在弹药配比确定条件下，单一弹种弹药的供弹概率如表1所示。

表1 多层式结构单一弹种弹药输送概率Tab.1 Transferring probability of multi-kind projectiles

2.2.1 系统机构的平均供弹率

单位时间内，考虑下层药库补弹弹药数量满足:X=∑XSP+ ∑Xgp+ ∑Xsp，其中单发弹满足则∑XSP～B(nSP，PSP).同理∑Xgp～B(ngp，Pgp)，∑Xsp～B(nsp，Psp).

又B(n，P)在nP 为常数时近似为正态分布，单发弹药供弹可能性均相同，则E ∑(XSP+Xgp+Xsp)=50，σ2=D ∑(XSP+ Xgp+ Xsp)=(D ∑X )SP+∑Pgp(1- Pgp)+ ∑Psp(1- Psp)=1.5，式中:E(X)为系统弹药补给的数学期望;D(X)为系统弹药补给的方差。

因此，概率分布上系统多种弹药补供弹可近似为正态分布f(50，1.5).

2.2.2 系统的多种弹药Markov 系统转移概率

以平均供、补弹单周期为时间参数，设系统工作平均无故障工作时间MTBF=1 600 h，弹种更换时间为4 s，在多任务模式下优先级为制导炮弹优先(一炮三弹的基本设计原则)和机构工作等概率设计原则下(概率分布依据系统供弹正态分布进行计算):单工作周期内，弹药以0.3 的退弹概率被系统退回;弹药以0.3 的供弹概率，因供输流失于系统外;弹药以0.5 的概率因弹药转换而到子系统外，以0.3 的概率由机构退回而归还系统;弹药直接以0.7的概率供弹而输出系统，又以自身0.1 的概率因故障停留在系统外。则由(2)式知，系统工作相应的转移矩阵为

2.2.3 补弹系统弹药的决策控制

动态的补弹系统模型应充分反映临时实体在系统中历经的过程、永久实体对临时实体的作用，以及它们之间的逻辑关系。

以补弹系统为例建立子系统队列关系，并进行编码，同时为了提高调度效率，避免冲突，建立适应性结构作为补弹机构的暂存机构，决策控制如图4所示［7］。

图4 补弹弹药的决策控制Fig.4 Management of supplied multi-projectiles

双层弹库系统层间补弹时，某时刻系统各工作状态概率表征如下:供弹时退弹时换弹时PS23=故障时PS44=PS11+PS22+PS33，式中:H1、H2为甲板层代号;Sij为弹药状态由i 转换为j.

由(2)式知，以连续调度n 发为例，修改Markov转移矩阵相应的系统转移概率，则某时刻连续补弹下的转移关系满足

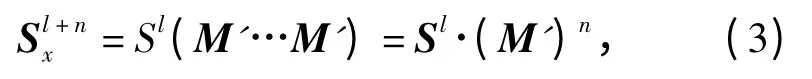
式中:M'为修改后Markov 矩阵;Sl+nx为修改后状态向量。

比较(2)式与(3)式，连续供弹时，系统状态向量发生变化，系统在同时刻、不同工作层进行多弹种弹药补弹时发生层间补弹冲突。

因而，以某时刻Markov 系统转移概率理论为基础，将时序设计原理引入该型舰炮供、补弹系统并进行系统的随机性再调度设计，可以充分优化和提高系统重叠供弹时间，提高系统对弹药的决策和控制能力，则比较层间系统补弹状态矩阵，并由(1)式知，随机性时序工作条件下，系统工作时序条件满足

式中:K 为系统工作步;n 为步内子工作步重合数。

依据效率原则，采用设计适应性机构解决机构供、补弹的冲突问题，建立适应性机构模型如图5所示。对改进后的系统进行动态库调度管理和全系统进行时序优化设计，随机性时序调度后设计系统的全系统时序满足

图5 随机调度下适应性机构Fig.5 Adaptive mechanism in random schedule

依据各弹种弹药平均供弹率计算，弹种更换下供、补弹系统平均工作时序如图6所示，其弹药转换节点平均工作时间分别为tA=6.917 s，tB=15.413 s，tC=18.689 s，tD=5.939 s，tG=8.978 s，tH=10.112 s，其中:A 点和D 点为弹种转换点，B 为弹种转换点，C为供弹输弹转换点，G 点和H 点为两层甲板弹位。

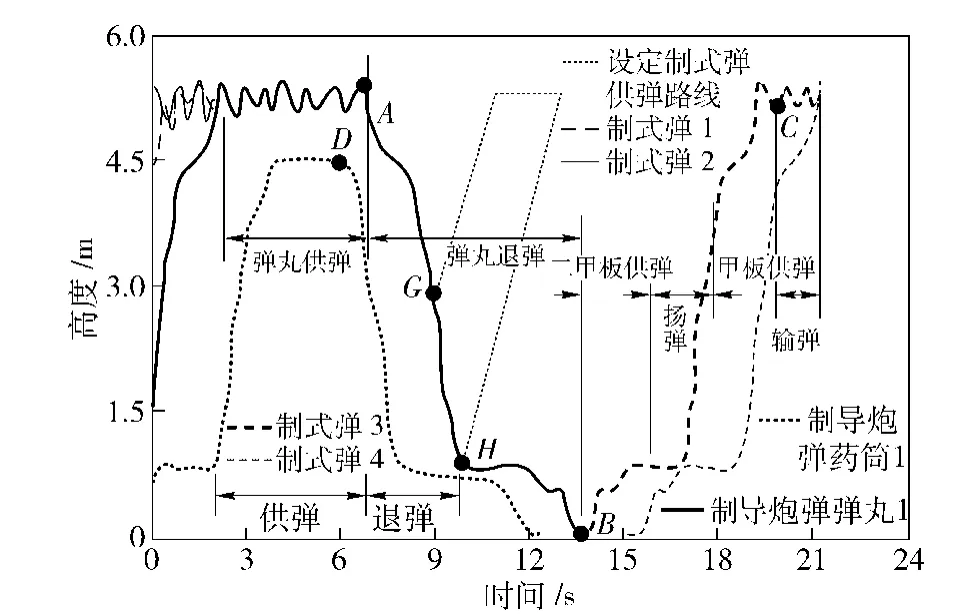
图6 弹种更换平均工作时序Fig.6 Average TO of projectile replacement

3 系统仿真

根据系统特性的不同将工程系统分为连续系统和离散系统［8-10］。依据舰炮时序设计原理，对连续供弹下的系统弹位、工作步、弹药状态和系统出入库调度过程进行基于系统时序分配下的随机调度性能仿真:

1)基于Simulink/MATLAB 控制仿真，建立控制系统的状态调度算法，将模型针对接口动力控制特性，设计程序如图7所示。

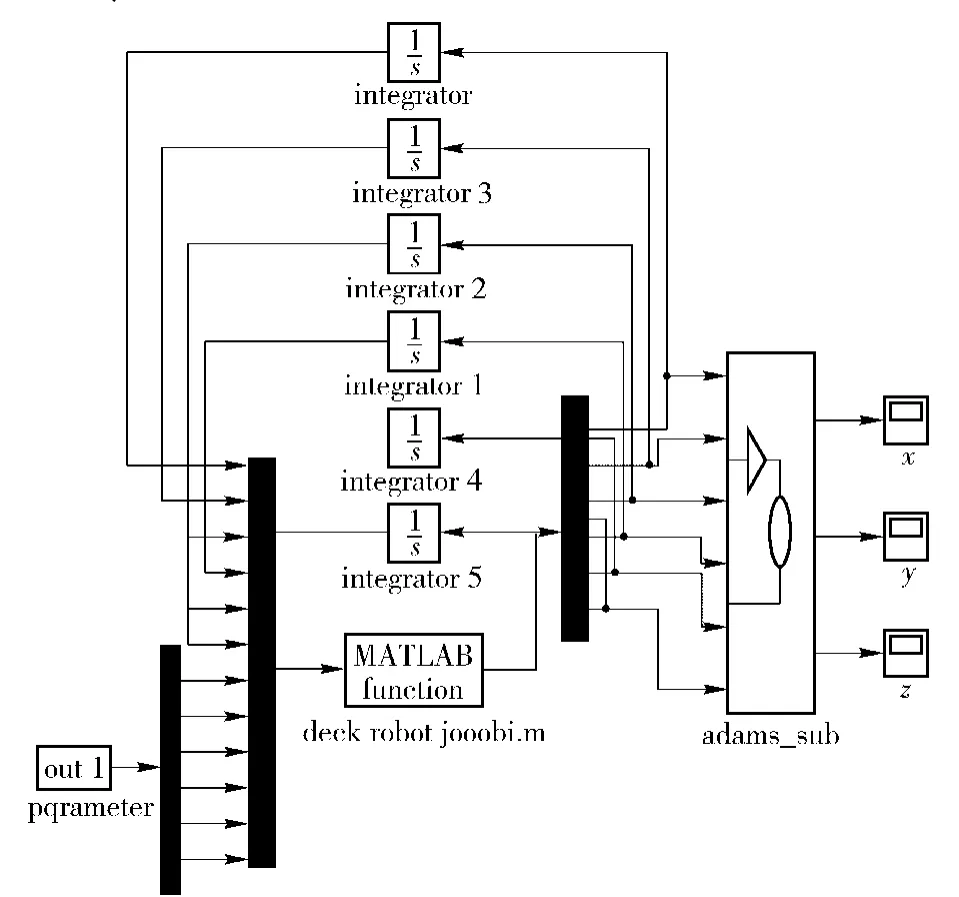
图7 Simulink/MATLAB 的控制仿真Fig.7 Simulink/MATLAB simulation of control system

2)更换弹种过程描述为:将1 号弹箱内的炮弹输出结束，更换输出2 号弹箱内的炮弹，再更换输出3 号弹箱内的炮弹，其中:多弹种弹药输出过程与单种弹出库过程相同;箭头表示炮弹的运送方向。仿真时，对系统弹药供输和弹药的转换进行多体动力学仿真，出库及更换弹种3 种状态下仿真如图8所示。

图8 更换弹种过程仿真状态Fig.8 Simulation for projectile replacement

对某口径舰炮供、补弹系统性能进行仿真，基于上述随机性连续工作过程，随机抽取3 种弹药(制式弹，制导炮弹，特种弹)作为样本，并实施控制，循环调度时序如图9所示。

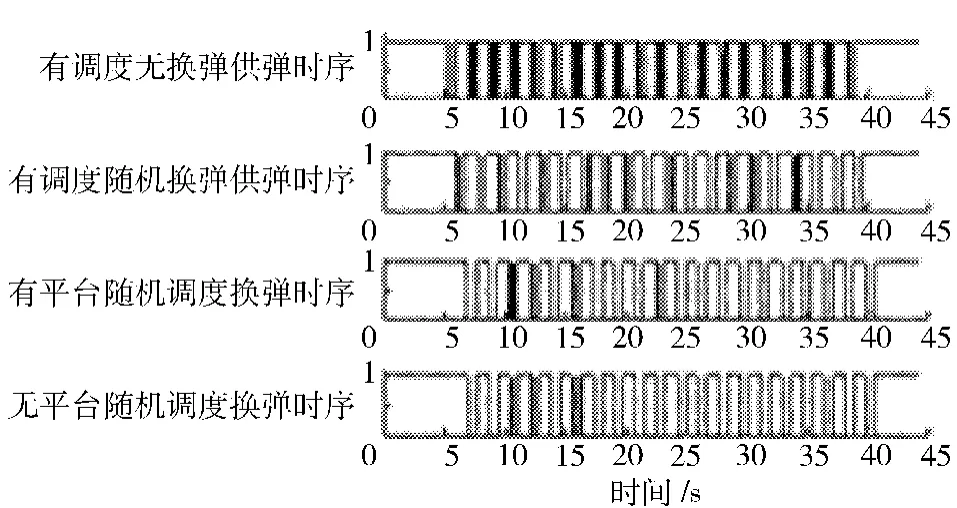
图9 单次循环调度时序图Fig.9 Management plot of time sequence

经过20 次测量，并对时序节点数据进行采集和拟合处理，结果如下:

1)弹种更换规律符合系统总体调度控制率，无换弹的全系统工作时间(整装制式弹，制导炮弹，特种弹)与弹种更换条件下的全系统工作时间:无调度供弹时=10.858 s，随机调度供弹时=16.974 s.

2)对机构进行优化设计，设置工作平台和“栈”式临时补弹机构，动态库随机调度下的弹种转换工作时间:无平台时t=51.039 s，有平台时=46.173 s.

3)进行动态库随机调度，多弹种单发弹的全系统平均工作时间:46.039 s.

对比和分析仿真结果可以看出:在连续周期供弹下，单发制式弹、无换弹下全系统工作时间为1.08 s，供弹速率为55 发/min，随机性换弹条件下平均供弹速率达到35 发/min;无临时补弹平台机构系统弹种转换时间为5.1 s，采用临时补弹平台后输送弹种转换时间由6.4 s 提高到4.6 s，提高补供弹机构弹药更换和补给工作效率20%～30%.

4 结论

依据某型舰炮补弹系统的连续性和离散性复合工作特点，本文提出时序化供弹与随机性调度复合设计方法，并将该方法应用于某型舰炮的弹库系统设计中，通过对该型舰炮的弹库系统虚拟样机仿真可得出如下结论:

1)采用该方法在随机性条件下进行大基数弹库兼容供弹、补弹和换弹机构设计可以明显提高系统弹药更换和补给效率。

2)采用该方法可以明显改善系统随机性供弹和换弹性能，降低解决系统层间与层内供弹冲突问题，减少舰炮供、补弹间隔时间，提高舰炮的战术效能。

3)本文方法也可为多层次系统结构性能优化和大基数、智能化、多样化输送机构控制，提供一种参考方法。

References)

［1］ 孙世岩，邱志明.舰炮武器系统优化配置方法比较研究［J］.兵工学报，2007，28(7):991-998.SUN Shi-yan，QIU Zhi-ming.A comparison study on optimal configuration methods of naval gun weapon systems［J］.Acta Armamentarii，2007，28(7):991-998.(in Chinese)

［2］ Dubin Henry，Sebastiani Lambert，Taniec Cyrus.Integrated modeling and simulation into the US Army operational test and evaluation process［C］∥Proceedings of High Performance Computing Workshop.Boston:IEEE，1998:1-9.

［3］ Wolcott，Robert S，Bishop Bradley E.Cooperative decision-making and multi-target attack using multiple sentry guns［C］∥Proceedings of the Annual Southeastern Symposium on System Theory.Annapolis:IEEE，2009:261-265.

［4］ Jean Damay，Alain Quilliot，Eric Sanlaville.Linear programming based algorithms for preemptive and non-preemptive RCPSP［J］.European Journal of Operational Research，2007，182(3):1012-1022.

［5］ James Forbes，Christopher Damaren.Design of gain-scheduled strictly positive real controllers using numerical optimization for flexible robotic system［J］.Dynamic，System，Measure and Control，2010，132(3):503-510.

［6］ 何斌，芮筱亭，陆毓琪.多体系统离散时间传递矩阵法与有限元法混合方法［J］.南京理工大学学报:自然科学版，2006，30(4):998-1021.HE Bin，RUI Xiao-ting，LU Yu-qi.Hybrid method of discrete time transfer matrix method for multi-body system dynamics and finite element method［J］.Journal of Nanjing University of Science and Technology:Natural Science，2006，30(4):998- 1021.(in Chinese)

［7］ Habiro Yoshiaki，Hori Noriyuki.A new discrete-time logistic equation having no overshoot and no chaos［C］∥Proceedings of ICROS-SICE International Joint Conference.Fukuoka:Elsevier，2009:964-969.

［8］ Wang Geng，Kondak Konstantin，Marek Musial，et al.Development of an autonomous flight control system for small size unmanned helicopter based on dynamical model ［J］.Journal of Shanghai Jiaotong University，2007，E-12(6):744-752.

［9］ Michael Pinedo.调度:原理、算法和系统［M］.第2 版.北京:清华大学出版社，2007.Michael Pinedo.Scheduling-theory，algorithms and systems［M］.2nd ed.Beijing:Tsinghua University Press，2007.(in Chinese)

［10］ Forget Julien，Boniol Frédéric，Grolleau Emmanuel，et al.Scheduling dependent periodic tasks without synchronization mechanisms，real-time technology and applications［C］∥Proceedings of the 16th IEEE Real-Time and Embedded Technology and Applications Symposium.Stockholm:IEEE，2010:301-310.