压铸充型过程的SPH方法建模及数值模拟*

曹文炅 周照耀 何毅 吴菲

(1.华南理工大学机械与汽车工程学院，广东广州510640;2.广州华立科技职业学院，广东广州511325)

高压铸造(High-Pressure Die Casting，HPDC)是将金属液体在高压条件下以极高的速度充填模具型腔，并在浇口处保持高的挤压力而使金属液体凝固成型的过程.该工艺能够成型具有高精度、高表面质量、高强度的零件，因此广泛应用于汽车、航空航天、通信等领域.然而金属液充填型腔过程中易形成气孔缺陷，该缺陷是影响压铸件废品率的主要因素之一［1］.通过计算机数值模拟对金属液充型过程进行分析，能够有效把握充型状态的合理性，从而降低铸件废品率，提高产品质量.目前，研究者主要采用基于欧拉描述下的计算流体动力学方法，即通过有限差分法、有限体积法和有限元法等离散求解域，并求解相关控制方程，获得金属液在模腔内的运动规律.然而基于欧拉描述的流体计算模型不能直接处理自由表面、运动物质交界面等问题，而需引入体积分数方程等手段进行特殊处理，具有一定的局限性.此外，上述方法的求解精度均依赖于网格的质量，而对于复杂形体的网格划分十分困难，故往往因网格畸变严重而造成求解精度降低甚至发散.

近年来无网格法备受人们关注，其中一种被称为光滑粒子流体动力学(SPH)的方法在天体物理、计算流体动力学等方面得到了较深入的发展.该方法最早由 Lucy、Gingold 以及 Monanghan 提出［2-3］，它通过基于纯拉格朗日描述的一系列粒子离散求解域，粒子和粒子之间通过核函数建立相互作用，从而彻底取代了网格.对流动前沿的计算是评价计算模型准确性的关键指标，由于SPH算法的纯拉格朗日特性，对于自由表面的追踪可以通过粒子本身的位置确定.而在压铸成型中，金属液的自由表面对产品质量的影响极为关键，因此SPH方法在压铸过程模拟中具有一定优势.

目前SPH方法在压铸方面的研究还相对较少，主要集中于Cleary所在的 CSIRO实验室.Cleary等［4-5］分别采用SPH方法和体积函数(VOF)方法计算了某铸件充型过程并进行了对比，同时建立了透明模具进行水流注射实验，通过高速摄像的方法捕捉充型过程的流态，从而证明了SPH方法的准确性.文中建立了压铸过程SPH方法计算模型，并对压铸过程所需的浇口处入流边界条件设置方法进行了研究，利用Fortran语言编制计算代码并对Schmid等［6］给出的验证模型(简称Schmid验证模型)充型过程进行了分析.

1 SPH方法概述

SPH方法是一种纯拉格朗日方法，采用粒子加权求和的形式对场函数进行近似.粒子本身除包含位置、速度、压力等场量之外，还包含了材料质量、密度等信息，从而完整表述了系统的状态.SPH模型建立的核心包括积分表示和粒子表示两部分.一般而言，对于函数能够用其自身的积分近似表示，如式(1)所示:

式中:x'为点x领域内某点;W(x－x'，h)称为光滑函数或者核函数，其实质为广义的狄拉克函数，文献［3］中证明了当核函数具有紧支性、归一性和偶函数的特征时，该近似式具有二阶精度;h为光滑长度，表征了点x处采用核近似的空间范围，该空间范围即为积分区域Ω，也称为支持域.

式(1)可转化为点x处粒子i的支持域内所有粒子叠加求和的离散化形式，这一过程即为粒子近似.若用粒子体积ΔVj来取代在前面积分中粒子j处的无穷小体元dx'，并且将粒子体积ΔVj表示为粒子质量mj与密度ρj的商的形式，最终可将式(1)整理为如下的粒子求和形式:

同样，对于梯度函数，也可利用核函数的梯度构建求和表示式:

式中:N为粒子i的支持域内粒子的总数(不包括粒子i).通过式(2)及式(3)能够将空间内某一点的函数值及梯度表示为支持域内粒子函数值加权求和的形式，图1反映了核函数、支持域、光滑粒子的关系.文中选取了B样条函数作为光滑函数进行求解.该样条函数在狭窄的紧支域内，与高斯型函数类似，具有较好的光滑特性，同时比高斯型函数更容易计算，其特性在文献［3］中有较详细的论述.

图1 核函数与粒子的关系Fig.1 Relationship between kernel function and particles

2 压铸充型过程的SPH方法建模

压铸充型过程中，金属液的流动行为复杂，具有流体的分离和汇聚以及液滴的飞溅甚至雾化等特征，采用基于欧拉描述的网格方法很难对这一过程进行准确模拟，而SPH方法通过求解拉格朗日描述下的控制方程，能够较好地处理流体的分离和汇聚、不连续自由表面等问题.

2.1 控制方程的SPH方法离散

采用式(2)及(3)对拉格朗日描述下的控制方程离散并进行整理，可得连续性方程、动量守恒方程、能量守恒方程的 SPH表示式(式(4)－(6))［7-8］.

式中:m、ρ、v、p、U 分别代表粒子的质量、密度、速度、压力及内能;下标i与j代表相互作用的一对粒子编号，各变量若下标为i则表示该变量属于粒子i，若下标为j则表示该变量属于粒子j;为粒子 i与粒子j的相对速度;εαβ为应变速率张量函数;上标α、β表示坐标方向;μ为动力黏度系数;t为时间变量.式(5)中，等式右端第一项求和部分为流体压力对加速度的贡献值，第二项为粘性力对加速度的贡献值.同样地，式(6)中等式右端第一项求和部分为压力功，第二项为粘性耗散项.式(5)及(6)中的压力p由流体的状态方程求得，对于微可压缩流体，采用人工压缩率方法表征压力p的变化，其表达式为

式中:K参数用于将密度变化量限制在一定范围内，从而保证模型为微可压缩模型;ρ0为材料的初始密度;γ为常数，一般取γ=7.

2.2 壁面边界条件

在压铸充型过程的SPH分析中，需要进行模具型腔壁面的粒子化处理，从而为金属液充填提供壁面边界条件.由于模具型腔的复杂性，壁面边界条件的建立需要具有一定的灵活性以保证对复杂型腔壁面的拟合.一种方法是通过靠近边界的粒子建立对称于边界的虚粒子，将所有的虚粒子赋予与边界处等值的全部变量值，并沿虚粒子所构成的特殊边界积分来计算内部粒子处的值.由于该方法所用的虚粒子需要通过壁面镜像靠近壁面的粒子而获得，在一些简单的几何模型中能够方便实现，但模具型腔壁面的几何形状往往十分复杂，虚粒子的建立十分困难.文中采用 Monaghan等［9］提出的边界排斥力模型，在固定壁面上布置了一层壁面粒子用于对邻近边界的粒子施加强排斥力，从而阻止邻近边界的这些粒子穿透边界.这种方法只需要在模具型腔表面布置一定密度的粒子，灵活性强并易于实现.排斥力Fij的数学模型为

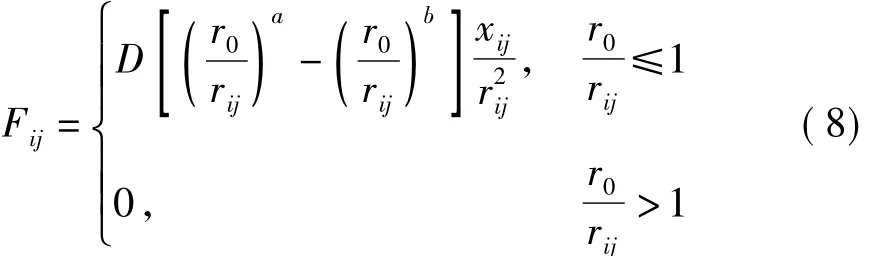
式中:参数a与b取值一般分别为12和4;D取与速度最大值的平方相等的量级;r0为截止半径，一般取与初始粒子间距相近的值.

2.3 入流边界条件

为保证计算效率，压铸充型数值模拟的计算域通常只包括由浇口位置开始至整个模具型腔部分，而不需要计算进入浇口之前的金属液流态.这表现为在浇口位置，单位时间内具有一定质量、压力的流体以一定速度进入计算域，因此需要在浇口位置建立入流边界条件.文中将计算域划分为流体区域和入流边界区域两部分，各区域内粒子分别为流体粒子和入流区域粒子，如图2所示.

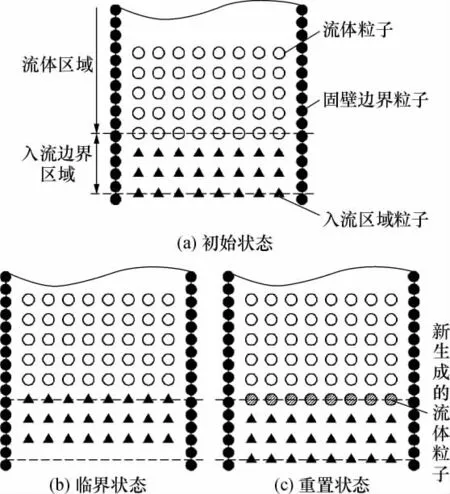
图2 入流边界条件的实现Fig.2 Realization of inlet boundary conditions

入流边界的实现过程为:初始状态如图2(a)所示，入流区域粒子处于一部分流体粒子的支持域内，并参与到流体粒子守恒方程的计算中.入流区域粒子一般设置为2至3层，这一方面能够保证流体粒子的求解精度，另一方面能够防止流体粒子反向穿出入流边界.计算中仅对入流区域粒子的位移进行时间步更新，而其速度、压力值为设定值(可由压铸工艺的p-Q2图获得，Q为流量).当入流区域粒子运动至入流边界区域与流体区域的交界处时(如图2(b)所示)，对入流区域粒子进行重置，使之回归于初始状态，同时在交界处生成一层新的流体粒子(见图2(c)).对新生成的流体粒子的初始速度、初始压力赋予与入流区域粒子相等的值，在之后的计算中按照守恒方程获得.至此完成入流边界的一次循环，并进入下一相同的循环过程.通过这种方法建立的入流边界条件具有与欧拉方法的入流边界相同的效果，入口处的速度、压力具有连续性，并能够按照实际情况进行参数的选择.

2.4 计算代码的实现

文中采用Fortran语言编写计算代码，在CVF6.6环境中进行编译计算.图3为求解压铸充型过程的SPH计算程序结构.具体步骤如下:

(1)初始化模型.定义计算所用的各个变量，对壁面边界和入流区域进行粒子划分.粒子划分可通过程序实现，也可通过外部文件读入.

(2)进入主循环部分.判断当前时刻相互作用的粒子对，并计算光滑函数及其梯度函数.

(3)根据连续性方程(4)计算密度变化率，通过状态方程(7)计算压力.求得的压力值代入动量守恒方程(5)和能量守恒方程(6)，获得动量变化率和能量变化率;通过式(8)求解壁面边界作用力并附加到粒子动量变化率中.

(4)对步骤(3)获得的密度变化率、动量变化率、能量变化率等进行时间积分，得到粒子新的密度、速度、内能、坐标.时间积分采用预测－校正法.

(5)输出当前时间步的结果，同时进行入流边界的判断和更新，并返回步骤(2)，进行下一时间步的计算.

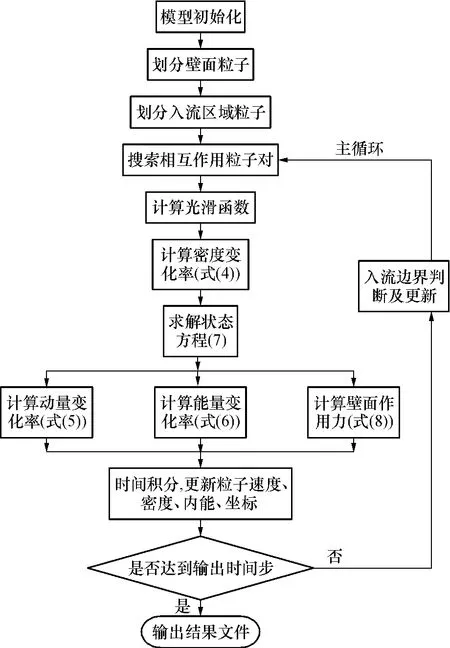
图3 压铸充型过程的SPH计算流程图Fig.3 Flow chart of SPH in HPDC process

3 压铸充型SPH计算模型的验证

3.1 几何模型及计算参数

为研究计算模型的准确性，文中采用SPH方法对Schmid验证模型进行了计算.计算模型为一圆盘型中孔零件，Schmid等［6］研究的流体为着色水，模具采用透明的有机玻璃，并用高速摄像机记录了压射过程.由于水具有与金属液近似的运动黏度，该实验能够表征金属液在相同模具中的流态.计算中所用流体密度、黏度等参数与液态水相同，入流速度为18m/s，模型厚度为2 mm，其余尺寸如图4所示.离散后流体粒子间距为0.8mm.固壁边界粒子间距为0.4mm，取流体粒子间距的一半能够有效防止壁面穿透.

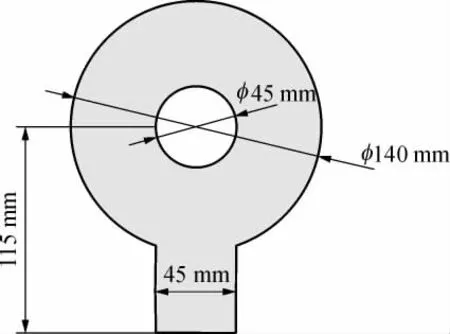
图4 Schmid验证模型Fig.4 Schmid's verification model

3.2 SPH方法计算结果

图5为充型过程中粒子的分布.为了表征粒子入流的先后顺序，同时追踪前沿流体的流动状态，在图5中采用灰度显示粒子入流的先后顺序，灰度越高的粒子越早进入模腔，反之则为后续生成并进入型腔的流体粒子.为研究流体冲击模具型芯后分离的过程，对已进入型腔的流体前沿部分的粒子按照对称关系区分为左右两部分，并使流体前沿右半部分粒子灰度深于左半部分，如图5(a)所示.

图5 SPH方法的计算结果Fig.5 Calculation results of SPH method

充型过程主要包含4个阶段，分别与图5中的各个分图对应.第1阶段，流体通过流道进入型腔并正面冲击型芯，在型芯作用下被分为两股支流，开始向型芯两侧流动，如图5(a)所示;第2阶段，被型芯分离的两股支流继续充填型腔，在接触型腔外轮廓后再次分离，形成如图5(b)所示的4组支流Ⅰ、Ⅱ、Ⅲ、Ⅳ，各支流均沿着型腔外轮廓流动;第3阶段，支流Ⅰ与支流Ⅱ汇合，并回流冲向型芯上部，支流Ⅲ与支流Ⅳ沿型腔外轮廓流动，并与流道处进入型腔的流体汇合，如图5(c)所示;第4阶段，汇合后的支流分别形成如图5(d)所示的4个空穴，随着流体不断注入型腔，空穴的尺寸逐渐缩小并完成充型过程.

3.3 有限差分法计算结果

为了说明SPH方法的拉格朗日特性在自由表面计算的优势，文中采用基于欧拉描述的有限差分方法(FDM)对该模型进行了计算，对自由表面计算采用VOF方法处理.图6为充型过程的体积分数函数分布，用以表征自由表面的位置.

图6 有限差分法计算结果Fig.6 Calculation results of FDM

3.4 计算结果比较与分析

图7为Schmid验证模型的实验照片，实验结果对应于计算结果的第2－4阶段.分别将采用SPH方法计算的结果与验证模型的实验结果及采用FDM计算的结果对比，可以看出通过SPH方法所获得的计算结果与Schmid验证模型的实验结果一致，而FDM在后期充填计算中所得结果与实验结果不符.由于文中建立的计算模型是由浇口位置开始计算，Schmid验证模型是以流体进入型腔开始计时，因此两种方法计算的时间滞后于验证模型2 ms左右.

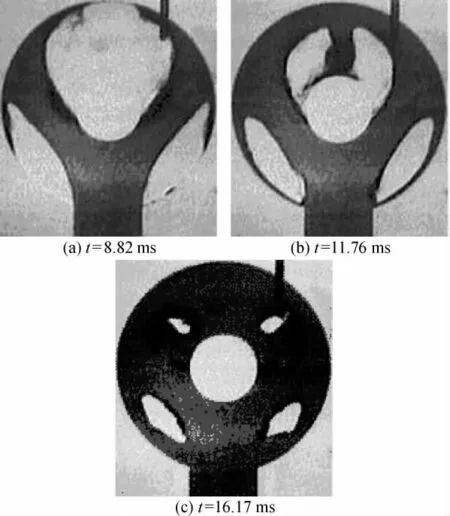
图7 Schimid验证模型的实验结果Fig.7 Experimental results of Schimid's verification model

在第1阶段，两种方法计算结果相近，均能够获得流体冲击型芯后的形态;而在流体被型芯分离成两股支流并进入第2阶段充填后，两种算法出现了差异.采用FDM所获得的两股支流在绕过型芯后的流动方向与垂直方向夹角在10°以内(图6(b)所示)，而SPH方法获得的两股支流与垂直方向的夹角在40°左右，更接近于实际验证模型(图7(a)所示).第3阶段充填中，FDM获得的流体分布集中于模腔上部，回流的支流Ⅲ及Ⅳ的流动滞后于实际模型，自由表面的计算也存在较大误差，如图6(c)所示.这导致在第4阶段充填中，FDM不能准确获得下部两个空穴的形状和位置，如图6(d)所示.造成FDM计算误差的原因一方面在于通过体积函数方程所获得的自由表面界限模糊，自由表面发展的求解不稳定，另一方面是正交化的有限差分网格在离散圆形模具壁面时形成锯齿形结构，影响了求解的稳定性.相比而言，SPH方法能够通过粒子本身准确表现自由表面的形状和分布.

通过图5所示粒子的灰度分布可以看出，第2阶段及第3阶段所形成的支流均为第1阶段中所标记的流体前沿部分发展而成，第4阶段中所形成的空穴也是由流体前沿部分包围而成，并呈旋流状.流体前沿经历了最长的充型流程，这在实际压铸中易产生冷隔、流痕等缺陷.最终SPH方法获得的空穴的位置及大小(图5(d))均与验证模型(图7(c))吻合.实际压铸中，空穴部分是产生气孔缺陷的位置，对空穴位置和大小的准确计算有助于定量预测压铸件气孔缺陷.

4 结语

文中建立了压铸充型过程的SPH方法控制方程，引入Monaghan边界模型建立了型腔壁面边界条件，通过划分入流区域粒子和流体粒子满足了入流边界条件，利用Fortran语言编写了SPH计算代码，并计算了Schmid验证模型.所获得的结果与采用FDM计算的结果以及实验结果进行了对比.采用对流体粒子的灰度表示方法研究了流体前沿部分在充型过程中的分布，并获得了充型形成的空穴的形状和大小.由于SPH方法不需要借助网格离散求解域，避免了网格畸变以及对边界描述不精确造成的计算误差，同时SPH方法具有纯拉格朗日特性，能够通过粒子本身确定自由表面，因此采用SPH方法计算的结果准确表现了充型过程中流体的分离、汇聚以及自由表面的形状和分布.在实际充型中，金属液流动还受型腔残余气体、金属液温度变化等因素的影响，后期研究中，可在SPH流场计算模型中加入气液两相流模型以及温度场计算模型，从而获得更可靠的模拟结果.

［1］ 柳百成.铸造工程的模拟仿真与质量控制［M］.北京:机械工业出版社，1997:80-112.

［2］ 刘桂荣，顾元通.无网格法理论及程序设计［M］.王建明，周学军，译.济南:山东大学出版社，2007:24-32.

［3］ Liu G R，Liu M B.Smoothed particle hydrodynamics:a meshfree particle method［M］.Singapore:World Scientific Publishing Co Pte Ltd，2003:33-159.

［4］ Cleary P，Ha J，Vladimir Alguine，et al.Flow modelling in casting processes［J］.Journal of Applied Mathematical Modelling，2002，26(2):171-190.

［5］ Cleary P，Prakash M，Ha J.Novel applications of smoothed particle hydrodynamics(SPH)in metal forming［J］.Journal of Materials Processing Technology，2006，177(3):41-48.

［6］ Schmid M，Klein F.Fluid flow in die cavities-experimental and numerical simulation［C］∥International Die Casting Congress and Exposition.Indianapolis:NADCA 18，1995:93-99.

［7］ Liu M B，Xie W P，Liu G R.Modeling incompressible flows using a finite particle method［J］.Applied Mathematical Modelling，2005，29(12):1252-1270.

［8］ Monaghan J J，Kocharyan A.SPH simulation of multiphase flow［J］.Computer Physics Communications，1995，87(2):225-235.

［9］ Monaghan J J，Kajtar J B.SPH particle boundary forces for arbitrary boundaries［J］.Computer Physics Communications，2009，180(10):1811-1820.