用平动惯性力求解力学问题的讨论*
2011-01-24许新胜张雪
许新胜 张雪
(安徽师范大学物理与电子信息学院 安徽 芜湖 241000)
牛顿第二定律是经典力学的核心,仅成立于惯性系[1].我们知道,对于地面上的宏观低速运动,在一定精度范围内,地球以及地球上相对于地球静止或做匀速直线运动的参照系都可看成惯性系,而相对于地球有加速度的参照系是非惯性系.对于一些复杂的运动,如果相对于地面的绝对运动比较复杂,物理图像不太清楚,这时可以考虑在非惯性系中处理问题.但是,在非惯性系中处理力学问题就要牵涉到惯性力.
1 平动非惯性力的应用注意事项
设非惯性系的牵连加速度为a牵,物体相对非惯性系的加速度为a相,则物体相对惯性系中的绝对加速度为
a绝=a相+a牵
(1)
如果物体质量为m,受到的合外力为F,则由牛顿第二定律可知
F=ma=m(a相+a牵)
(2)
(2)式改写成
F+(-ma相)=ma牵
(3)
令F惯=-ma相
(4)
则有F+F惯=ma牵
(5)
(5)式即平动非惯性系中的“牛顿第二定律”[2].其中,F惯大小为物体的质量与非惯性系加速度a相的乘积,方向与非惯性系平动加速度a相相反.非惯性系中的牛顿第二定律表明,物体的质量与相对非惯性系的加速度的乘积等于物体受所有外力(包括惯性力)的合力.
应用惯性力,需要注意以下几点:
(1)惯性力是一种假想的力,没有施力物体,也没有反作用力;
(2)惯性力与其他实际作用的力,如重力、拉力、弹力等,地位相同;
(3)惯性力能做功、有冲量,在非惯性系中引入惯性力后,动能定理、动量定理依然成立.
下面举几个在非惯性系中引入惯性力来求解力学问题的具体实例.
2 平动非惯性力的应用举例
【例1】如图1所示,在光滑水平桌面上放有一质量为M的光滑斜面体A,其光滑斜面上端放一质量为m的小物块B(可视为质点),斜面倾角为θ.试求小物块B从A顶端下滑到底端过程中两者之间的相互作用力.
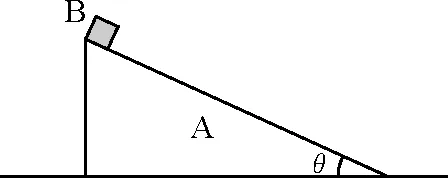
图1
解析:斜面体A不固定,使得小物块B在沿斜面下滑的过程中还会跟随斜面体A向左运动,小物块B相对地面的运动比较复杂,物理图像不太清晰.下面以斜面体A为参照系来考察小物块B的运动从而求解.由于斜面体A有向左的加速度,故求解过程中需要引入惯性力.
设A与B之间的相互作用力为N,A相对地面的加速度为a相,则在斜面体参照系中,B还受惯性力F惯作用,如图2所示.即
F惯=-ma相
(6)
对A,由水平方向的牛顿第二定律可得
Nsinθ=Ma相
(7)
对B,在斜面体A参照系中,沿垂直于斜面的方向小物块受力平衡,有
N+F惯sinθ=mgcosθ
(8)
由(6)、(7)、(8)式可解得
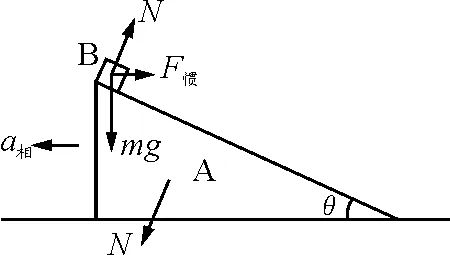
图2
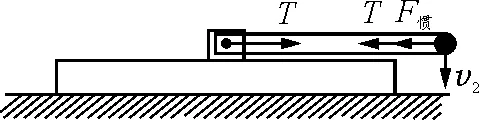
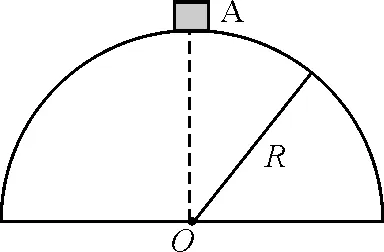
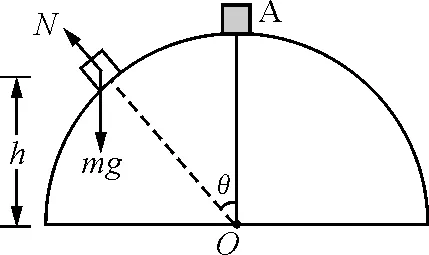
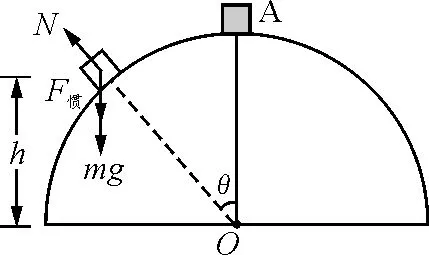
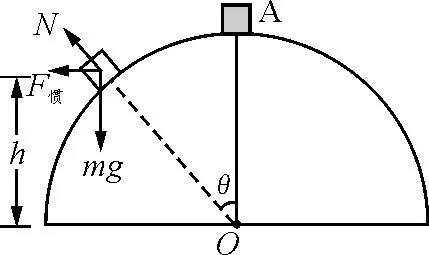
【例2】如图3所示,质量为M的金属板置于光滑地面上,板中央有一光滑转动轴O,轴上连着一根长为L的轻杆,杆的上端固定有一质量为m的小球,且m 图3 解析:系统水平方向不受外力,初始状态系统水平动量为零,又由于杆不可伸长,末状态球与金属板两者水平速度相同,设共同的水平速度为v1,由动量守恒定律可知 (M+m)v1=0 (9) 即 v1=0 设小球竖直速度为v2,由于地面支持力及杆中内力不做功,由机械能守恒定律可得 当前城市规划由于建设速度过快,造成大量的噪音污染和城市建筑垃圾的污染,这些污染造成了城市空间的紧张,尤其是城市建筑垃圾的堆积问题。良好的生态环境是城市发展的基础条件,没有了生态环境,城市建设便无从谈起。同时,良好的生态环境也是评价一座城市是否适宜人们居住的一个重要标准。城市空间是否合理,城市交通是否便利,这些因素常常被人所重视,被认为是城市居住的重要条件,实际上生态环境的优劣才是决定城市是否宜居的根本标准。 (10) 对于杆转过90°时的末态,m相对M的运动可看作转动,转动速度为v2,此时杆中有张力设为T,如图4所示,M加速度不为零,以M为参照系,球还受到水平向左的惯性力作用.于是有 (11) 又由牛顿第二定律可得 (12) 由(10)、(11)、(12)式解得 图4 【例3】一个小滑块放在半径为R的光滑半球顶部,如图5所示.由于轻扰,它开始由静止下滑.求在下列情况下,它离开球面时,离半球底面的高度h. 图5 (1)半球面以10 m/s 的速度匀速上升; 图6 (1)半球面匀速上升时,半球面为惯性系.滑块在半球上滑动时的受力如图6所示,由动能定理及牛顿第二定律可得 (13) (14) 设脱离位置对应的角度为θ0,此时 N=0 (15) 由(13)、(14)、(15)式解得 即脱离时 图7 (2)半球面匀加速上升时,半球面为非惯性系,滑块在半球面上滑动时要受到向下的惯性力的作用,如图7所示,即 (16) 由动能定理及牛顿第二定律可得 (17) (18) 设脱离位置对应的角度为θ0,仍有 N=0 (19) 由(16)~(19)式解得 即脱离时 (3)半球面匀加速向右运动时,半球面为非惯性系,滑块在半球面上滑动时要受到向左的惯性力的作用,如图8所示,即 (20) 图8 另外,由动能定理及牛顿第二定律可得 (21) (22) 设脱离位置对应的角度为θ0,仍有 N=0 (23) 由(20)~(23)式解得 cosθ0=0.81 或 cosθ0=0.44 cosθ0=0.44 不符合实际意义,故可舍去.于是小球脱离球面时有 h=0.81R 从上述几个典型的例子可见,小物块或小球相对惯性系(地面)的运动都很复杂,物理过程难以把握,若在地面惯性系中求解有一定的难度.但在平动非惯性系中,引入惯性力,则物理图像变得清晰,物理过程变得容易理解,平衡方程或圆周运动的牛顿第二定律就可以应用,从而使问题的求解变得简单. 参考文献 1 程守洙,江之水.普通物理学(第五版).北京:高等教育出版社,1998 2 周衍柏.理论力学教程(第三版).北京:高等教育出版社,2009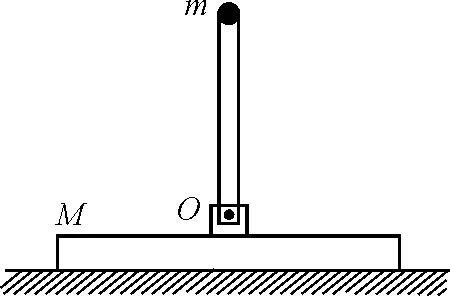
3 小结
