达朗贝尔原理在刚体动力学中的简单应用

徐仁杰

(江苏省海安高级中学 226600)

在动力学问题中，涉及非惯性参考系常引入惯性力，这样非惯性系的问题可以用牛顿运动定律来解决，这种思想源于达朗贝尔原理.高中物理竞赛研究较多的是质点惯性力问题，对于质点系的惯性力很少涉及，本文借助于几个常见模型分析刚体定轴转动和平面运动中的达朗贝尔原理.

1 质点的达朗贝尔原理

作用在质点上的主动力、约束力和它的惯性力在形式上组成平衡力系，这就是质点的达朗贝尔原理，写成方程：F+FN+FI=0，FI=-ma称为质点的惯性力.引入惯性力的概念可以使动力学问题借用静力学的理论和方法求解，具有很多优越性，下面举一例说明.

例1 均匀半圆形金属拱架ABC的圆心在O点，质量M=1000kg.A端用铰链连接，B端放在滚珠上，有一质量m=500kg的小物块从最高点C无摩擦滑下，如图1所示，求当物体滑到D点时(∠COD=30°)，求A、B两支点对拱架的约束力.

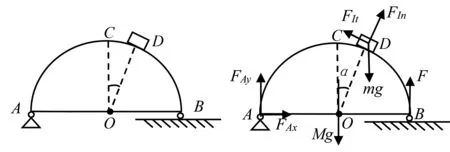
图1 图2

小物块做圆周运动，可看作质点，具有切向加速度at和法向加速度an，分别引入惯性力FIt和FIn.取整体为研究对象，列出力和力矩平衡方程：

FAx+FInsinα=FItcosα

FAy+FB+FIncosα+FItsinα=(M+m)g

FAyR-FItR-FBR+mgRsinα=0

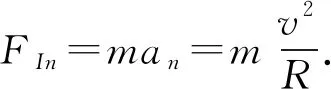
由以上各式解得：

FAy=FB=6295N,FAx=1495N.

点评引入惯性力后，小物块的受力在形式上达到平衡，可以与拱架整体分析建立平衡方程，避免了对内力的分析.

2 质点系的达朗贝尔原理

质点系的达朗贝尔原理表述为：质点系中每个质点i上的主动力、约束力和它的惯性力在形式上组成平衡力系，写成方程Fi+FNi+FIi=0，FIi=-miai是质量为mi的质点的惯性力.

空间任意力系平衡的充要条件是力系的主矢和对任一点O的主矩等于零，由于质点系内力总是成对出现，且等大、反向、共线，内力产生合力和合力矩为零，即∑Fi内=0，∑MO(Fi内)=0，质点系平衡方程写成：∑Fi外+∑FIi=0，∑MO(Fi外)+∑MO(FIi)=0.

质点系内每个质点都有各自的惯性力，受力复杂，在实际应用中，对于惯性力系通常做简化处理.

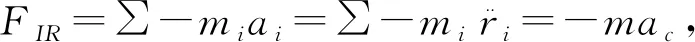
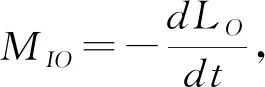
刚体做平移运动时，对质心的动量矩LC=rc×mvc≡0,若选质心为简化中心，主矩为零，因与质点的应用相似，不做详细分析.下面以刚体定轴转动和平面运动为例分析惯性力系的简化.

2.1 刚体定轴转动惯性力系的简化

图3

得到MIx=∑miriαcosθi·zi+∑-miriω2sinθi·zi=α∑mixizi-ω2∑miyizi.

类似的，惯性力系对y轴和z轴的矩分别为

若刚体有垂直于z轴的质量对称面，把简化中心O取在该平面与z轴的交点，则∑mixizi=0，∑miyizi=0.惯性力系对O点的主矩为：MIO=MIz=-Jzα，这种情况下惯性力系处理起来简单了很多.

例2 如图4所示，均质杆OA长2l，质量m，绕着通过O端的水平轴在铅锤面内转动.当转到与水平线成θ角时，角速度为ω.求此时O端的约束力和角加速度α.

图4 图5

OA杆做定轴转动，且有垂直于转轴的质量对称面，选取O点为简化中心，受力分析如图5所示，根据达朗贝尔原理建立平衡方程：

MIO=mglcosθ

求得FOx=-mlαsinθ-mω2lcosθ，

点评由此题可见，对垂直于转轴有质量对称面的定轴转动刚体，选择质量对称面与转轴的交点为简化中心，利用达朗贝尔原理分析是比较简单的.

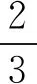
2.2 刚体平面运动惯性力系的简化

平面运动的刚体(平行于质量对称面)，运动可分解为随基点的平移和绕基点的转动，若简化中心取在质心，此时惯性力系向质心的简化得到的主矩与定轴转动中相似：MIC=-JCα.

例3 如图7所示，长l，质量为m的匀质杆AB,BD用铰链B连接，并用铰链A固定，位于图示平衡位置.今在D端作用一水平力F，求此瞬间两杆的角加速度.

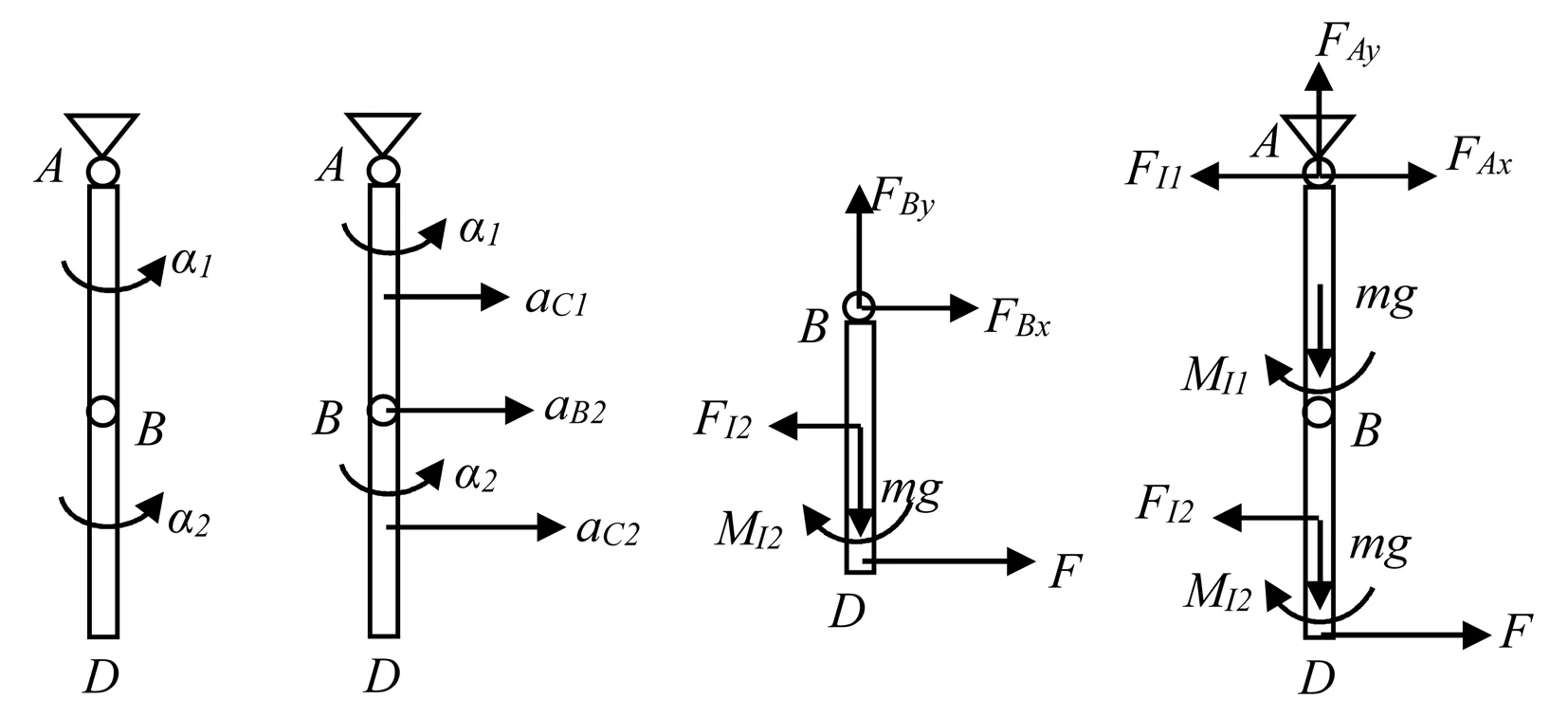
图7 图8 图9 图10

AB,BD两杆的运动情况如图8所示，AB杆做定轴转动，惯性力系简化中心取A点.BD杆做平面运动，惯性力系简化中心取质心C.

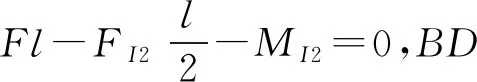
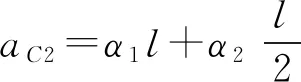
点评本题中既有定轴转动的杆AB，又有平面运动的杆BD，在计算惯性力系向简化点的主矩时，一定要注意简化中心的区别，AB杆的简化中心应该取在转轴位置的A点，BD杆的简化中心应取在质心，在计算两杆的转动惯量时会体现出区别.

惯性力的引入，对我们处理非惯性条件下动力学问题是很方便的，根据达朗贝尔原理，选择与质点无相对运动的坐标系，只要加上惯性力系，任何动力学问题都可以用静力学的方法来解决.刚体的惯性力系一般比较复杂，但对刚体做平移、定轴转动或平面运动，且垂直于转轴有质量对称面的情况，选择合适的简化中心，可以使惯性力系简化，一般建立主矢和主矩的三个平衡方程就可以解决问题.