应用转动定律分析质点和刚体组合的运动

鲁玉明

(上海大学理学院物理系 上海 200444)

大学物理是大学理工科类的一门基础课程，通过课程的学习，使学生熟悉自然界物质的结构、性质、相互作用及其运动的基本规律，为后续专业基础与专业课程的学习及进一步获取有关知识奠定必要的物理基础.

刚体是实际物体的一个理论模型，它不考虑物体的形变.大学物理一般用定轴转动定律分析刚体的定轴转动，而用质点运动定理分析质点的运动，在分析由质点和刚体混合体系运动过程时，就必须同时应用质点运动定理和刚体转动定律.质点是一种特殊的刚体，因此，同样可以用刚体的定轴转动定律来分析质点的运动.

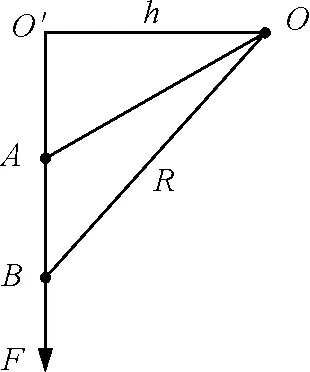
图1

如图1所示，一个质点在沿AB直线方向力F的作用下，从O点经过A点运动到B点，设转动轴处于O点并垂直于纸面.当质点处于O′时，分别应用质点运动定律

和质点转动定律

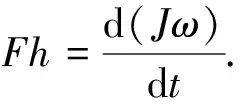
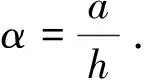
【例1】在图2所示装置中，物体的质量为m，圆柱状定滑轮质量为M，半径为R，质量均匀分布.设绳子长度不变，质量不计，绳与滑轮无相互滑动，滑轮光滑无摩擦.求圆柱体物体的角加速度.

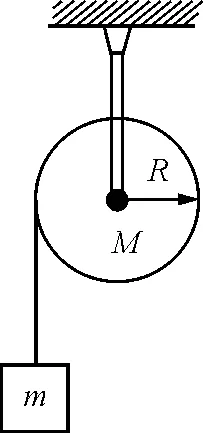
图2

解：设轴心为固定转动轴，则物体相对与转动轴的有效转动惯量为J′=mR2，系统受到的总力矩为mgR.根据转动定律有

解得

【例2】 在如图3所示装置中，物体的质量分别为m1和m2，且m1>m2.圆柱状定滑轮质量分别为M1和M2，半径为R1和R2，质量均匀分布.设绳子长度不变，质量不计，绳与滑轮无相互滑动，滑轮光滑无摩擦.试求两圆柱体的角加速度及它们之间绳的拉力.

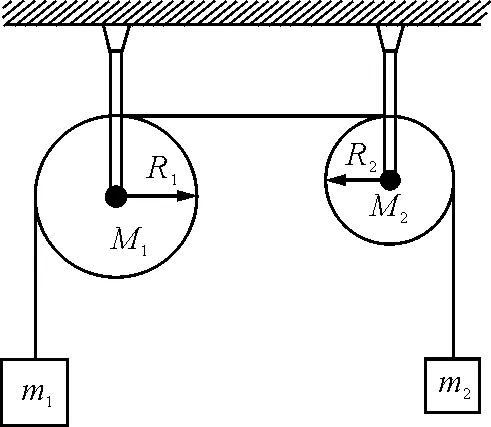
图3

解：设滑轮间拉力为T，因为m1，M1和m2，M2相对不同的转动轴运动，则需分别讨论之.对两个系统分别应用转动定律有

同时有

R1α1=R2α2

解之得

图4

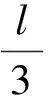
解：因为在碰撞过程中系统所受外力矩为零，可知系统角动量守恒为

解得

【例4】如图5所示，一根长为l，质量为M的均匀细木棒，竖立在无摩擦的水平桌面上.一个质量为m的小球，以速度为v0沿水平方向撞击木棒的一端.碰撞是完全弹性的.试求碰撞后小球的速度vq[4].

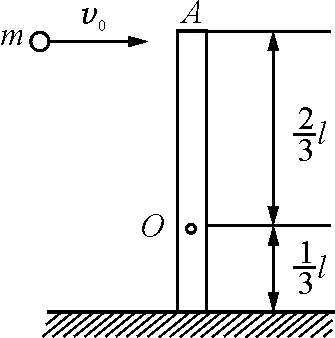
图5

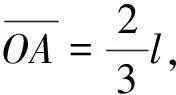
解得

通过以上例题分析可知，用刚体转动定律分析质点的运动，在某些情况下有很大的优势，在应用的过程中能加深学生对质点本质的理解，很适合介绍给学生.可以让学生掌握对物理分析中等效方法的使用，提高分析问题和解决问题的能力.

参考文献

1 张三慧.大学物理学(力学、热学)第三版.北京：清华大学出版社，2008

2 程守洙，江之永.普通物理学(1).北京：高等教育出版社，1998

3 石庆平，等.大学物理习题集.上海：上海大学出版社，2005.48

4 刘喜斌.用等效质点法求解刚体的平面运动.工科物理，1998，8(1):25～28