土体爆炸压密的原理及试验研究*

潘 强，张继春，郭学彬

（1.西南交通大学土木工程学院，四川 成都 610031；

2.西南科技大学环境与资源学院，四川 绵阳 621010）

土体爆炸压密的原理及试验研究*

潘 强1，张继春1，郭学彬2

（1.西南交通大学土木工程学院，四川 成都 610031；

2.西南科技大学环境与资源学院，四川 绵阳 621010）

针对目前土体爆炸压密理论研究不够深入、施工中主要依靠工程经验确定爆炸参数的现状，建立了基于塑性力学和爆炸力学的土体爆炸压密模型，推得压密效果（压密范围、压密程度）与爆炸参数之间的关系式，并通过室外试验进行验证。在孔径为48mm的炮孔中进行了不耦合系数分别为2.000、1.714、1.500、1.333、1.200、1.091和1.000的7组室外试验，通过测量爆炸前后的土体密度，进行理论和试验结果的对比分析。研究表明，不耦合装药时，压密效果的理论值随不耦合系数呈递增变化，而试验值呈先增后减的趋势，且在不耦合系数为约1.200时出现最大值；对于粘质粉土，压密效果较稳定，最大压密范围达到70cm，最大压缩比为1.055；给出的爆炸后土体压密计算公式的准确性较高，相对误差小于6.00%，可用于工程实际。

爆炸力学；压密原理；爆炸；土体密度

土体爆炸压密应用于软弱地基处理已有70多年的历史。尽管该方法具有省时、省料、经济效益和社会效益明显等优点，由于压密原理研究不足，确定爆炸参数主要依据工程经验，因而在实际工程中未得到广泛应用。土体爆炸压密研究于20世纪30年代在苏联发展起来，研究主要集中在饱和砂土在球形装药下的孔隙水压力、液化、沉降等方面，定性地分析其产生原因及发展规律［1－5］。随后开展了饱和砂土爆炸压密机理以及条形装药下压密效果的研究，但缺乏相应的理论指导及系统的建模分析［6－7］。孟祥跃等［8］、张均锋等［9－11］对饱和砂土在落锤式冲击荷载下的孔隙水压力、沉降等方面进行了较系统的研究，实验结果对爆炸压密土体有一定的指导意义。后来，爆炸压密越来越受到工程界的重视，屈俊童等［12－15］对条形装药下的爆炸压密做了较系统的研究，但也缺乏相应的理论建模分析。王仲琦等［16］、林大能等［17］对爆炸作用下粘土性状进行了数值模拟分析，观测爆炸后土体参数的变化，但未进行相应的试验验证；尽管在理论上对爆腔半径及塑性区半径进行了分析，但是采用的是Mises屈服准则，不能考虑静水压力对屈服的影响以及岩土材料在偏平面上拉压强度不等的特性。迄今为止，粘土和粉土爆炸压密理论与试验研究甚少，尤其是爆炸前后土体密度变化的规律尚不完全明确。

本文中，基于塑性力学和爆炸力学建立土体爆炸压密模型，分析爆炸压密作用机理，推导爆炸参数和压密效果之间的关系式，并以室外试验获得的土体密度曲线，计算压密范围和压密程度，探讨土体压密性状与爆炸参数之间的关系。

1 土体爆炸压密模型

考虑到土体在爆炸作用下产生塑性变形，运用塑性力学中反映岩土材料抗压强度大于抗拉强度效应以及对静水压力敏感性的Mohr-Coulomb屈服准则和爆炸力学中应力衰减规律理论推导塑性区范围，同时结合鲍姆方程推导塑性区压密程度及压密后土体密度的计算公式。

1.1 压密模型的建立

炸药在土体中爆炸时，爆轰气体绝热膨胀首先对周围土体产生持续时间极短的冲击压缩作用，在土体中激起冲击波，冲击波迅速向四周传播并衰减为应力波。随后爆生气体在空腔内准静态膨胀进一步压缩土体，当爆生气体的压力不足以推动土体压缩和应力波衰减到应力峰值小于土体产生径向位移所需应力时，爆炸压密作用消失，由此形成一定尺寸的爆炸空腔和压密区。此时，半无限土体可划分为空腔区、压密区和原状土区。

以柱状装药结构在土体中爆炸为例分析土体压密的原理。为突出重点、便于分析，假定：（1）装药结构空间断面为圆形，作用孔壁周围的压力均匀，形成的空腔和塑性区边界断面亦为圆形；（2）土体受爆炸压缩的响应时间比炸药爆轰时间长得多，考虑柱状药包全长范围内同时起爆；（3）土体为理想弹塑性材料，服从Mohr-Coulomb屈服准则；（4）试验区地应力（σ0＝γh）远小于爆炸应力，不考虑竖向地应力的影响（一般药柱埋深较浅）；（5）忽略柱状装药段的土体轴向位移，按照平面应变轴对称问题分析径向变形。

基于上述分析和假定，同时参考Vesic圆筒扩张理论［18］，简化后的土体爆炸压密模型如图1所示，图中的3个区域分别为空腔区（爆腔区）、塑性区（压密区）和弹性区（原状土区），r0表示炮孔半径，r1表示空腔半径，r2表示塑性区半径。

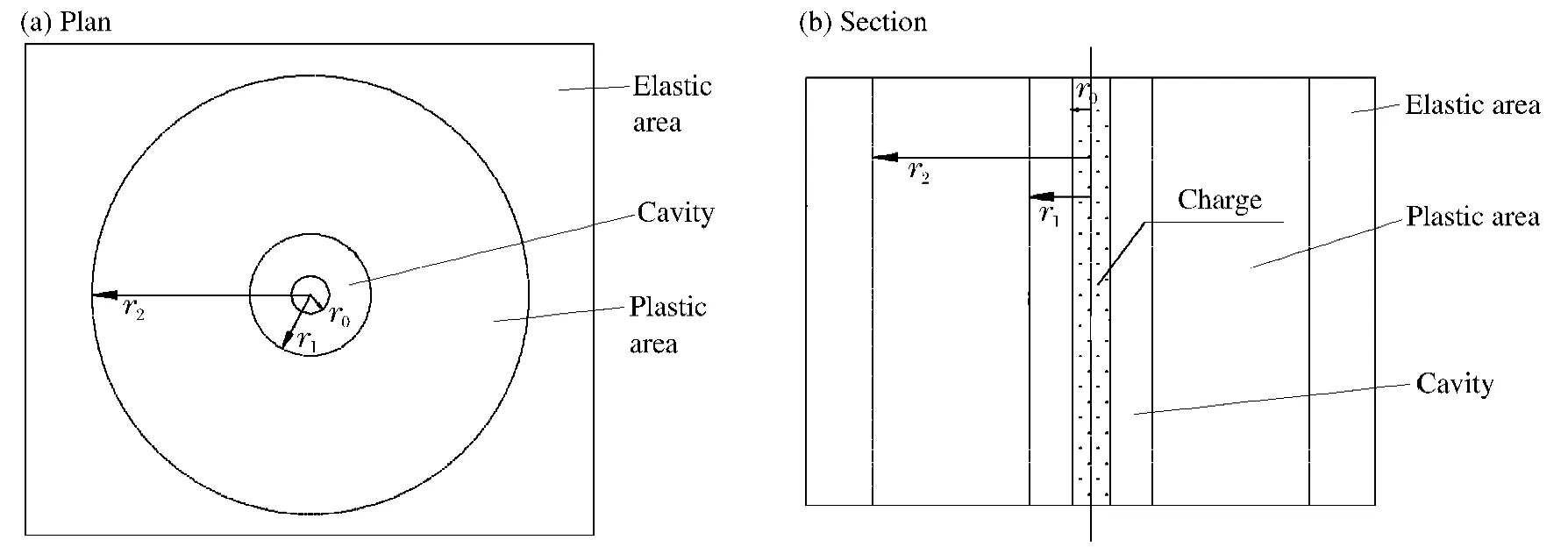
图1 土体爆炸压密模型Fig.1The explosion compaction model for soil material

1.2 塑性变形范围

考虑到土体为理想弹塑性材料，塑性区以外的弹性区土体变形在应力波衰减后逐渐恢复，所以塑性区的压缩量占主导地位，压密范围即塑性区域，定义压密范围等于塑性区半径r2减去空腔半径r1。根据土塑性力学理论，塑性区外无限大弹性区的应力场为［18］

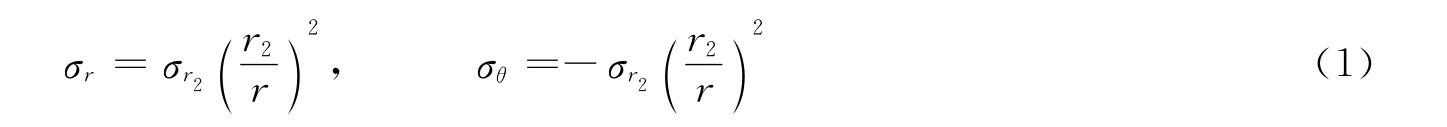
式中：σr为径向应力，σθ为切向应力，σr2为半径r2处的径向应力，r为爆心距。

当r＝r2时，根据应力边界连续性条件，塑性区外边界和弹性区内边界处的应力相等，且满足Mohr-Coulomb屈服准则

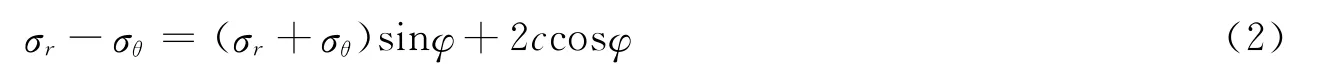
式中：c为土体粘聚力，φ为土体内摩擦角。

应力波在传播过程中其峰值应力可由下式给出

式中：σm为炮孔壁处初始峰值压力，为比例距离（＝r／r0，r0为炮孔半径），a为衰减指数，由于应力波在土体中的衰减比岩石中（应力波为2）快得多，所以试验中对粘质粉土而言a取值为3.5［19］。

爆炸压密过程中被压缩区域的介质遵循质量守恒定律

由式（1）～（4）可推得压密范围Δr的计算式

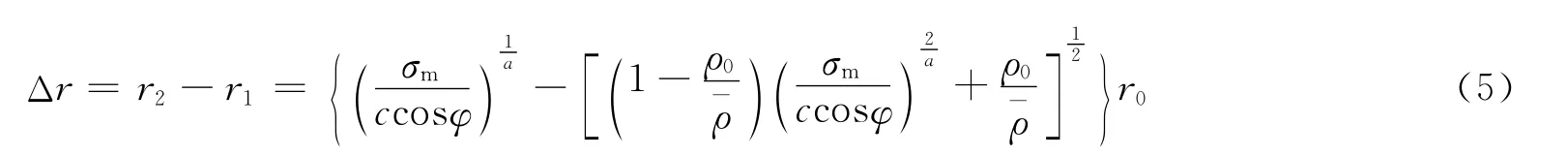
式中：σm为炮孔壁处初始峰值压力，炸药性能不变的条件下，σm由装药结构的耦合状态确定。

（1）当耦合装药时，炮孔壁处峰值压力为

式中：ρ0为土体初始密度，ρe为炸药密度，D为冲击波波速，De为炸药爆速。

由式（5）～（6）可推得耦合装药时的压密范围

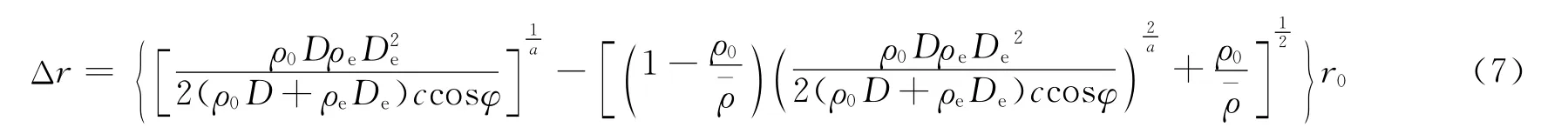
（2）当不耦合装药时，炮孔壁处峰值压力为

1.3 塑性变形程度分析

土体受到冲击波和爆生气体压缩后，密度发生变化。密度变化的程度用压缩比η表示，即η＝ρ／ρ0（ρ0、ρ分别为同一位置爆炸前后土体的密度）。根据爆炸力学中的鲍姆方程［20］，有

式中：K为不耦合系数，nb为爆轰产物撞击孔壁应力增强系数，一般取nb＝8～11［20］，对土体而言取8。

由式（5）、（8）可推得不耦合装药时的压密范围

式中：σr与炮孔壁处初始峰值压力有关，由于峰值压力σm的参数表达式与装药结构的耦合状态有关，下面同样对2种不同装药结构下爆炸后压缩比和土体密度分别表示。

（1）耦合装药时，爆炸后压缩比和土体密度表达式由式（3）、（6）、（10）推得

由式（11）及压缩比定义可得

由式（13）及压缩比定义可得

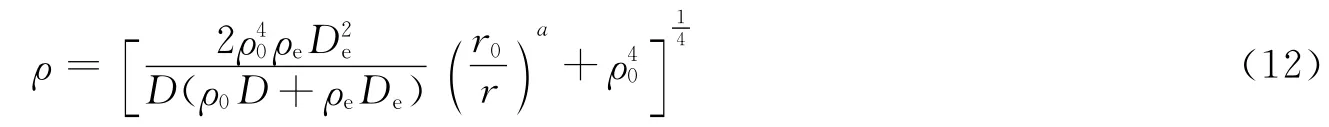
（2）不耦合装药时，爆炸后压缩比和土体密度表达式由式（3）、（8）、（10）推得

2 室外试验与分析

2.1 试验概况

试验场地周围空旷，地势平坦。表层松散土层约20cm、下层200cm的范围内为相对均质的粘质粉土，平均初始密度为1.85g／cm3，含水率为25%，粘聚力为5.5kPa，内摩擦角为8°。试验中采用密度为0.933g／cm3的2号岩石粉状硝铵炸药。为研究不同线装药密度条件下的土体爆炸压密性态，按照不同的不耦合系数进行7组爆炸压密试验，每组各进行2次试验。装药直径分别为24、28、32、36、40、44、48mm，装药长度为40cm。药卷固定于孔径为48mm、孔深度为100cm（除去表层松散覆盖土）的垂直炮孔中心，使用细颗粒粘土堵塞炮孔，堵塞长度为60cm，8号电雷管正向起爆。装药结构如图2所示。

图2 装药结构Fig.2 The charge structure

2.2 试验结果

2.2.1 爆腔状况

试验发现，只有直径de为24mm的药卷爆炸形成内部作用，地面出现鼓包。直径大于24mm的药卷爆炸形成外部作用，产生爆破漏斗。为观察爆炸后的爆腔（坑）形状、测量爆腔（坑）尺寸（列于表1中）以及布置取样点，所以采用人工开挖出取样断面。考虑到圆柱形药卷在半无限土体中的爆炸属于轴对称情况，为相互对比验证，沿炮孔中心呈90°开挖2个断面1-1和1-2，如图3所示。开挖长度为约120cm，深度为约150cm。

开挖完成后，观察2种爆破作用的断面发现，内部作用的爆腔由中间近似圆柱体和上下两端近似半球体组成；外部作用的爆坑由上部爆破漏斗、中间近似圆柱体和下部近似半椭球体组成，见图4。

图3 开挖后爆腔及测试断面照片Fig.3 The cavity and test section after the excavation

图4 爆炸空腔Fig.4 The explosion cavity

2.2.2 取样点布置

在测量爆炸后土体密度时，采用平均内径为30mm、平均高度为20mm的环刀在2个互相垂直的断面上进行取样，取样布置方式如图5所示。共布置3层取样点，第1层距离柱状爆腔顶10cm，各层之间间距为20cm（因爆腔壁产生破坏而使每层第1个取样点距爆腔壁7～10cm），每层共布置15个取样点，1～11个点之间的间距为5cm，11～15个点之间的间距为8cm。

图5 测试断面取样点照片Fig.5 Sampling points at the test section

2.2.3 密度曲线

每种药卷直径下均做2次试验相互验证，共得到4组测试数据。同一次试验呈90°的2个断面中，每层的2组测试数据进行算术平均并绘制密度曲线。结果发现，同一药卷直径下2次试验同一层数据具有相同的规律，同一次试验各层数据具有相近的规律；不同药卷直径下同一层数据也具有相近的规律。为了研究问题简便和说明变化趋势，选择各组爆炸压密试验同一次试验中的第2层测试数据曲线分析压密效果。

（1）沿爆源中心径向变化密度曲线。考虑到各组同一次试验第2层测试数据具有相同的规律，沿爆源中心径向变化的密度曲线选择直径分别为24、36mm的2种药卷测试数据进行曲线拟合获得试验曲线，如图6所示。从图中可以观察到压密范围、最大密度以及初始密度。

（2）爆心距相同处密度随药卷直径变化曲线。研究各组试验爆心距相同的位置，该点密度与药卷直径之间的变化规律。考虑到爆腔尺寸和压密范围，选择爆心距分别为50和70cm的2点绘制曲线，如图7所示。进行对比验证，说明变化趋势。

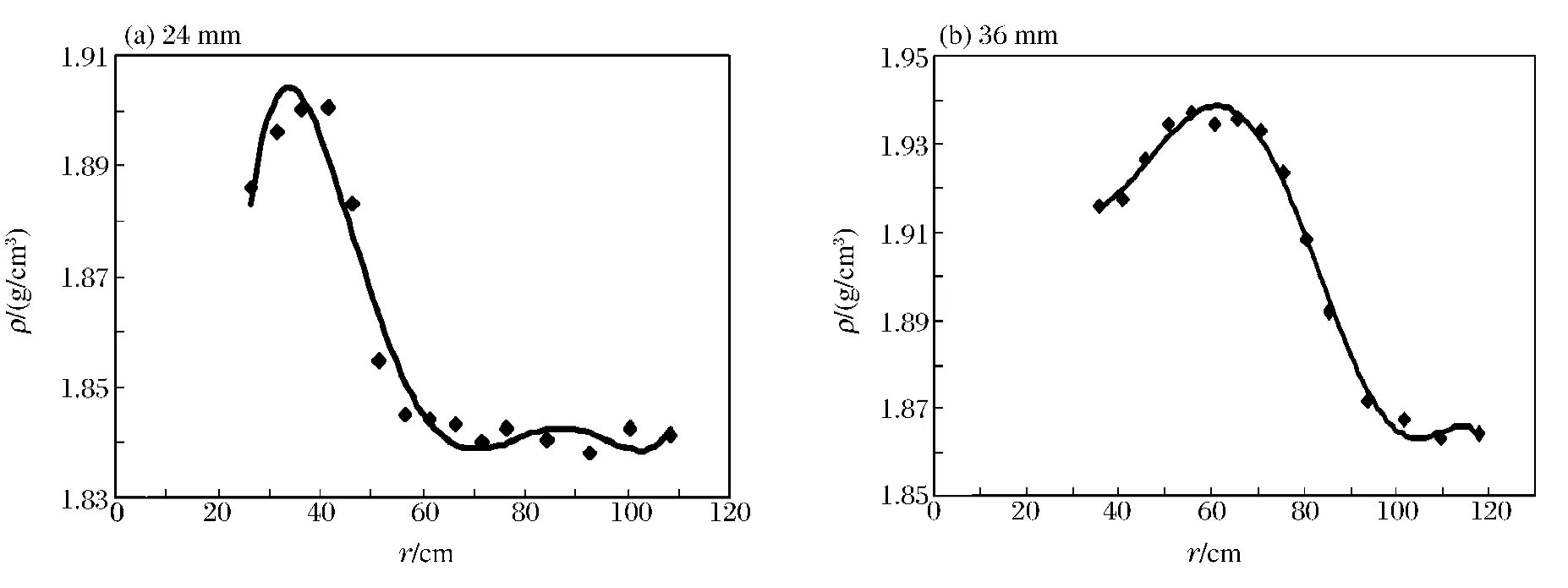
图6 药卷直径不同的情况下，土体密度沿爆源中心径向的变化Fig.6 Soil densities along with the radii of the explosion source in the cases of different cartridge diameters

图7 在爆心距不同的情况下，土体密度随药卷直径的变化Fig.7 Soil densities along with the cartridge diameters in the cases of different distances from the explosion source

2.3 结果计算与分析

从图6可以看出，密度随着爆心距的增大呈现先增大后减小的趋势，在爆腔壁处由于裂隙存在以及其径向延伸，造成密度值低于最大值，而大于初始密度值。随着径向距离的增加，裂隙变小直至延伸终止，土体密度增大。当超过一定距离时，爆炸能量已不能使土体压密，这时密度曲线递减至一近似水平线，接近初始密度值。从图7可以看出，在距离爆源中心某一点处，密度值随着药卷直径增大呈现先增大后减小的趋势，由于最佳压密效果取决于峰值压力和作用时间，峰值压力和作用时间相互制约，以致于曲线呈现先增大后减小的趋势，出现峰值。2处试验曲线在药卷直径为40mm左右密度值最大，即此装药条件下的压密程度最佳。

爆炸后土体压密效果参数可以由理论公式（7）、（9）、（11）～（14）和试验数据图6共同给出列于表1中，表中εΔr、εηmax和ερ－为相对误差，且相对误差＝（理论值－试验值）／试验值。

表1 在孔径为48mm时，土体压密效果参数的比较Table 1 Comparison of soil compaction parameters in the case of the 48-mm-diameter hole

（1）从表1可以看出，爆炸空腔平均半径随着药卷直径增大呈递增趋势，因为随着药卷直径增大，线装药密度增大，作用于土体的峰值压力增大。

（2）从表1理论和试验数据可以看出，不耦合系数从2.000减小至1.091时，压密范围、最大压缩比和平均密度的理论值呈递增变化；试验值呈先增后减变化且在不耦合系数为1.200时达到最大值。同时，耦合时压密参数值小于不耦合时最大压密参数值。

（3）产生上述规律的主要原因：不耦合时，三者的理论值仅与峰值压力有关，即与不耦合系数呈反比例关系；试验值与峰值压力和作用时间有关，是两者呈此消彼长关系综合作用的结果。另外，采用不耦合装药可以增大应力波的峰值压力及其作用时间。

（4）从表1相对误差数据可以看出，压密范围、最大压缩比和平均密度可以使用理论公式预测实际情况，误差不超过6.00%，仅当不耦合系数接近于1（小于1.100）时，需采用耦合装药理论公式预测，否则误差达30%左右。

（5）数据相对误差不超过6.00%，主要是试验和测量误差。另外，不耦合系数接近于1（小于1.100）时，考虑到炮孔、药卷变形以及药卷包装，实际中就相当于耦合装药，而理论值使用不耦合公式计算，以致于误差达30%左右。

3 结 论

（1）不同装药条件下的爆炸压密试验结果表明，粘质粉土爆炸压密的可重复性强，压密效果较稳定。同时，在孔径为48mm时，最大压密范围为70cm，最大压缩比为1.055。

（2）不耦合装药内部爆炸时，压密范围、最大压缩比和平均密度的理论值随不耦合系数呈递增变化，而三者的试验值呈先增后减的趋势且在不耦合系数为1.200左右出现最大值。即K＝1.200左右，压密范围和压密程度达到最佳。

（3）给出的土体爆炸压密计算公式的准确性较高，理论值与试验值接近，计算误差小于6%。

［1］Kummeneji O，Eide O.Investigation of loose sand deposits by blasting［C］∥Proceedings of the Fifth International Conference on Soil Mechanics and Foundation Engineering.Paris，1961：491-497.

［2］Prough B J.Densification of soils by explosive vibrations［J］.Journal of Construction Division，ASCE，1963，89（1）：79-100.

［3］Ivanov P L.Consolidation of saturated soils by explosions［C］∥Proceedings of the International Conference on Compaction，ENPC-LCPC.Paris，1980：331-337.

［4］Charlie W A，Jacobs P J，Doehring D O.Blast-induced liquefaction of an alluvial sand deposit［J］.Geotechnical Testing Journal，1992，15（1）：14-23.

［5］石教往，佟锦岳，熊长汉，等.爆炸压实饱和砂土的试验研究［J］.长江科学院院报，1992，9（4）：25-32.

SHI Jiao-wang，TONG Jin-yue，XIONG Chang-han，et al.An experimental research on compaction of saturated sand soil by explosion［J］.Journal of Yangtze River Scientific Institute，1992，9（4）：25-32.

［6］黄承贤.土中爆扩及其挤密效应的研究［J］.爆炸与冲击，1996，16（4）：354-360.

HUANG Cheng-xian.Study of blast-enlargement and compaction in soil［J］.Explosion and Shock Waves，1996，16（4）：354-360.

［7］杨年华.成孔爆破法处理地基技术介绍［J］.爆破，1997，14（1）：61-65.

［8］孟祥跃，张均锋，俞善炳，等.冲击载荷下饱和砂土中孔隙水压力的变化及其与液化密实的关系［J］.岩土工程学报，1999，21（3）：7-11.

MENG Xiang－yue，ZHANG Jun-feng，YU Shan-bing，et al.The variation of porewater pressure and its relationship with liquefaction and densification in saturated sand under impact loading［J］.Chinese Journal of Geotechnical Engineering，1999，21（3）：7-11.

［9］张均锋，孟祥跃，谈庆明，等.冲击载荷下饱和砂土密实与排水过程的初步分析［J］.岩石力学与工程学报，2000，19（5）：622-625.

ZHANG Jun-feng，MENG Xiang－yue，TAN Qing-ming，et al.Primary analysis on process of densification and drainage of saturated sand under impact loading［J］.Chinese Journal of Rock Mechanics and Engineering，2000，19（5）：622-625.

［10］张均锋，孟祥跃，谈庆明，等.冲击载荷下饱和砂土砂面沉降的试验研究［J］.岩石力学与工程学报，2001，20（4）：519-523.

ZHANG Jun-feng，MENG Xiang－yue，TAN Qing-ming，et al.Laboratory study on the settlement of sand surface of saturated sand under impact loading［J］.Chinese Journal of Rock Mechanics and Engineering，2001，20（4）：519-523.

［11］张均锋，孟祥跃.冲击载荷下饱和砂土中超孔隙水压力的建立与消散过程［J］.岩石力学与工程学报，2003，22（9）：1463-1468.

ZHANG Jun-feng，MENG Xiang－yue.Build-up and dissipation of excess pore water pressure in saturated sand under impact loading［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22（9）：1463-1468.

［12］屈俊童，周健，吴晓峰.爆炸法密实砂土地基（Ⅰ）：研究现状［J］.工程爆破，2006，12（3）：14-17.

QU Jun-tong，ZHOU Jian，WU Xiao-feng.Explosive compaction of sand ground foundation（Ⅰ）：Review［J］.Engineering Blasting，2006，12（3）：14-17.

［13］屈俊童，周健，吴晓峰.爆炸法密实砂土地基（Ⅱ）：现场试验［J］.工程爆破，2006，12（4）：4-8.

QU Jun-tong，ZHOU Jian，WU Xiao-feng.Explosive compaction of sand foundation（Ⅱ）：In-situ trials［J］.Engineering Blasting，2006，12（4）：4-8.

［14］屈俊童，周健，吴晓峰.爆炸法密实砂土地基（Ⅲ）：模型试验［J］.工程爆破，2007，13（1）：1-5.

QU Jun-tong，ZHOU Jian，WU Xiao-feng.Explosive compaction of sand foundation（Ⅲ）：Laboratory test［J］.Engineering Blasting，2007，13（1）：1-5.

［15］屈俊童，周健，吴晓峰.爆炸法密实砂土地基（Ⅳ）：设计方法［J］.工程爆破，2007，13（2）：1-6.

QU Jun-tong，ZHOU Jian，WU Xiao-feng.Explosive compaction of sand foundation（Ⅳ）：Design method［J］.Engineering Blasting，2007，13（2）：1-6.

［16］王仲琦，张奇，白春华.爆炸挤压粘土密度变化过程的数值模拟［J］.岩土工程学报，2001，23（3）：350-353.

WANG Zhong－qi，ZHANG Qi，BAI Chun-hua.Numerical simulation on variation of density of the soil compacted by explosion［J］.Chinese Journal of Geotechnical Engineering，2001，23（3）：350-353.

［17］林大能，胡伟，彭刚.岩土介质爆炸挤压特性分析［J］.岩石力学与工程学报，2003，22（11）：1767-1770.

LIN Da-neng，HU Wei，PENG Gang.Analysis on blasting extrusion characteristic of soil and rock［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22（11）：1767-1770.

［18］龚晓南.土塑性力学［M］.杭州：浙江大学出版社，1999：251-253.

［19］哈努卡耶夫.矿岩爆破物理过程［M］.刘殿中，译.北京：冶金工业出版社，1980：60.

［20］戴俊.爆破工程［M］.北京：机械工业出版社，2005：109-113.

The principle of soil compaction by explosion and its experimental investigation＊

PAN Qiang1，ZHANG Ji-chun1，GUO Xue-bin2
（1.School of Civi1 Engineering，Southwest Jiaotong University，Chengdu 610031，Sichuan，China；
2.School of Environment and Resources，Southwest University of Science and Technology，Mianyang 621010，Sichuan，China）

Aimed at the status of explosion compaction，which was not thorough in theory study and relied mainly on engineering experience to determine blast parameters in constructions，a soil explosion compaction model was developed which was based on plastic mechanics and mechanics of explosion.The relations between compaction effects（compaction range，compaction degree）and explosive parameters were derived and verified by the field tests.The seven field tests were carried out in the holes with the diameter of 48mm and the corresponding non-coupling coefficients were 2.000，1.714，1.500，1.333，1.200，1.091and 1.000，respectively.And theoretical calculations and field test results were compared by measuring the soil density before and after the explosion.Investigated results indicate that in the case of non-coupling charge，the theoretical value of compaction effect increases with the increase of non-coupling coefficient，while the experimental data first increases and then decreases，arriving at the maximum for the non-coupling coefficient of around 1.200.For the clayey silt，the compaction effect was more stable，the largest compaction range attains 70cm and the maximum compression ratio is 1.055.The developed soil compaction formulas after explosion are more accurate and the relative error is less than 6.00%，so that these formulas can be applied to engineering practice.

mechanics of explosion；compaction principle；explosion；soil density

30January 2010；Revised 16April 2010

ZHANG Ji-chun，jczhang2004＠126.com

（责任编辑 张凌云）

O389；TU472.1 国标学科代码：130·3599

A

1001-1455（2011）02-0165-08＊

2010-01-30；

2010-04-16

潘 强（1985— ），男，硕士研究生。