非对称质量磨蚀导致正侵彻弹体的弯曲屈服*

赵 军，陈小伟，金丰年，徐 迎

（1.解放军理工大学工程兵工程学院，江苏 南京 210007；

2.中国工程物理研究院总体工程研究所，四川 绵阳 621900）

非对称质量磨蚀导致正侵彻弹体的弯曲屈服*

赵 军1，陈小伟2，金丰年1，徐 迎1

（1.解放军理工大学工程兵工程学院，江苏 南京 210007；

2.中国工程物理研究院总体工程研究所，四川 绵阳 621900）

给出了在一定的非对称质量磨蚀条件下垂直于弹体侵彻方向的横向荷载，并结合考虑质量磨蚀的弹体轴向阻力计算方法，得到了正侵彻弹体在压弯联合作用下的屈服分析方法。讨论了影响弹体由于非对称质量磨蚀而弯曲屈服的主要因素。分析表明，弹体的危险截面在承受较大的轴向荷载时，对由非对称质量磨蚀导致的横向荷载极为敏感。

爆炸力学；弯曲；非对称质量磨蚀；正侵彻弹体；屈服；混凝土靶

深钻地武器是打击敌方重要的地下坚固军事目标，如地下掩体、地下指挥所、地下发射基地的有效武器。其作用效应是指弹体深层侵彻地下目标而保持结构不损坏，战斗部在预定深度爆炸，摧毁深层目标。然而，深钻地武器在侵彻过程中可能面临弹体结构稳定性问题，即在撞击初期和侵彻过程中弹体结构的动态屈曲、弯曲、断裂以及由于弹体不均匀受力而导致的弹道偏转失稳。相关问题与弹体的初始撞击速度、方向、弹靶材料性质和其他偶然因素有关。随着研究重点由常规弹速（侵彻速度＜0.9km／s）向高速侵彻（1.0km／s＜侵彻速度＜1.5km／s）的转移，弹体结构稳定性问题（尤其是弯曲、断裂模式）已经成为关注热点。

实验结果表明，一些随机因素（弹体头部非对称磨蚀、靶材不均匀等）是引起正侵彻弹体产生横向干扰，导致弹体偏转失稳（甚至弯曲和断裂），从而导致弹体失去侵彻能力的主要原因，并且这种影响在侵彻速度越高时反映越明显。M.J.Forrestal等［1］、D.J.Frew 等［2］完成了6组不同曲径比ψ＝s／d的尖卵形弹以1.3～1.7km／s侵彻不同强度混凝土靶的实验，观察到由于弹体头部发生明显不对称磨蚀而导致的弹体严重弯曲和断裂现象。杨建超等［3］进行了不同条件下弹体高速侵彻（0.8～1.5km／s）混凝土靶的实验，研究高速撞击条件下弹体的侵彻能力、弹体磨蚀和破坏等问题，也观察到弹体发生严重弯曲而导致弹体侵彻能力降低的现象。X.W.Chen等［4］、L.L.He等［5］、陈小伟等［6］、赵军等［7］根据 M.J.Forrestal等［1］、D.J.Frew等［2］的实验结果，讨论了影响弹体质量磨蚀的主要因素，给出了考虑弹头部质量磨蚀的侵彻阻力计算方法，但只针对轴对称质量磨蚀条件。

本文中，将研究非对称质量磨蚀对正侵彻弹体弯曲的影响。应用弹体侵彻混凝土靶的法向膨胀理论，给出在一定的非对称质量磨蚀条件下垂直于弹体侵彻方向的横向荷载，并结合能够反映弹头形状因子连续变化的弹体轴向阻力计算方法，得到由于非对称质量磨蚀而导致正侵彻弹体在压弯联合作用下的屈服分析方法。

1 弹体轴向阻力计算

侵彻实验研究表明，刚性弹侵彻半无限混凝土靶将形成锥形弹坑和隧道区。对于质量为m、弹径为d的刚性弹以初速度v0正侵彻密度及无侧限抗压强度分别为ρt和fc的混凝土靶的工况，弹体在混凝土靶中锥形弹坑和隧道区所受轴向阻力分别为［8－9］

式中：c为常数，可由k′d处的连续条件得出；R为与混凝土靶无侧限抗压强度fc和弹靶尺度有关的静阻力项；v为弹体瞬时侵彻速度；N＊为量纲一弹头形状因子，对于尖卵形弹头，有

式中：k为经验常数，在弹体初始速度为v0时，弹头形状因子为；侵彻终止时，残余弹头形状因子为。将式（3）代入式（1）就可得出在侵彻过程中能够反映头形变化的轴向阻力。

需指出的是，当弹体头部发生轴对称质量磨蚀时，弹体只承受轴向力作用；当弹体头部发生非对称的质量磨蚀时，弹体在承受轴向力的同时，还要承受垂直于弹体侵彻方向的横向作用力。

弹体头部的质量磨蚀对于弹体侵彻阻力具有不可忽略的影响，弹头因为磨蚀而不断钝粗，即弹头形状因子N＊逐渐增大。弹头形状因子在整个侵彻过程中是依赖于时间的函数。赵军等［7］假设侵彻过程中弹头形状因子与初始弹头形状因子保持瞬时速度平方的线性关系，用以描述弹头形状因子的变化

2 弹体横向作用力分析

考虑弹体正侵彻半无限靶的情况，弹头纵、横截面如图1所示。这里假设经过非对称质量磨蚀后弹头形成具有不同曲径比的2个半侧，见图1（b）。为了保证弹头部的连续性，令过渡处光滑连接。对于横向力而言，在靠近过渡处位置的法向应力分量很小，对积分结果的影响几乎可以忽略不计，因此该假设既可方便弹体受力分析又能较真实地反映实际情况。弹头长度为h，弹头母线函数y＝y（x），y（0）＝d／2，y（h）＝0。

按对称性分析1／4弹头横截面，不计摩擦力作用，只考虑作用在弹头上的法向正应力，则作用在弹头上并且垂直于弹体侵彻速度方向的横向力增量为

图1 侵彻弹体头形纵、横截面示意图Fig.1Cross sections of a projectile nose

将式（5）代入式（4）就可以得到

积分式（6）可得作用在弹头一侧的横向作用力

根据动态空腔膨胀理论，σn＝R＋＝R＋ρtv2cos2θ，可以得到该式与弹体所受轴向作用力式（1）相似，仅量纲一形状因子Na和Nb不同

对于尖卵形弹头来说

由于弹头两侧存在不同的曲径比，就致使弹头两侧受力不均，因此弹头两侧所受横向作用力之差即为弹体头部所受的横向作用力

3 压弯联合作用下的弹体受弯分析

先前关于弹头质量磨蚀对弹体受力变化的分析［7，10－11］都是基于弹头部发生对称的质量磨蚀，此时弹体只受轴向力作用，不受横向力作用。但通常弹体在高速侵彻过程中，由于靶体材料的不均匀性，弹头部极易发生非对称质量磨蚀，导致弹体在承受较大轴向作用力的同时也承受垂直于侵彻速度方向的横向力作用，而这种横向作用力的存在会导致弹体发生弹道偏转甚至弯曲破坏。

皮爱国等［12］基于刚塑性自由梁在横向冲击载荷下的动力学响应研究方法，得到了梁内任一截面在横向荷载下的剪力和弯矩分布规律，并给出了在轴力和弯矩载荷共同作用下梁截面的屈服条件。从弹体的使用性能出发，使用弹性屈服极限函数更符合实际和偏安全的考虑。对于在弹性范围内承受轴力N和弯矩载荷M 共同作用梁截面的屈服函数及屈服条件为

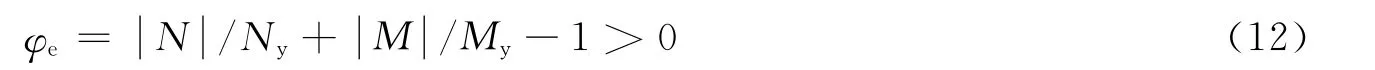
式中：Ny和My分别为截面单纯受压和单纯受弯的屈服极限。

陈小伟［13］给出了沿弹体轴线方向距弹体头部x距离的截面上的等效载荷分布

式中：l理论上为弹体头部荷载等效作用点至弹体后端的长度，为简化，近似认为l为弹体全长。

基于上述理论，便可对在高速侵彻过程中弹体在压弯联合作用下的受弯状态进行分析。弹体的质量磨蚀是伴随着整个侵彻过程不断增加的，实质上观察到的弹体非对称质量磨蚀是在侵彻过程结束之后。这里假设当弹体所受轴向阻力达到最大值时，弹头部的非对称质量磨蚀差异就已经达到最大，即此时弹头两侧的曲径比差异达到最大，这应是对弹体不利的受力状态的最保守估计。

根据式（1）和式（3）所给出的弹体侵彻过程中轴向阻力的变化形式，对于给定的初始撞击速度v0，轴向阻力Fa是关于v2的二次函数，经求导∂Fa／∂（v2）＝0可得

正常磨蚀条件下弹头形状因子的变化可依据式（3）来得到。根据本文中所做假定，令其中一侧弹头形状因子变化形式如式（3），当弹体所受轴向阻力达到最大值时，＝，弹头曲径比为ψ1；而另外一侧弹头磨蚀情况更严重，弹头形状因子为，弹头曲径比为ψ2。这样，将两侧弹头所受轴向阻力相加平均即可得到作用在弹体头部的轴向力为

将式（16）和式（11）分别代入式（13），最终合并到式（12）可得

式中：σy为弹体材料屈服强度。圆筒形装药弹体截面的相关参数可类似得到。

对于一定的非对称质量磨蚀差异，通过对式（17）求导dφe／dx＝0可得屈服函数最大值所在截面

对于实心弹体截面，有

将式（14）及式（18）代入式（17）整理后可得在一定弹体几何下，以初始速度v0侵彻给定靶体，沿弹长方向屈服函数与非对称质量磨蚀之间的关系

式中：λ1为弹体长细比，λ1＝l／d。将式（19）代入式（20）可得在非对称质量磨蚀条件下弹体最危险截面屈服函数值，从而可根据屈服条件对弹体是否受弯进行判断。

4 屈服函数的参数相关性

从式（20）可以看出，屈服函数φe与沿弹长位置x／l，弹体长细比λ1，初始弹头形状因子N＊i，弹体初始撞击速度v0，弹体材料强度σy，非对称质量磨蚀后的量纲一弹头形状参数Nae、Nbe、N＊e，表征靶体静阻力项的R，靶体密度ρt及经验常数k有关。在最大轴向阻力时，靶体静阻力项R为与混凝土靶无侧限抗压强度fc有关的量［8，14］，初始弹头形状因子N＊i为与初始弹头曲径比ψ有关的量，量纲一弹头形状参数Nae、Nbe、N＊e为与磨蚀后弹头两侧曲径比ψ1和ψ2有关的量，后者又与经验参数kv20相关，而弹体最危险截面可完全由式（19）确定。因此，弹体最危险截面在最大轴向阻力时屈服函数φm，e的参数相关性可进一步量纲一化为

式（21）列出了影响屈服函数的弹靶初始条件及非对称质量磨蚀条件。一般而言，对于深层侵彻弹体，弹形（即弹体长细比λ1和曲径比ψ）、弹材强度σy和混凝土密度ρt比较固定，可选择性较小。因此，下面仅对另外的2个初始条件，即混凝土靶无侧限抗压强度fc和弹体初始撞击速度v0，以及非对称质量磨蚀程度（ψ1－ψ2）对屈服函数的影响加以讨论。

4.1 屈服函数的参数影响

假设一初始弹头曲径比ψ＝3，长径比λ1＝10的弹体垂直侵彻半无限混凝土靶，取弹体材料σy＝1.5GPa，混凝土密度ρt＝2.3t／m3。

根据式（15）及式（2）可以得到在不同强度混凝土靶条件或在不同初始撞击速度条件下，弹体所受轴向阻力达到最大值时的弹头曲径比。赵军等［7］分析表明，混凝土靶无侧限抗压强度或初始撞击速度越高，弹体所受轴向阻力达到最大值时的剩余弹头曲径比越小，弹体质量磨蚀越严重。若同时给定弹体初始撞击速度及混凝土靶无侧限抗压强度，例如v0＝1.3km／s，fc＝50MPa，可知剩余弹头磨蚀一侧的曲径比ψ1＝1.05。下面对非对称质量磨蚀差异程度对弹体的量纲一轴向应力和弯曲应力及屈服函数的影响进行分析，如图2所示。由于非对称质量磨蚀是一种不确定性因素，现假设弹体在侵彻过程中发生3种不同程度的非对称质量磨蚀，即ψ2＝0.85，0.75，0.65。

图2 非对称质量磨蚀下量纲一轴向应力、弯曲应力和屈服函数沿弹长分布Fig.2 Dimensionless axial stress，bending stress and yielding function distribution along the projectile axis in the case of asymmetrical nose erosion

由图2可知，量纲一轴向压应力增加幅度很小，甚至可以忽略，表明不同程度的非对称质量磨蚀对量纲一弹头形状因子N＊e的变化影响很小；相反，非对称质量磨蚀对弹体的量纲一弯曲应力有显著影响，其值随非对称质量磨蚀的增大而迅速增加，在量纲一屈服函数中所占比例也显著增大。这说明高速侵彻弹体在承受较大的轴向荷载时，对由非对称质量磨蚀导致的横向荷载极敏感。从图2（b）中可以看出，随着非对称质量磨蚀差异的增大，危险截面逐渐由弧柱交接面向x＝l／3处靠拢。

4.2 非对称质量磨蚀的讨论

弹体以相同初始速度侵彻不同强度的混凝土靶或弹体以不同的初始速度侵彻相同强度的混凝土靶时，弹体最危险截面满足屈服条件时的非对称质量磨蚀差异，如图3所示。

图3 非对称质量磨蚀的差异随不同情况的变化Fig.3 Variation of asymmetrical nose erosion with different cases

从图3（a）中可以看出，在混凝土靶无侧限抗压强度提高相同的幅度下，非对称质量磨蚀差异降低幅度逐渐变小，说明当混凝土靶无侧限抗压强度增大到一定程度时，对弹体受弯影响不明显。这里未考虑混凝土骨料大小及硬度影响，假设k值仅随混凝土靶无侧限抗压强度变化。从图3（b）可以看出，对于侵彻相同无侧限抗压强度的混凝土靶体来说，非对称质量磨蚀差异随弹体初始撞击速度几乎成线性降低。图3表明，在较高混凝土靶无侧限抗压强度和撞击速度时，较小的的非对称质量磨蚀也可导致弹体弯曲屈服。以上分析，有利于在不同初始撞击速度下，对弹体最危险截面满足屈服条件时的非对称质量磨蚀差异加以判断。

进一步，如果弹体在不同的初始撞击速度下均发生相同程度的非对称质量磨蚀差异，即非对称质量磨蚀差异程度及混凝土靶体无侧限抗压强度一定的条件下，例如ψ1－ψ2＝0.3，fc＝50MPa，就可以分析弹体初始撞击速度对屈服函数产生的影响，如图4所示。可知，随着初始撞击速度的提高，屈服函数增幅加大，表明在高速侵彻时，初始撞击速度的提高，对弹体发生受弯屈服的危害增大。

图4 非对称质量磨蚀程度相同时量纲一屈服函数随初始撞击速度的变化Fig.4 Dimensionless yielding function distribution along the projectile axis at different impact velocities

5 实验数据分析

图5 非对称的质量磨蚀后不同曲径比的弹头的几何形状Fig.5 Asymmetrical projectile noses of different caliber-radius-head projectiles after mass abrasion

M.J.Forrestal等［1］、D.J.Frew等［2］在弹体侵彻混凝土靶的实验研究中分别观察到显著的质量磨蚀现象，并且在高速侵彻阶段观察到了较明显的非对称质量磨蚀导致的弹体发生弯曲和断裂现象。X.W.Chen等［4］通过对 M.J.Forrestal 等［1］、D.J.Frew等［2］实验后的弹形进行几何逼近，寻找到了最接近的尖卵形包络，近似按对称的质量磨蚀形式给出了实验后弹体头部的曲径比。将磨蚀后的弹头实际几何形状与该几何包络相比较，能看出较明显的非对称质量磨蚀，如图5所示。

结合上述理论工作，针对实验［1－2］进行分析，讨论在不同工况下弹体最危险截面满足屈服条件时弹头部须达到的非对称质量磨蚀差异。根据不同的实验工况，可先给出弹体所受轴向阻力达到最大值时的剩余弹头一侧曲径比ψ1的值，再根据式（20）即可得出当非对称质量磨蚀差异达到何种程度时，弹体有受弯屈服的危险，并与实验结果相对照。图6给出了一定的初始撞击速度下弹体所受轴向阻力达到最大值时的其中一侧的弹头曲径比和弹体发生弯曲破坏所要求的弹头不对称磨蚀程度［1－2］。图中相关弹靶参数可参见文献［4］。

从实验结果［1－2］可知，弹体高速侵彻强度为19.5MPa的混凝土靶时，当弹体初速超过1.3km／s时弹体发生严重的偏航现象，并从靶体侧向飞出；当弹体初速超过1.4km／s时，弹体发生严重的弯曲现象而导致侵彻深度严重降低；当弹体初速超过1.6km／s时，弹体发生断裂。侵彻强度为51.0MPa的混凝土靶实验中，当弹体初速超过1.3km／s时弹体发生严重的偏航现象；而侵彻强度为62.8MPa的混凝土靶实验中，当弹体初速超过1.2km／s时弹体就已经发生断裂。

由实验工况分析，进一步佐证了混凝土靶无侧限抗压强度和弹体初始撞击速度对于弹体发生受弯屈服时所需的非对称质量磨蚀程度的影响。在相同的初始撞击速度下，混凝土靶无侧限抗压强度越高，所需的非对称质量磨蚀程度越小，弹体越容易受弯屈服。而对于同种无侧限抗压强度的混凝土靶体来说，初始撞击速度越高，弹体发生受弯屈服所需的非对称质量磨蚀程度也越小。另外，其他一些能够对弹体质量磨蚀产生影响的因素（如混凝土骨料硬度）对于弹体发生弯曲破坏时所需要的非对称质量磨蚀程度也有影响，骨料硬度越高，所需的非对称质量磨蚀差异程度越小。

图6 Sandia侵彻实验数据理论分析Fig.6 Theoretical analysis on Sandia’s penetration experimental data

6 结 论

发生在弹体头部的非对称质量磨蚀是弹体高速正侵彻混凝土靶时发生偏航、弯曲甚至断裂的重要原因之一。给出了由于非对称质量磨蚀而导致弹体承受垂直于侵彻速度方向的横向作用力的工程计算方法，可对不同非对称质量磨蚀程度下弹体所受横向作用力进行预估。非对称质量磨蚀而导致弹体在压弯荷载联合作用下的最危险截面处于弧柱交接面和弹体全长的1／3之间。弹体在承受较大的轴向荷载时，对由非对称质量磨蚀导致的横向荷载很敏感。影响弹体质量磨蚀程度的主要因素，如弹体初始撞击速度、混凝土靶无侧限抗压强度和混凝土骨料硬度仍是影响弹体由于非对称质量磨蚀而弯曲屈服的重要因素。然而正侵彻弹体弯曲问题较复杂，不仅是由于弹体头部发生非对称的质量磨蚀，还可能是混凝土靶材的不均匀性而导致弹体受力不均激发，以及弹体轴向屈服或屈曲的后效等。

［1］Forrestal M J，Frew D J，Hanchak S J，et al.Penetration of grout and concrete targets with ogive-nose steel projectiles［J］.International Journal of Impact Engineering，1996，18（5）：465-476.

［2］Frew D J，Hanchak S J，Green M L，et al.Penetration of concrete targets with ogive-nose steel rods［J］.International Journal of Impact Engineering，1998，21（6）：489-497.

［3］杨建超，何翔，金栋梁.弹体高速侵彻混凝土质量侵蚀特性试验研究［J］.防护工程，2010，32（1）：6-10.

YANG Jian-chao，HE Xiang，JIN Dong-liang.Experimental investigation into mass loss of projectiles that penetrate concrete target at high velocity［J］.Protective Engineering，2010，32（1）：6-10.

［4］Chen X W，He L L，Yang S Q.Modeling on mass abrasion of kinetic energy penetrator［J］.European Journal of Mechanics：A／Solids，2010，29（1）：7-17.

［5］He L L，Chen X W，He X.Parametric study on mass loss of penetrators［J］.Acta Mechanica Sinica，2010，26（4）：585-597.

［6］陈小伟，杨世全，何丽灵.动能侵彻弹体的质量侵蚀模型分析［J］.力学学报，2009，41（5）：752-760.

CHEN Xiao-wei，YANG Shi-quan，HE Li-ling.Modeling on mass abrasion of kinetic energy penetrator［J］.Chinese Journal of Theoretical and Applied Mechanics，2009，41（5）：752-760.

［7］赵军，陈小伟，金丰年，等.考虑头形磨损变化的动能弹极限侵彻深度研究［J］.力学学报，2010，42（2）：212-218.

ZHAO Jun，CHEN Xiao-wei，JIN Feng-nian，et al.Studying on penetration depth limit of kinetic energy penetrator with including the effect of mass abrasion［J］.Chinese Journal of Theoretical and Applied Mechanics，2010，42（2）：212-218.

［8］Forrestal M J，Altman B S，Cargile J D，et al.An empirical equation for penetration depth of ogive-nose projectiles into concrete targets［J］.International Journal of Impact Engineering，1994，15（4）：395-405.

［9］Forrestal M J，Frew D J，Hickerson J P，et al.Penetration of concrete targets with deceleration-time measurements［J］.International Journal of Impact Engineering，2003，28（5）：479-497.

［10］Jones S E，Hughes M L，Toness O A，et al.A one-dimensional analysis of rigid-body penetration with high-speed friction［J］.Proceedings of the Institution of Mechanical Engineers：Part C：Journal of Mechanical Engineering Science，2003，217（4）：411-422.

［11］Davis R N，Neely A M，Jones S E.Mass loss and blunting during high-speed penetration［J］.Proceedings of the Institution of Mechanical Engineers：Part C：Journal of Mechanical Engineering Science，2004，218（9）：1053-1062.

［12］皮爱国，黄风雷.大长细比弹体斜侵彻混凝土靶的动力学响应［J］.爆炸与冲击，2007，27（4）：331-338.

PI Ai-guo，HUANG Feng-lei.Dynamic behavior of a slender projectile on oblique penetrating into concrete target［J］.Explosion and Shock Waves，2007，27（4）：331-338.

［13］陈小伟.动能深侵彻弹的力学设计（I）：侵彻／穿甲理论和弹体壁厚分析［J］.爆炸与冲击，2005，25（6）：499-505.

CHEN Xiao-wei.Mechanics of structural design of EPW（I）：The penetration／perforation theory and the analysis on the cartridge of projectil［J］.Explosion and Shock Waves，2005，25（6）：499-505.

［14］Li Q M，Chen X W.Dimensionless formulae for penetration depth of concrete target impacted by a non-deformable projectile［J］.International Journal of Impact Engineering，2003，28（1）：93-116.

Bending of normal penetrating projectiles induced by asymmetrical mass abrasion＊

ZHAO Jun1，CHEN Xiao-wei2，JIN Feng-nian1，XU Ying1
（1.Engineering Institute of Engineering Corps，PLA University of Science and Technology，Nanjing 210007，Jiangsu，China；
2.Institute of Structural Mechanics，China Academy of Engineering Physics，Mianyang 621900，Sichuan，China）

Asymmetrical mass abrasion is one of the dominant reasons to cause a projectile bending，yawing and break when it strikes a concrete target normally at high velocity.The spherical cavity-expansion model is employed to construct the transverse load in the case of asymmetrical mass abrasion.With considering the axis drag force that can reflect the continuous varying of projectile nose shape，a method is proposed to analyze the yielding of a normal penetrating projectile under the combination of compression and bending due to asymmetrical mass abrasion.It indicates that the critical yielding cross-section of a projectile is very much sensitive to the transverse load induced by asymmetrical mass abrasion when it suffers large axis drag force.

mechanics of explosion；bending；asymmetrical mass abrasion；normal penetration projectile；yielding；concrete target

30January 2010；Revised 18April 2010

CHEN Xiao-wei，chenxiaoweintu＠yahoo.com

（责任编辑 张凌云）

O385 国标学科代码：130·3530

A

1001-1455（2011）02-0119-08＊

2010-01-30；

2010-04-18

国家自然科学基金项目（51021001）；中国工程物理研究院学科发展基金重点项目（2009A0201009）；中国工程物理研究院“双百人才”基金项目（ZX04001）

赵 军（1981— ），男，博士，工程师。

Supported by the National Natural Science Foundation of China（51021001）