长杆和分段杆侵彻的数值模拟*
2011-01-22陈小伟雷劲松
郎 林,陈小伟,2,雷劲松
(1.西南科技大学土木工程与建筑学院,四川 绵阳 621010;
2.中国工程物理研究院总体工程研究所,四川 绵阳 621900)
长杆和分段杆侵彻的数值模拟*
郎 林1,陈小伟1,2,雷劲松1
(1.西南科技大学土木工程与建筑学院,四川 绵阳 621010;
2.中国工程物理研究院总体工程研究所,四川 绵阳 621900)
利用ANSYS/LS-DYNA程序,采用Lagrange方法和Johnson-Cook本构模型,对长径比为5的平头钨合金长杆弹、分段体长径比为1的理想分段杆和带套筒的分段杆侵彻半无限厚钢靶进行了三维数值模拟。给出了侵彻过程中典型时刻的物理图像,并对3种杆的侵彻性能进行了比较。结果表明:分段杆侵彻深度的主要贡献在相Ⅲ惯性扩孔阶段而非连续长杆的相Ⅱ准定常侵彻阶段;分段间隔对侵彻深度的增加有显著影响;套筒的贡献主要在于弹坑直径的增加而对侵深影响微小。
固体力学;侵彻深度;Johnson-Cook本构模型;分段杆;半无限靶
近几十年来,长杆弹侵彻理论得到了较快发展,如被公认的描述长杆侵彻机理最成功的一维理论模型Alekseevskii-Tate模型[1-2]。侵彻机理的研究表明,在长杆弹质量一定的条件下,杆弹的侵彻深度随着撞击速度和长径比的增大而增大。因此,增大穿甲弹长径比是提高穿甲弹威力的主要途径,但是长径比过大会造成着靶攻角、弹道偏移、不易发射等问题。
20世纪80年代发现由若干分段体组成的分段体链(即分段杆)的侵彻效率得到提高,于是人们开始关注分段杆的研究[3]。对分段杆的侵彻机理已进行了一些的实验研究和数值模拟,如B.R.Sorensen等[4]和J.H.Cuadros[5]分别做了分段杆高速撞击钢靶板的实验,得出了在广泛速度范围内分段杆侵彻能力高于相应的连续长杆。X.M.Wang等[6]对较低速度(约2.0km/s)下分段杆打击钢靶进行了实验,结果表明在较低速度下分段杆的侵彻能力一样,比相应的连续长杆的侵彻能力有所提高。
本文中,针对较低速度(约2km/s)的分段杆侵彻问题,对长径比为5的平头钨合金长杆弹、分段体长径比为1的理想分段杆和带套筒的分段杆侵彻半无限钢靶分别进行三维数值模拟,给出侵彻过程中典型时刻的物理图像,将模拟的侵彻深度和实验数据进行比较,并分析连续长杆、理想分段短杆和带套筒的分段杆的侵彻性能。
1 有限元模型及验证
1.1 弹靶材料本构关系
采用Johnson-Cook强度模型和累积损伤失效模型描述弹靶材料的力学性能[7],具体形式为

式中:A、B、C、n、m 为材料常数;εp是累积塑性应变;=是量纲一应变率,其中为塑性应变率,为参考应变率;T*=(T-Tr)/(Tm-Tr)为量纲一温度,其中Tm和Tr分别为材料的熔化温度和室温。材料损伤因子D介于0和1之间,D=0,材料无损伤;D=1,则材料完全损伤,有

式中:Δεp为一个时间步的塑性应变增量,εf为当前时间步的破坏应变,表达式为

式中:σ*=p/σeq为静水压力与等效应力之比,D1~D5为材料常数。
状态方程采用Grüneisen方程
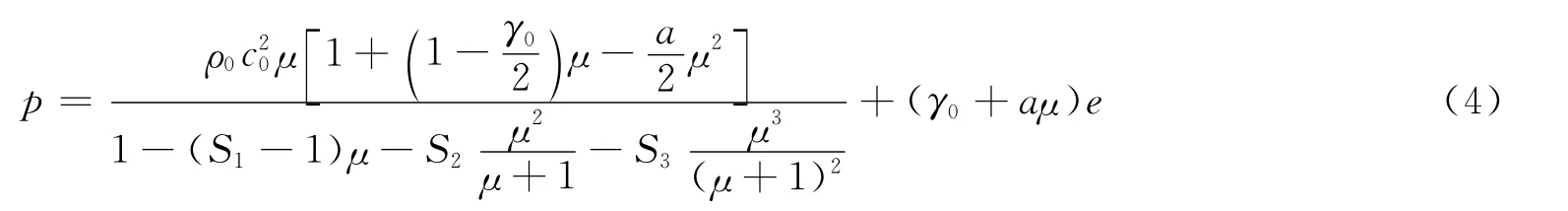
式中:e为材料的内能;c0为vs-vp曲线的截距;S1、S2和S3为vs-vp曲线斜率的系数;vs为击波速度;vp为质点速度;γ0为Grüneisen系数;a是对γ0的一阶体积修正;μ=ρ/ρ0-1,ρ为当前密度,ρ0为初始密度。
侵彻过程为绝热过程,温升按下式描述

式中:σeq和εeq分别为等效应力和等效应变;ρ为材料密度;cp为比定压热容;χ是Taylor-Quinney系数,取0.9。
套筒采用Plastic-Kinematic材料模型,本构方程为
(6)文稿中的量和单位应符合国家标准。外文字母的正斜体、大小写等须写清楚,上下角的字母、数据和符号的位置皆应明显区别。

式中:σ0为静屈服应力为应变率;C、P为应变率效应参数为等效塑性应变;Ep=EtanE/(EEtan)为塑性硬化模量;β为硬化模式参数。
表1给出了钨合金、钢靶和铝套筒3种材料的相关物性参量,主要参考文献[8]。

表1 3种材料的模型参数Table 1 Model parameters for three materials
1.2 弹靶有限元模型
采用ANSYS/LS-DYNA对连续长杆和分段杆侵彻半无限钢靶进行数值分析,取1/4结构进行三维模拟计算,设定靶板外表面为应力无反射界面,以模拟无限域。
弹体为3种类型的钨合金弹,直径均为7mm。弹靶建模如图1所示,第1种弹为连续长杆,长径比L/D=5,弹长35mm;第2种弹为理想分段杆,由5个长径比为1的分段体组成,间隔14mm,间隔与弹径比S/D=2,弹体总长度为91mm,质量与连续长杆相同;第3种弹为带套筒的分段杆,直径、分段体间隔和弹体总长度与理想分段杆的相同,但在分段体外固接一厚2.2mm的铝套筒。靶板为RHA钢板,尺寸为Ø70mm×100mm。
网格均用Lagrange映射网格划分方法,网格单元形状为八节点六面体,弹、靶单元类型均采用SOLID164。弹体单元尺寸均为0.3mm×0.3mm×0.3mm,靶心单元尺寸为0.3mm×0.3mm×0.3 mm,离靶心较远部分网格比例加大,以减少计算机时。弹靶之间采用三维面对面侵蚀接触算法。

图1 在数值模拟中3种弹体的剖面图及靶板网格Fig.1Schematics of the three types of rods and the target used in numerical simulation
1.3 模型验证
利用连续长杆及分段杆的实际弹道实验[5]作为数值计算的模型验证。如表2所示,计算值与实验结果之间的最大误差不超过10%,表中v0为初始撞击速度,h为侵彻深度。

表2 实验数据与计算结果Table 2 Experimental data and numerical results
2 数值模拟结果与分析
2.1 长杆弹侵彻
D.L.Orphal[9]建议长杆侵彻金属靶可分为4相。相I是初始撞击瞬时相,作为开坑阶段,侵彻深度相当于数倍杆径。在相Ⅱ准定常阶段,弹、靶以半流体方式变形,需同时考虑弹、靶材的强度效应,采用Alekseevskii-Tate模型描述。杆体完全侵蚀后,相Ⅲ侵彻开始,包括2次侵彻和后流体侵彻;其中,2次侵彻指弹体侵蚀后的残余物造成的剩余侵彻,要求弹体密度大于靶体密度且侵彻速度较高;后流体侵彻是指弹坑附近区域因尚有动能而进一步变形导致侵彻深度增加。后流体侵彻较2次侵彻更易发生,两者也可同时发生。最后是相Ⅳ,即靶体的弹性恢复,变形较小,常被忽略。
长杆弹的侵彻过程及von Mises应力分布如图2所示。图3(a)给出了弹靶接触面压力时间历程,而图3(b)则给出了长杆弹头侵彻速度和弹尾速度时间历程。由图2~3可知,数值结果与D.L.Orphal[9]所建议的侵彻4相非常吻合;长杆侵彻的弹坑深度主要由相Ⅱ阶段准定常过程完成。另外,相关计算也表明Lagrange方法和Johnson-Cook本构模型适合于较低速度长杆弹侵彻的数值模拟。
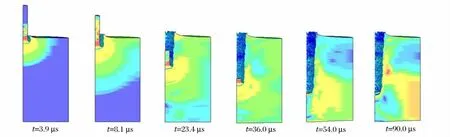
图2 初始撞击速度为2.0km/s时,侵彻过程中长杆弹和半无限钢靶的von Mises应力分布Fig.2 Von Mises stress contours of the long rod and semi-infinite steel target during penetration at the initial impact velocity of 2.0km/s
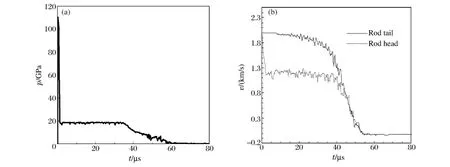
图3 初始撞击速度为2.0km/s时,长杆弹侵彻半无限钢靶的弹靶接触面压力、侵彻速度和弹尾速度时间历程Fig.3 Projectile-target interface pressure and velocity histories for a long rod penetrating into a semi-infinite steel target at the initial impact velocity of 2.0km/s
2.2 理想分段杆侵彻
理想分段杆的侵彻过程及von Mises应力分布如图4所示,而图5给出了理想分段杆侵彻钢靶的弹靶接触面压力和各分段杆头尾速度时间历程。由于理想分段杆对半无限钢靶的侵彻相当于5个长径比为1的短杆对靶体的先后连续侵彻,因此可分析单个分段体的侵彻过程。

图4 初始撞击速度为2.0km/s时,侵彻过程中理想分段杆和半无限钢靶的von Mises应力分布Fig.4 Von Mises stress contours of the ideal segmented rod and semi-infinite steel target during penetration at the initial impact velocity of 2.0km/s
短杆与长杆侵彻有着本质上的不同。由图4~5可知,短杆侵彻无法形成准定常阶段,其主要侵彻阶段仅与相Ⅲ相似。根据计算结果,还可进一步分析其侵彻特点。如图4所示,在0~1.5μs时间段应力波还未传到分段体尾部,分段体尾部速度仍为初始速度2.0km/s;然而应力波很快就传到分段体尾部,所以各个分段体的头、尾速度几乎相等(见图5(b))。在t=6.6μs时分段体几乎侵蚀殆尽,仅余侵蚀后的残余物侵彻靶体,靶体侵深继续缓慢增加,分段体直至近16.5μs最终被完全侵蚀。
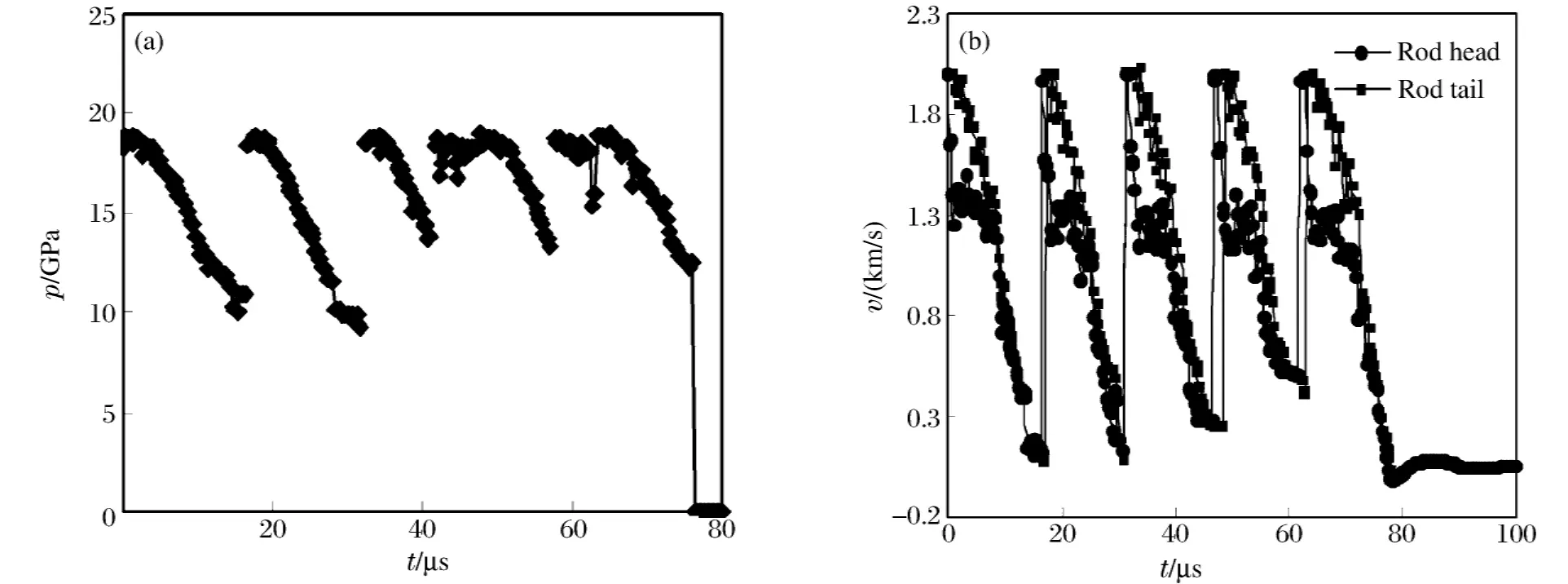
图5 初始撞击速度为2.0km/s时,理想分段杆侵彻半无限钢靶的弹靶接触面压力、侵彻速度和弹尾速度时间历程Fig.5 Projectile-target interface pressure and velocity histories for an ideal segmented rod penetrating into a semi-infinite steel target at the initial impact velocity of 2.0km/s
从图5(a)中可以看出各分段体侵彻时其弹靶接触面压力都在10~18GPa范围内单调下降,相当于相Ⅲ阶段的压力时间历程。这也说明分段短杆侵彻钢靶主要贡献在相Ⅲ惯性扩孔阶段而非长杆侵彻中占主要贡献作用的准定常阶段。图5(b)给出的整个分段杆侵彻靶板的速度时间历程,表明每个分段体在与靶体侵彻时速度下降很快(各曲线间几乎平行),各分段体初始撞击速度恒为2.0km/s。
2.3 带套筒的分段杆侵彻
图6给出了带套筒分段杆的侵彻过程及相应弹靶von Mises应力分布图。各分段体的侵彻和理想分段体侵彻类似,仍类似于相Ⅲ阶段。附着的套筒在钨合金分段体的挤压作用下向外扩张且发生质量侵蚀,对侵彻深度贡献甚小。t=0~8.7μs时间段为首个分段体侵彻阶段,相应的套筒向外扩张且发生质量侵蚀和破碎,同时破碎套筒的飞溅物向外流动,套筒的向外扩张导致弹坑扩大。但在2个分段体侵彻之间,套筒则不再向外扩张,转而变化为向内收缩;尽管其质量不断侵蚀,但侵深并未增加,原因在于套筒为铝材(弱于钢)。甚至在后续的分段体撞击时,还需先与向内收缩的套筒作用后再侵彻靶体,这将消耗部分能量。因此在实际的分段杆设计时,需对套筒进行材料和几何优化。

图6 初始撞击速度为2.0km/s时,侵彻过程中带套筒分段杆和半无限钢靶的von Mises应力分布Fig.6 Von Mises stress contours of the segmented rod with a carrier tube and semi-infinite steel target during penetration at the initial impact velocity of 2.0km/s
图7给出了带套筒分段杆侵彻的弹靶接触面的压力和各分段体速度的时间历程。区别于理想分段杆侵彻,弹靶接触面压力维持在15~18GPa,且各分段杆撞击初速依次减小;各分段体侵彻过程中,弹头和弹尾的速度也有差异。其原因在于套筒与各分段体的相互作用,套筒在侵彻过程中一直保持受阻减速,该阻力势必通过套筒与分段体的连接作用而传递至后续的分段体,对全杆的侵彻起负作用。因此,实际分段杆设计中,应减弱套筒与分段体的作用,可通过削弱连接(胶联)、设计大于分段体直径的套筒内经(间隙用软物填塞)等方法实现。

图7 初始撞击速度为2.0km/s时,带套筒分段杆侵彻半无限钢靶的弹靶接触面压力、侵彻速度和弹尾速度时间历程Fig.7 Projectile-target interface pressure and velocity histories for a segmented rod with a carrier tube penetrating into a semi-infinite steel target at the initial impact velocity of 2.0km/s
3 3种弹型的侵彻过程比较
图8给出了3种杆体侵彻后的弹坑剖面图,连续长杆侵彻的弹坑直径与杆弹接近,类似直通,坑底呈尖锥形;理想分段杆的弹坑为糖葫芦形,沿着侵彻深度方向弹坑直径逐渐减小;带套筒分段杆的弹坑坑壁和理想分段杆的相似,但弧的曲率更小,并且随着侵彻深度的增加弧线逐渐变小,2种分段杆的弹坑直径都比连续长杆的大。
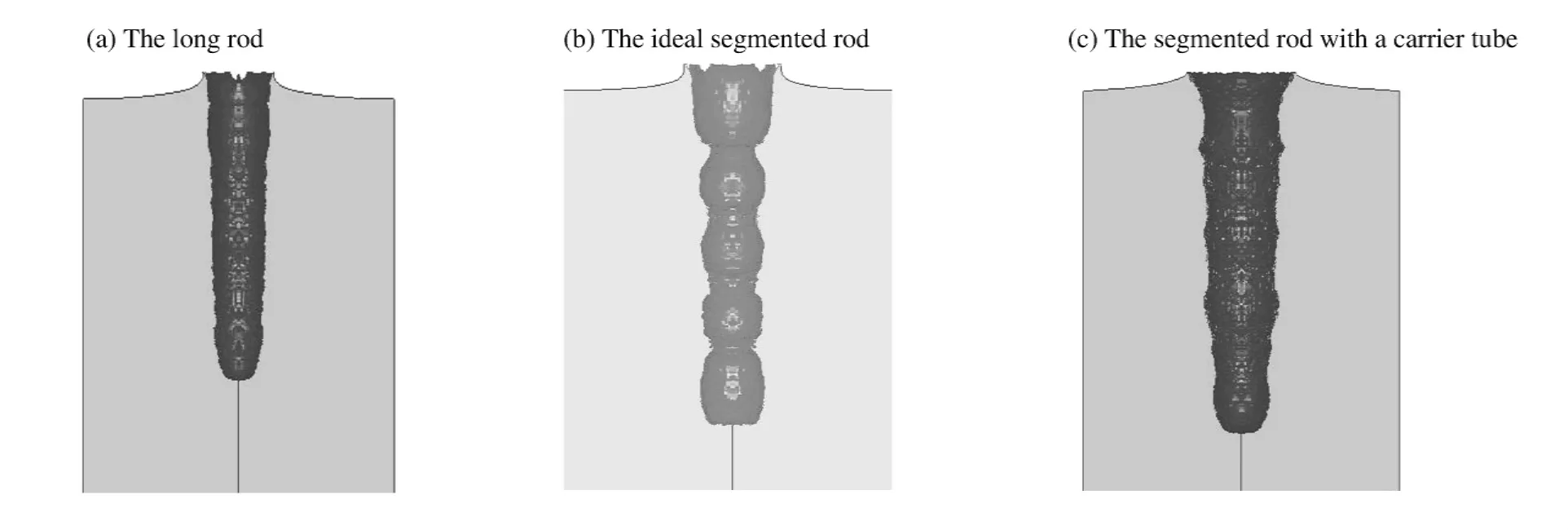
图8 3种弹体侵彻靶体后的弹坑剖面图Fig.8 Crater profiles after the three types of rods penetrating into steel targets
图9给出了3种弹型分别侵彻靶体的侵彻深度随时间的变化。显然,连续长杆侵彻深度呈线性增加,而理想分段杆和带套筒分段杆的侵彻深度由5个弧段组成,表明分段体间隔的存在,在间隔时间段内侵彻深度仍缓慢增加。理想分段杆和带套筒的分段杆在前2个弧段侵彻深度几乎重合,但从第3个弧段开始带套筒分段杆的弧段比理想分段杆的弧段长。这是由于套筒也参加了对靶体的侵彻,从而导致最终的侵彻深度比理想分段杆的侵彻深度稍大,但显然套筒对侵彻深度的贡献很小。
图10描绘了靶板和长杆/分段杆的动能时间历程的数值预期。钨合金杆的初始动能在3种弹型中是相同的,靶体获得的动能很少,然而这些能量消耗殆尽的时间是不同的。理想分段杆消耗时间明显比连续长杆要长,这是由于分段体间隔导致弹体总长增加,在分段体间隔时间内发生了2次侵彻和后流体侵彻;而带套筒的分段杆比理想分段杆略有增加。由于套筒导致分段杆整体性得到提高,带套筒分段杆的动能变化曲线比理想分段杆的动能变化曲线更光滑,弹坑剖面变得平滑,如图8(c)所示。随着各分段体的冲击速度减小,沿侵深方向对应于每个分段体的圆齿形截面直径也在减小。
需指出的是,图10(c)中的套筒初始动能几乎是钨合金杆的2/3,也即带套筒分段杆的初始能量比理想分段杆多60%,然而其侵深却仅增加约4%,缘于套筒大部分动能贡献于弹坑直径扩张。

图9 初始撞击速度为2.0km/s时,3种弹体侵彻深度时间历程Fig.9 The depth of penetration as a function of time for the three types of rods penetrating into steel targets at the initial impact velocity of 2.0km/s

图10 初始撞击速度为2.0km/s时,3种弹体的各部分和靶板的动能时间历程Fig.10 Kinetic energy as a function of time for the different rods and targets at the initial impact velocity of 2.0km/s
4 结 语
通过对连续长杆、理想分段杆和带套筒的分段杆的侵彻性能的三维数值模拟,研究表明:分段杆侵彻深度的主要贡献在相Ⅲ惯性扩孔阶段而非连续长杆的相Ⅱ准定常侵彻阶段;分段间隔对侵彻深度的增加有显著的影响;套筒的贡献主要在于弹坑直径的增加而对侵彻深度的影响微小。研究结果对分段杆式穿甲弹的实用化研究具有参考价值。
[1]Alekseevskii V P.Penetration of a rod into target at high velocity[J].Combustion,Explosion,and Shock Waves,1966,2(2):63-66.
[2]Tate A.A theory of the deceleration of long rods after impact[J].Journal of the Mechanics and Physics of Solids,1967,15(6):387-399.
[3]Orphal D L,Miller C W.Penetration performance of non-ideal segmented rods[J].International Journal of Impact Engineering,1991,11(4):457-461.
[4]Sorensen B R,Kimsey K D,Silsby G F,et al.High velocity penetration of steel targets[J].International Journal of Impact Engineering,1991,11(1):107-109.
[5]Cuadros J H.Monolithic and segmented projectile penetration experiments in the 2to 4kilometers per second impact velocity regime[J].International Journal of Impact Engineering,1991,10(2):147-157.
[6]Wang X M,Zhao G Z,Shen P H.High velocity impact of segmented rods with an aluminum carrier tube[J].International Journal of Impact Engineering,1995,17(8):915-923.
[7]Johnson G R,Cook W H.A constitutive model and data for metals subjected to large strains,high strain rates and high temperature[C]∥Proceedings of the 7th International Symposium on Ballistics.Hague,Netherlands:International Ballistics Committee,1983:541-547.
[8]兰彬,文鹤鸣.钨合金长杆弹侵彻半无限钢靶的数值模拟及分析[J].高压物理学报,2008,22(3):245-252.
LAN Bin,WEN He-ming.Numerical simulation and analysis of the penetration of tungsten-alloy long rod into semi-infinite armor steel targets[J].Chinese Journal of High Pressure Physics,2008,22(3):245-252.
[9]Orphal D L.Phase three penetration[J].International Journal of Impact Engineering,1997,20(6/7/8/9/10):601-616.
Numerical simulations on long rod and segmented rods penetrating into steel targets*
LANG Lin1,CHEN Xiao-wei1,2,LEI Jing-song1
(1.School of Civil Engineering,Southwest University of Science & Technology,Mianyang 621010,Sichuan,China;
2.Institute of Structural Mechanics,China Academy of Engineering Physics,Mianyang 621900,Sichuan,China)
Numerical simulations were conducted on the penetration of the long rod with the length-radial ratio of 5,the ideal segmented rod and the segmented rod with a carrier tube into semi-infinite steel targets,respectively,by using the software ANSYS/LS-DYNA3D.The Lagrangian method and Johnson-Cook constitutive model were coupled in the numerical simulations.The von Misese stress contours were given at the typical times during the penetration and the penetration performances of these rods were compared.Comparison shows that the dominant contribution to the depth of penetration(DOP)of the segmented rod is due to the phaseⅢnon-steady stage rather than the phaseⅡquasi-steady penetration stage in the long-rod penetration.The interspacing of the segmented rods has a significant impact on the DOP,while the carrier tube only contributes to the increase of the crater diameter.
solid mechanics;depth of penetration;Johnson-Cook model;segmented rod;semi-infinite steel target
15October 2009;Revised 25February 2010
CHEN Xiao-wei,chenxiaoweintu@yahoo.com
(责任编辑 张凌云)
O347 国标学科代码:130·15
A
1001-1455(2011)02-0127-08*
2009-10-15;
2010-02-25
国家自然科学基金项目(10672152)
郎 林(1984— ),男,硕士,工程师。
Supported by the National Natural Science Foundation of China(10672152)
