抛物线双切三角形的性质初探

● (枣庄市第十八中学 山东枣庄 277200)

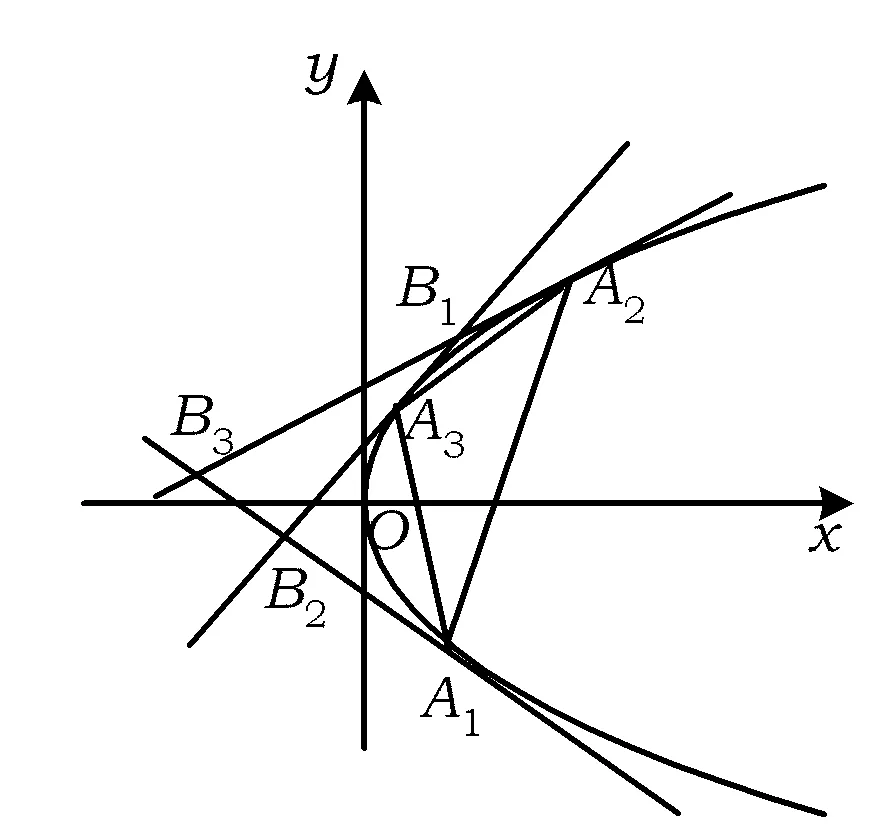
图1

我们知道，过抛物线y2=2px(p>0)上不同的3个点Ai(xi,yi)(i=1,2,3)作切线可围成△B1B2B3(如图1)，则△A1A2A3和△B1B2B3分别被称作抛物线的切点三角形和切线三角形(简称“抛物线双切三角形”).这样，以抛物线、切线、三角形等知识为线索，可构造出一类“抛物线双切三角形”的相关问题.本文拟对此类问题的性质作初步探讨，与大家共赏.

抛物线双切三角形具有一系列有趣的性质.为行文方便，设“双切三角形”所在的抛物线方程为：y2=4px(p>0).

首先给出有关的3条引理(证明略).

引理1过抛物线上不同的2个点切线交点的横坐标是2个切点横坐标的比例中项；纵坐标是2个切点纵坐标的平均数.

引理2抛物线焦点弦的2个端点的纵坐标之积为常数.

引理3抛物线的焦点在其切线上的射影的轨迹是这条抛物线顶点处的切线.

下面给出并证明“抛物线双切三角形”的若干性质：

性质1抛物线切点三角形面积是切线三角形面积的2倍.

证明如图1，设抛物线的切点△A1A2A3顶点Ai(i=1,2,3)的坐标分别为(pλ2,2pλ)，(pu2,2pu)，(pv2,2pv).由引理1知，抛物线的切线△B1B2B3顶点Bi(i=1,2,3)的坐标依次为(puv,p(u+v)),(pvλ,p(v+λ)),(pλu,p(λ+u)).根据三角形面积公式，可得

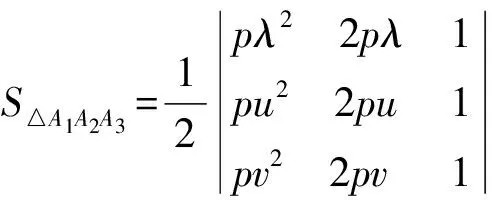
p2|(u-v)(v-λ)(λ-u)|，

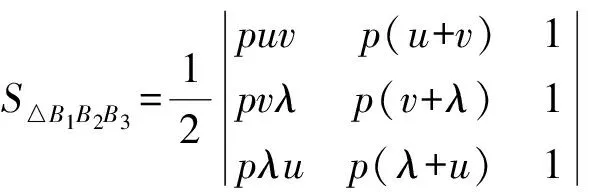
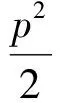
因此

S△A1A2A3=2S△B1B2B3.

由以上证明可知，性质1有如下推论：

推论1抛物线的切点△A1A2A3(亦称“抛物线的内接三角形”)的面积为

其中yi(i=1,2,3)是抛物线的切点△A1A2A3顶点Ai(xi,yi)的纵坐标.

性质2抛物线切点三角形各顶点到焦点的距离之积等于切线三角形各顶点到焦点的距离之积.

证明如图2，设“双切三角形”所在的抛物线方程为：y2=4px(p>0)，则焦点为F(p,0).再设抛物线的切点△A1A2A3顶点Ai(xi,yi)(i=1,2,3)的坐标分别为(pλ2,2pλ)，(pu2,2pu)，(pv2,2pv)，由引理1知，抛物线的切线△B1B2B2顶点Bi(xi′,yi′)(i=1,2,3)的坐标分别为(puv,p(u+v)),(pvλ,p(v+λ)),(pλu,p(λ+u)).由两点间的距离公式，得

AiF2=(xi-p)2+(yi-0)2(i=1,2,3).

于是

A1F2=p2(λ2+1)2,

A2F2=p2(u2+1)2,A3F2=p2(v2+1)2.

同理可得

BiF2=(xi′-p)2+(yi′-0)2(i=1,2,3),

即

B1F2=p2(u2+1)(v2+1),

B2F2=p2(v2+1)(λ2+1),

B3F2=p2(λ2+1)(u2+1).

由上述证明，不难证得性质2有如下推论：

图2

图3

推论2过抛物线上不同两点的切线的交点与其焦点的连线是过两切点的焦半径的比例中项.

推论3过抛物线上不同两点的切线的交点与其焦点的连线平分过两切点的焦半径的夹角.

性质3若抛物线切点三角形各顶点处的法线共点，则切点三角形各顶点到其焦点的距离之和为定值.

证明如图3，设抛物线的切点△A1A2A3的顶点Ai(xi,yi)(i=1,2,3)处的法线共点于M(α,β)，则可推知：yi(i=1,2,3)是方程y3+4p(2p-α)y-8p2β=0的3个根.由韦达定理得

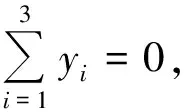
即

y1y2+y2y3+y3y1=4p(2p-α)，

又因为点Ai(xi,yi)(i=1,2,3)在抛物线y2=4px(p>0)上，所以

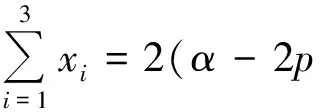
由抛物线的定义，得

FAi=|xi+p|(i=1,2,3)，

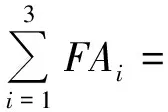
(因为点F，O，M均为定点).

性质4抛物线切线三角形的垂心必在抛物线的准线上.

证明如图4，设抛物线的切点△A1A2A3顶点Ai(i=1,2,3)的坐标分别为(pλ2,2pλ)，(pu2,2pu)，(pv2,2pv).由引理1知，抛物线的切线△B1B2B3顶点Bi(xi′,yi′)(i=1,2,3)的坐标依次为(puv,p(u+v)),(pvλ,p(v+λ)),(pλu,p(λ+u)).又过点B1向过点A1的切线λy=x+pλ2所作垂线的方程为

由此，垂线(1)与抛物线的准线l：x=-p的交点H的纵坐标为

由于式(2)是关于λ,u,v对称的，因此抛物线的切线△B1B2B3的垂心就是H.故抛物线的切线三角形的垂心必在抛物线的准线上.

图4

图5

性质5抛物线切点三角形与切线三角形重心的连线必平行于抛物线的(对称)轴.

证明如图5，设抛物线的切点△A1A2A3顶点Ai(i=1,2,3)的坐标分别为(pλ2,2pλ)，(pu2,2pu)，(pv2,2pv).由引理1知，抛物线的切线△B1B2B3顶点的坐标依次为(puv,p(u+v)),(pvλ,p(v+λ)),(pλu,p(λ+u)).依据三角形的重心坐标公式得

因此重心GA,GB连线的方程为

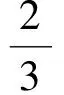
图6

故重心GA,GB的连线必与抛物线的对称轴平行.

性质6抛物线切点三角形的各边在准线上的射影之和是切线三角形各边在准线上射影之和的2倍.

证明如图6所示，设抛物线的切点△A1A2A3顶点Ai(i=1,2,3)的坐标分别为(pλ2,2pλ)，(pu2,2pu)，(pv2,2pv).由引理1知，抛物线的切线△B1B2B3顶点Bi的坐标依次为(puv,p(u+v)),(pvλ,p(v+λ)),(pλu,p(λ+u)).过顶点Ai,Bi作准线l的垂线，垂足分别为Q,R,K和M,N,S.又抛物线的准线l的方程为：x=-p，且l∥y轴.这里不妨把抛物线的切点△A1A2A3的3边A1A2,A2A3,A3A1在准线上的射影记作射影lAiAj，同理记射影lBiBj.于是

射影lAiAj=点Ai与点Aj的纵坐标差的绝对值，

射影lBiBj=点Bi与点Bj的纵坐标差的绝对值.

射影lA1A2+射影lA2A3+射影lA3A1=

2p(|λ-u|+|u-v|+|v-λ|);

射影lB1B2+射影lB2B3+射影lB3B1=

p(|λ-u|+|u-v|+|v-λ|)，

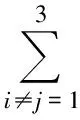
由此可知，性质6有以下推论：

推论4若自抛物线外一点引它的2条定切线，则夹在这2条定切线间的动切线，与其相交成的动线段在此准线上的射影为定长.

推论5若自抛物线外一点引它的2条切线，则2条切线长在其准线上的射影相等.

性质7若抛物线切点三角形的一条边过其焦点，则抛物线的切线三角形一定是直角三角形.

证明如图7，设过抛物线的焦点F的切点△A1A2A3的一边A1A2的2个端点坐标为Ai(xi,yi)(i=1,2)，则有切线A1B3，A2B3的方程为

yyi=2p(x+xi)(i=1,2),

因此切线A1B3，A2B3的斜率为

于是

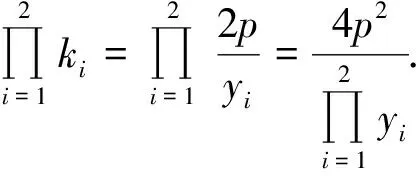
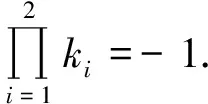
于是A1B3⊥A2B3，故切线△B1B2B3是直角三角形.

由上可知，性质7的逆命题亦是真命题.

性质7′ 若抛物线的切线三角形是直角三角形，则抛物线切点三角形必有一条边过其焦点.

除此，性质7′还有如下推论：

推论6过抛物线焦点弦的2个端点的切线互相垂直.

推论7抛物线的切线三角形是直角三角形的直角顶点的轨迹是其抛物线的准线.

上述性质7′及性质7′的推论请读者自行证明，本文从略.

图7

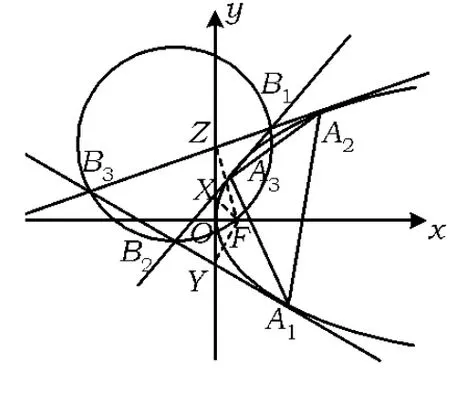
图8

性质8抛物线切线三角形的外接圆必过其抛物线的焦点.

证明如图8，过抛物线的焦点F作其切线B1B2,B2B3,B3B1的垂线，设垂足为x,y,z.由引理3知，垂足x,y,z三点共线.又由西摩松线的逆定理得知：抛物线的焦点F必在抛物线的切线△B1B2B3的外接圆⊙B1B2B3上.

由此，可得性质8的相关推论：

推论8抛物线的焦点在切线三角形3条边上的射影必共线于抛物线顶点处的切线.

推论9切于3条已知直线的抛物线焦点的轨迹，是这3条已知直线所围成的抛物线切线三角形的外接圆.

推论10抛物线的焦点关于抛物线切线三角形3条边的对称点共线于抛物线的准线.

关于抛物线双切三角形的性质，还可以继续深化，但限于篇幅，仅到此为止.

[1] 吴振奎.中学数学证明方法[M].沈阳：辽宁人民出版社，1985.

[2] 李耀文.抛物线双切三角形及其性质[J].中学数学杂志:高中版，1999(3)：10-11.

[3] 杨世明.中国初等数学研究文集[M].郑州：河南教育出版社，1992.