高中数学联赛中的向量赛题解读

● (《数学竞赛之窗》编辑部 江苏苏州 215011)

高中数学联赛中的向量赛题解读

●王卫华(《数学竞赛之窗》编辑部 江苏苏州 215011)

向量问题自进入高中数学以来，因其自身具有的代数性和几何性的双重特征，以及和三角函数、解析几何、立体几何等知识的高度综合性，受到各级、各类考试命题者的青睐，迅速成为高考的必考问题.在高中数学联赛中，向量问题也很快成为考查的一个重点.本文拟就两者的对比，对全国高中数学联赛中的向量问题作一些解读，以期能够对广大读者有所裨益.

1 高考与高中联赛向量考查的重点比较

在高考考查中，向量问题常和三角函数、解析几何相综合，着重考查向量的基本性质和基本运算，更多的是作为问题转化的一个部分，而不是问题解决的重点.

在高中联赛中，向量问题往往具有纯粹性，着重考查选手对向量的本质特征——“数形二重性”的理解掌握，需要选手对题目中蕴含的几何本质有深入的了解，有很强的思维能力，以及敏锐的观察力.

2 高中联赛向量问题涉及的基本结论

在高中联赛的向量问题中，必须熟练掌握的基本结论有：

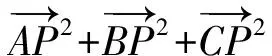
(4)若I为△ABC的内心，则

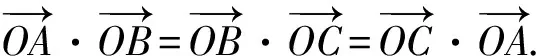
(6)设O为△ABC的外心，则

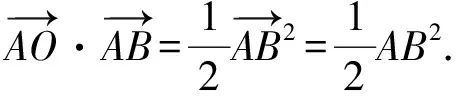
(7)设AB的中点为M，P为△ABC所在平面上一点，则

(8)设O，H分别为△ABC的外心和垂心，则

3 向量问题解题思路导析

高中联赛中的向量问题灵活多样，对选手的思维能力要求很高.以下通过对若干赛题的解题分析，给出思路探求的一些基本模式.

( )

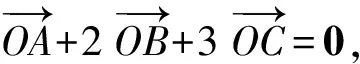
(2004年全国高中数学联赛试题)

则

从而点O为△AB1C1的重心，于是

故

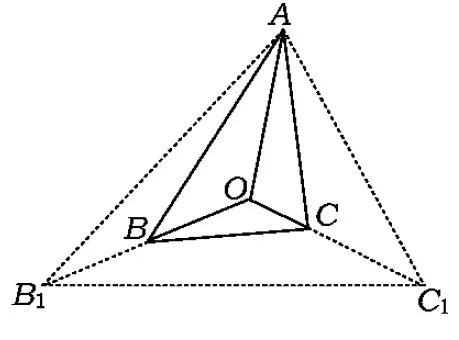
图1

图2

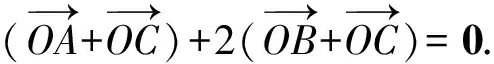
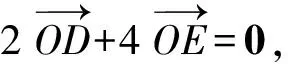
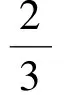
评析注意到:

S△BOC∶S△AOC∶S△AOB=1∶2∶3.

事实上，有一般的结论：

设O为△ABC内一点，记△BOC,△AOC和△AOB的面积分别为SA，SB，SC，则

易知，上述基本性质(1)和(4)均为本结论的特殊情形.

( )

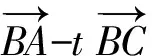
A．锐角三角形 B．钝角三角形

C．直角三角形 D．答案不确定

(2006年全国高中数学联赛试题)

分析本题有2种不同的思路:一种是考虑向量的几何意义，利用数形结合解题；另一种是通过平方将关于向量长度的不等式转化为关于向量的不等式解题.

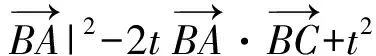
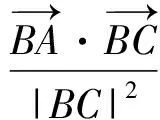
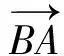
即

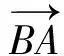
因此

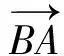
从而

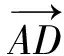
由此可得

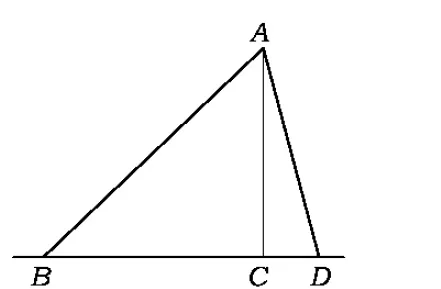
图3

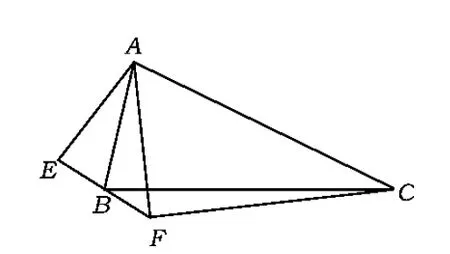
图4

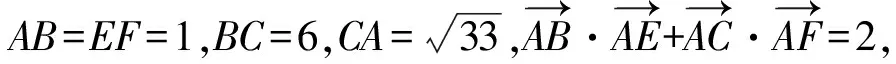
(2007年全国高中数学联赛试题)

分析本题的焦点在于如何处理2个关联的三角形.首先根据题设画一幅草图，由图4易知，可通过在三角形中应用余弦定理来求三角形对应边的数量积.

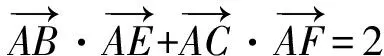
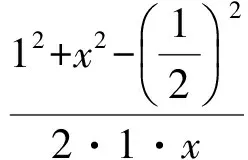
从而

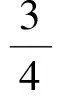
又在△AEF中，由中线长公式知

4AB2+EF2=2(AE2+AF2)，

从而

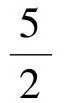
于是

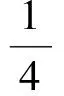
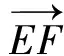
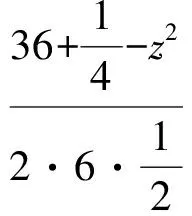
(2009年全国高中数学联赛湖北赛区预赛试题)

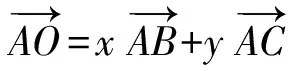
解因为O是△ABC的外心，所以

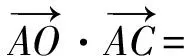
又

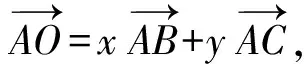
所以

即

于是

60x·cos∠BAC+100y=50.

由△ABC是锐角三角形，易知x≠0，因此

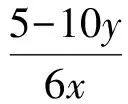
联赛中的向量问题除了直接考查以外，不可忽视向量作为一个工具的功能.这里不再举例说明.