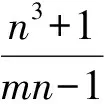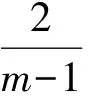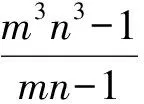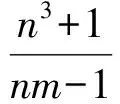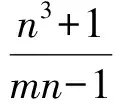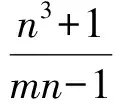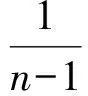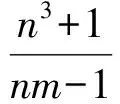简议整数问题中的常用方法
2010-11-23嵊州市第二中学浙江嵊州312400
● (嵊州市第二中学 浙江嵊州 312400)
简议整数问题中的常用方法
●张秋君(嵊州市第二中学 浙江嵊州 312400)
数论是专门研究整数问题的.由于整数具有离散性、有序性、无穷性等特点,因此以下方法就特别适合于解决数论问题.
1 不等式分析法
例1求方程x+y=x2-xy+y2的整数解.
解由方程有整数解,得
Δ=(y+1)2-4(y2-y)≥0,
解得

满足这个不等式的y值只有0,1,2.
当y=0时,由原方程可得
x=0或x=1;
当y=1时,由原方程可得
x=2或x=0;
当y=2时,由原方程可得
x=1或x=2.
故原方程有整数解
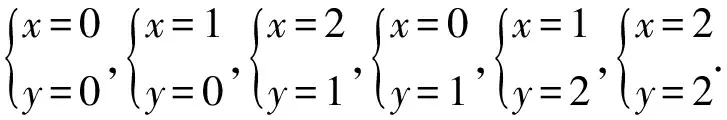
2 无穷递降法
例2确定并证明方程a2+b2+c2=a2b2的所有整数解.

2k>a1,2k>b1,2k>c1,

3 反证法
例3证明:方程x4+y4=z2没有正整数解.
证明假设原方程有一组正整数解(x0,y0,z0),并且z0是所有正整数解z中最小的.因此

其中(a,b)=1,a,b为一奇一偶.假设a为偶数,b为奇数,那么
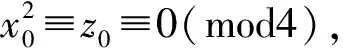
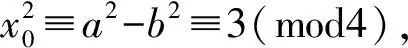

x0=p2-q2,b=2pq,a=p2+q2,
这里(p,q)=1,p>q>0,p,q为一奇一偶.从而
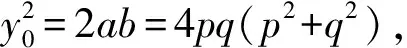
因为p,q,p2+q2两两互质,所以它们必须都是某整数的平方,即
p=r2,q=s2,p2+q2=t2,
从而
r4+s4=t2,
即(r,s,t)也是原方程的解,且有
t 这与z的最小性矛盾,故原方程无正整数解. 例4我们知道23+1=9有1个质因子,且32|23+1;232+1=513=33×19有2个质因子,且33|232+1,…,如此下去,可以猜想:k∈N*,23k+1至少有k个质因子,且3k+1|23k+1.试证明之. (2006年山东省第2届夏令营试题) 证明令ak=23k+1,则ak=3k+1bk,即要证bk是整数且有k-1个质因子.下用数学归纳法证明bk是整数. (1)当k=1时,结论显然成立. (2)假设当n=k时,结论成立.则当n=k+1时,因为 且 3k+1|ak, 所以 3k+2|ak+1, 由(1),(2)可知,bk+1是整数. 下证bk+1至少有k个质因子. bk+1=bkck. 由于(ck,3)=1,因此 (ck,bk)=1, 从而ck必有异于bk质因子的质因子,所以bk+1至少有k个质因子. 例5证明:存在无穷多个正整数,它们不能表示成少于10个奇数的平方和. 所以只有s=2,于是 又因为 所以 3|x1且3|x2, 因而9|n.但n=72k+66≡3(mod9),产生矛盾.从而n不能表示成少于10个奇数的平方和,且这样的n有无穷多个. 例6证明:方程2x2-5y2=7无整数解. 证明由2x2=5y2+7,可得y为奇数. (1)若x为偶数,则 2x2≡0(mod8), 因此 y2=(2n+1)2=4n(n+1)+1, 得 y2≡1(mod8),5y2+7≡4(mod8). 因为方程两边对同一整数8的余数不等,所以x不能为偶数. (2)若x为奇数,则 2x2≡2(mod4), 但 5y2+7≡0(mod4), 因此x不能为奇数. 综上所述,原方程无整数解. m-1=1或m-1=2, 故 (m,n)=(2,1)或(m,n)=(3,1). (2)若m=1,则 因此 n-1=1或n-1=2, 故 (m,n)=(1,2)或(m,n)=(1,3). 也是整数,于是m,n是对称的.不妨设m≥n. ①若m=n,则 为整数,于是n=2,m=2. ②若m>n,因为 n3+1≡1(modn),mn-1≡-1(modn), 所以 因此存在k∈N,使得 又 即 得k=1,于是 从而 解得 n-1=1或n-1=2, 因而 (m,n)=(5,3)或(m,n)=(5,2). 同理可得,当m (m,n)=(2,5)或(m,n)=(3,5). 综上所述,(m,n)可取(1,2),(2,1),(1,3),(3,1),(2,2),(2,5),(5,2),(3,5),(5,3).4 数学归纳法
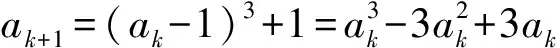
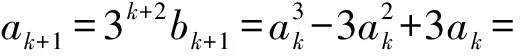
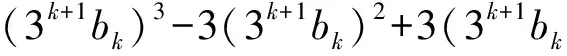
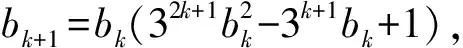
5 剩余类法(或称特殊模法)
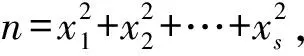

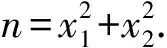

6 分类讨论法与奇偶分析法