从价值取向看高校自主招生数学笔试试题

● (舟山中学 浙江舟山 316000)

从价值取向看高校自主招生数学笔试试题

●谢建伟(舟山中学 浙江舟山 316000)

大学自主入学考试是对选拔优秀创新人才的一种新探索.自主招生是扩大了高校招生自主权、是深化高校招生录取制度改革的重要举措.由于其实施主体是大学，教育理念必然有了微妙的不同，考试性质又有某种特殊性，考试环境也更为宽松，其命题自然就有了值得玩味的一些新变化.

近几年来,高校自主招生表现出4大特点：

(1)招生比例不再受限.

“高校自主招生比例不得超过5%”的规定将被打破．这让不少高校能放心地增加招生计划，同时对优秀考生给予了更多的政策优惠．

(2)自主招生门槛降低.

高校自主招生权在增强，各高校自主招生的“门槛”却在走低，报名要求呈现降低的趋势．

(3)纷纷增加笔试环节.

相对于2009年，高校自主招生更加重视笔试这一环节．面试容易掺杂更多的主观成分，弹性空间太大；用笔试加面试的方式，可以更全面地衡量学生的素质．

(4)更加偏爱特殊才能.

高校的人才培养目标不同，所需要的学生特点也不同，这也就决定了各大高校越来越青睐有特殊才能的学生．

从上可见，自主招生的地位及权重已逐渐提升，甚至堪与普通高考相提并论，因此也越来越受到大家的关注．

本文以“价值取向”为视角，对自主招生笔试数学试题作一些剖析，旨在抛砖引玉．

1 基础性价值取向

数学知识和思维方法是数学解题的基础，基础又是走向未来的桥梁，自主招生对基础性层面的要求高于、广于普通课程意义上的高考．

1.1 知识性

对三基知识的了解与理解，高校教师自有其独特的视野.

例1设平面上有3个点，任意2个点之间的距离不超过1．问：半径至少为多大的圆盘才能盖住这3个点．请证明你的结论．

(2004年复旦大学自主招生数学笔试试题)

解设3个点为A，B，C,分情形讨论如下：

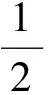
图1

图2

(2)若点A,B,C不共线，则构成△ABC,不防设A≤B≤C.

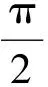
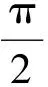
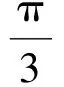
于是

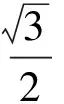
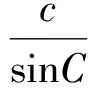
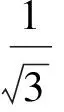
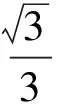
(2)自主招生笔试试题与高考试题相比，更注重知识变通性的考查.譬如,2006年复旦大学自主招生笔试试题中有一个求解三次方程的问题：

设k≥9，解方程:x3+2kx2+k2x+9k+27=0．

这道题目让那些只知道求根公式的高中学生望而怯步.表面上试题已超越中学生的知识范畴,实际上，只要将字母x与k的主客位置对换,化归为关于k的二次方程(视x为字母系数)，就不难得到方程有3个实根：

这种主客对换类题型在奥数中屡见不鲜.

1.2 方法性

代数方法、算术方法、几何方法是中学数学中的基本方法，使用时要领悟其精髓.譬如代数中的列方程解应用题，不仅是列方程，设未知数有时也是很关键的.

例2有一个整数的首位是7，当7换至末位时，得到的数是原数的三分之一，则原数的最小值是________．

(2003年上海交通大学自主招生数学笔试试题)

解法1(代数法):暂时弃去7，得其余部分数值为A，共有k位，则有方程

7×10k+A=(10A+7)×3,

即

29A=7×(10k-3).

以下就是做若干个9最后一个7，使其能被29整除的除法.当k=28时，

(10k-3)÷29=999…997÷29=

34 482 758 620 689 655 172 413 793，

乘以7即得

A=241 379 310 344 827 586 206 896 551.

故原数的最小值为

7241 379 310 344 827 586 206 896 551.

解法2(算术法)记原数为A，将7换至末位时，所得的数记为B，则A=3B.利用小学里的竖式乘法，可从个位开始，依次一位一位倒序求：乘积求得个位后，即在十位写上这一个数字；……，即把得来的积中的数字，错一位地复制到被乘数上，直至首次出现单个数字7为止.算法如下所示：

2 413 793 103 448 275 862 068 965 517

× 3

7 241 379 310 344 827 586 206 896 551

因此原数的最小值是

7 241 379 310 344 827 586 206 896 551.

评注(1)本例如像下面那样做：

5 862 068 965 517

× 3

7 586 206 896 551

那么得出最小值是7 586 206 896 551，

只要一检查，明显就知道是错的.因为最后一步得到的是15，加2得17，而不是单个7.

(2)该试题列方程求解，不容易想到要这样去设未知数列方程，然后还要做若干个9最后一个7除以29的试除法；用算术的一步步做倒序乘法，又有如上所述的陷阱；即使是在奥数中训练过同类的题目的学生，但数位之长，计算量之大，又大大地超越绝大多数师生之预想，有几人能坚持到28位，也实在是不敢奢望的.

2 应用性价值取向

加强应用意识,是新课程的一个重要导向.应用性也体现了数学学习的本意,其中包含有课程性和实践性这2个层面．

2.1 课程性

指课程上的基础知识的应用.

图3

(2010年清华大学等五校自主招生数学笔试试题)

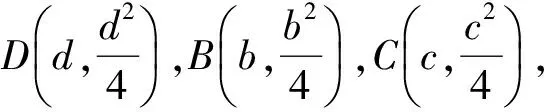
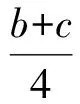
即

b+c=2d.

于是

即△ABC为直角三角形.

评注(1)看解答，似乎简单明了：先证得kAB+kAC=0,立即可知AD平分∠CAB.但是，“为什么能想到先去试证kAB+kAC=0”恰恰是解题关键之所在．

(2)圆锥曲线是中学课程的内容.本题是以圆锥曲线的一个几何性质：“过圆锥曲线C上一个定点M，作2条倾斜角互补的直线，交C于点A,B,则直线AB有定向”为几何背景.这里,直线AB总与曲线上点M′处的切线平行(M′与M关于对称轴对称,M′位于直线MA与MB之间)．

2.2 实践性

指知识应用到实际中.

例4为测量一工件内圆弧半径R，工人用3个半径均为r的圆柱形量棒O1,O2,O3放在如图4所示的与工件圆弧相切的位置上，通过深度卡尺测出卡尺水平面到中间量棒O2顶侧面的垂直深度(如图4).试写出R用h表示的函数关系式，并计算当r=10 mm,h=4 mm时，R的值．

(2007年上海交通大学自主招生数学笔试试题)

图4

图5

解取平面图思考，设AB为卡尺水平面位置，过点O1作O1H⊥OO2于点H，如图5.由条件知OO1=R-r=OO2，O1O2=2r，O1A=r，O2B=r+h,又ABHO1为矩形，得

BH=r,O2H=h，OH=R-r-h.

由勾股定理知

代入得

(R-r)2-(R-r-h)2=(2r)2-h2，

即

当r=10 mm,h=4 mm时，R=60 mm．

评注(1)早在上世纪30年代美国数学家克莱因就指出“数学为大家”.学习数学之根本目的在于研究并征服自然,笔试中不乏体现实用性价值的试题．

(2)本例要求学生能够实现从具体的感性事物到数学语言的抽象，从物体之间存在的位置关系到数量关系的转化.同时,这些事情本身又恰恰是建立于生活元素的观察、思考之上的(本例还可通过△OO1O2面积的2种求法求解).

3 发展性价值取向

高校自主招生对发展性的要求较高.主要表现在知识的前瞻性和解题的创造性层面上.求解这一类试题会让中学生感到相当棘手.

3.1 前瞻性

例5试构造函数f(x)，其定义域为(0,1)，值域为[0,1]，且对于任意a∈[0,1]，f(x)=a只有1个解.

(2006年复旦大学自主招生数学笔试试题)

解可以构造函数

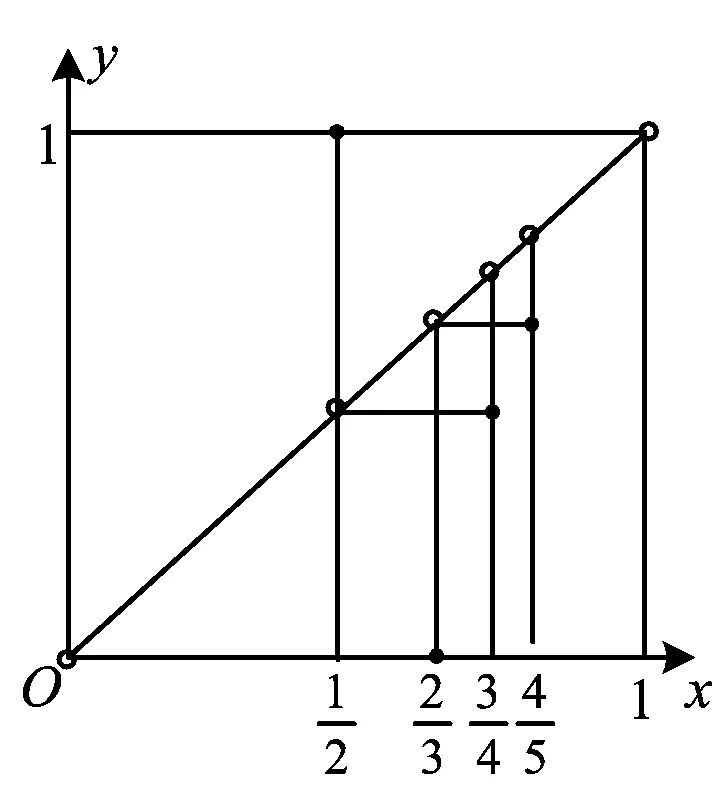
图6

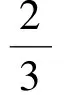
3.2 创造性

例6已知：

a1+a2+a3=b1+b2+b3;

(1)

a1a2+a2a3+a3a1=b1b2+b2b3+b3b1;

(2)

min{a1,a2,a3}≤min{b1,b2,b3},

(3)

求证：max{a1,a2,a3}≤max{b1,b2,b3}.

(2008年北京大学自主招生数学笔试试题)

证明不妨设a1≤a2≤a3，b1≤b2≤b3，则a1≤b1，下证a3≤b3即可．令

a1+a2+a3=b1+b2+b3=k，

利用均值代换，可设

其中p,q,r,s≥0，于是

代入式(2),得

由a1≤b1,得

由a1≤a2,得

由b1≤b2,得

式(6)+式(7),得

由式(4)，式(5)，式(8)得

因为

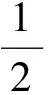
代入式(9),得

(1)若s+q=0,则

s=q=0,

代入式(4),得

r=p或3(r+p)-k=0.

由r=p，知a3=b3，即a3≤b3成立；由3(r+p)-k=0，知式(8)取到等号，因此

a1=a2=a3=b1=b2=b3，

即a3≤b3成立.

(2)若s+q>0，则由式(10)得

a3-b3≤0，

即a3≤b3也成立．

综上所述，命题得证．

评注(1)试题题干简约，题型或符号为中学生所熟悉，然而6个参量给出的条件之间的因果关系却一时难以看清，解答时又不知从何上手.需要学生具备良好的数学素养和创新能力．

(2)本例提供的解答过程构思巧妙，在发现对称性的基础上，对参量排序，再引入5个新参量k,p,q,r,s，借助均值代换，证明时多次实施逻辑推理、等价转换、分类讨论，可谓一环紧扣一环．

综上所述，自主招生笔试之价值取向，实际上要高于、深于、广于普通课程意义上的高考.但只要在日常教学过程中，对基础性、应用性、创造性给以足够的价值关注，付出更多的努力，就一定会收获更多的惊喜．

随着新课程的深化，许多自主招生类笔试试题与新课程理念相近，直接或稍加改编，便可引用为日常课堂教学的题例．

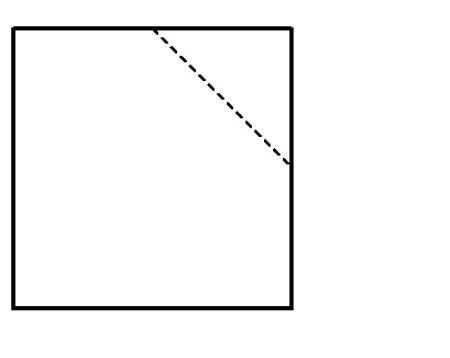
图7

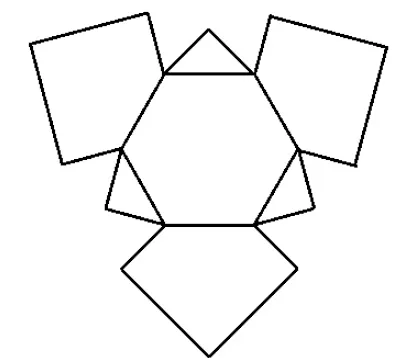
图8

例如,2005年上海交通大学保送生关于表面展开图的试题：

(答案：972)