议高中数学竞赛中的立体几何问题

● (绍兴市中等专业学校 浙江绍兴 312000)

议高中数学竞赛中的立体几何问题

●张佩丽(绍兴市中等专业学校 浙江绍兴 312000)

立体几何问题在高中数学竞赛中多以选择、填空题的形式出现.本文将立体几何在竞赛中出现的问题作一简单归纳，旨在抛砖引玉.

1 体积与体积比问题

例1如图1，在四面体ABCD中，P，Q分别为棱BC与CD上的点，且BP=2PC，CQ=2QD．R为棱AD的中点，则点A，B到平面PQR的距离的比值为________．

(2009年全国高中数学联赛江苏赛区初赛试题)

分析点A,B到平面PQR的距离分别为三棱锥APQR与BPQR的以三角形PQR为底的高,因此其比值等于这2个三棱锥的体积比．因为

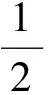
又

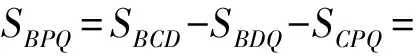
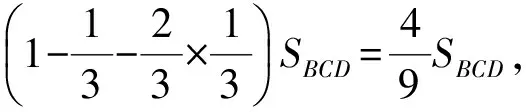
得

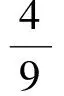
所以点A，B到平面PQR的距离的比为1∶4．

图1

图2

说明本题还可通过求出平面PQR与AB的交点来求此比值.如图2,在面BCD内，延长PQ，BD交于点M，则M为面PQR与棱BD的交点．由Menelaus定理，知

而

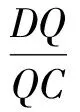
于是

在面ABD内，作射线MR交AB于点N，则N为面PQR与AB的交点．由Menelaus定理,知

而

于是

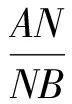
因此点A,B到平面PQR的距离的比为1∶4．

2 翻折问题

图3

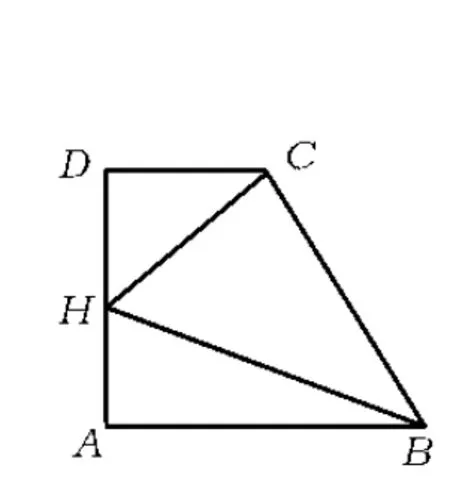
图4

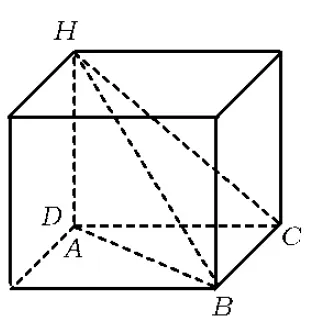
图5

(1)请在图中设计一种虚线，沿虚线翻折可成原来的三棱锥(指三棱锥的3个面);

(2)求这个三棱锥外接球的体积.

分析要解决此剪拼问题必须弄清4个面都直角三角形的三棱锥形状，仔细观察发现其中有3个直角三角形必须有1条直角边长相等.

(1)如图4,取AD的中点H，连结HC,HB，则HC,HB为设计的虚线.

(2)如图5,将三棱锥补成长方体.可视长方体的对角线为HB，其长就是外接球的直径

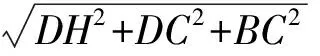
因此

说明第(2)小题还可利用取BH的中点O，证明OB=OH=OA=OC的方法求外接圆的体积.

3 最值问题

图6

分析分别沿BB1,A1C1和A1B1将E，F所在平面展开到同一平面内，分别计算得

或

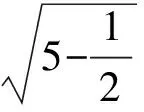
或

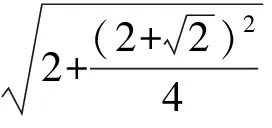
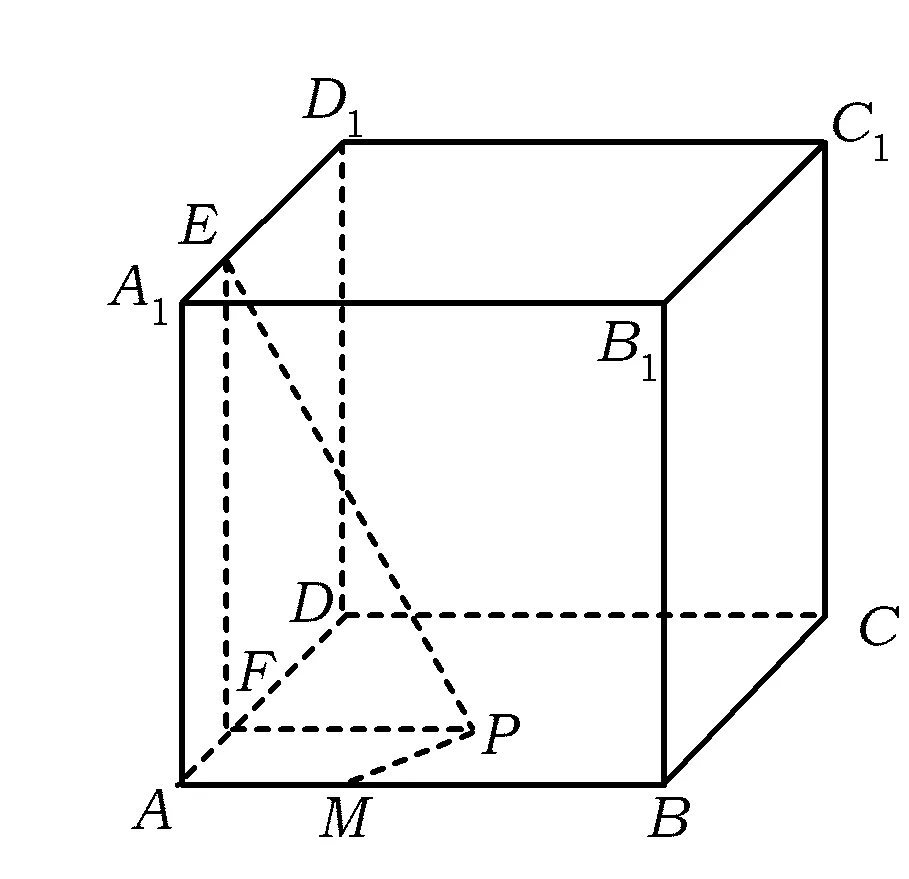
图7

4 轨迹问题

( )

A．抛物线 B．双曲线 C．直线 D．圆

分析作PF⊥AD于点F，作EF⊥AD于点E，连结EF，则PE是点P到直线A1D1的距离.由题意得，PE2-PM2=1.又PE2=PF2+1，从而PM=PF.在平面ABCD内，由抛物线定义知，所求点P的轨迹是抛物线.故选A.

说明本例用解析法求出点的轨迹方程，把立体几何中的轨迹问题转化成平面解析几何中的轨迹问题加以求解.

5 综合问题

例5正四棱锥P-ABC中相邻2个侧面所成二面角的大小为θ，则θ的取值范围是

( )

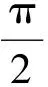
说明本题体现了有限与无限的转化.随着高中数学课程改革的逐步深入，对有限与无限思想的考查力度会不断加大.这是高考命题的一个新趋势.

例6已知正四面体ABCD的棱长为1cm,一只小虫从一个顶点沿棱爬到其余3个顶点是等可能的.

(1)这只小虫从点A出发，走了7cm，回到点A，中间经过点A一次，有多少种不同的路线？

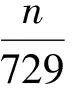
分析(1)这只虫子第2次回到点A，第1次回到点A可能是第2次，第3次，第4次，第5次,共4种情况.

(2)这只小虫爬行7cm有37种不同的爬法，其中回到点A的情况有以下几种：

①中间没回到点A；②中间回到点A一次；③中间回到点A两次.

解(1)这只虫子第2次回到点A，若第1次回到点A是第2次，则有32×23种.同理可得,第1次回到点A是第3次，第4次，第5次，均有32×23种，故共有32×23×4=288种不同的路线.

(2)这只小虫爬行7cm有37种不同的爬法，其中回到点A的情况有以下几种：

①中间没回到点A；②中间回到点A一次；③中间回到点A两次.

若中间没回到点A，有3×25种不同的爬法；若中间回到点A一次，有32×23×4种不同的爬法；若中间回到点A两次，只有第2次，第4次，或第2次，第5次，或第3次，第5次回到点A这3种可能，有33×2×3种.故回到点A的情况共有

3×25+32×23×4+33+2×3=546,

因此

得

n=182.

说明第(2)小题也可用递推思想，记Pn(n∈N*)为这只小虫从点A出发，走了ncm回到点A的概率,则

从而