简议分类讨论方法的应用

● (绍兴市高级中学 浙江绍兴 312000)

简议分类讨论方法的应用

●金定森(绍兴市高级中学 浙江绍兴 312000)

解题总是在一定范围(论域)内进行的.解题中有时要将题目条件包含的全体对象分成若干类,然后逐类讨论.因此,分类讨论是数学解题的一种重要策略.在分类时,首先要明确分类的对象和标准.有时还要对第一次分出的各类进行再分类,这就是第二级分类；类似地有第三级分类；……，这种进行多次分类的现象叫做连续分类.合理的分类不但是正确解题的出发点，而且是简捷解题的基础.

分类的原则是：不重不漏，即每一个题设包含的对象都必须在而且只在所分的一类中.为此，在分类时必须做到：(1)一次分类只按一个标准进行；(2)连续分类则按层次逐级进行.

1 由概念引起的分类

( )

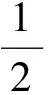
分析由题意得

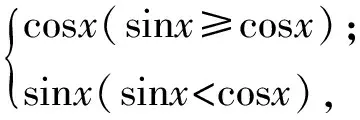
即f(x)等价于{sinx,cosx}min.故选C.

2 按图形位置分类

例2若四面体各棱的长是1或2，且该四面体不是正四面体，则其体积的值是________(写出所有可能的值).

分析要构造出满足条件的四面体，关键是根据三角形知识确定每个面上的3条棱，排除{1,1,2}，可得{1,1,1}；{1,2,2}；{2,2,2}，用这3类面(三角形)在空间中构造出满足条件的一个四面体.这就要进行分类讨论！

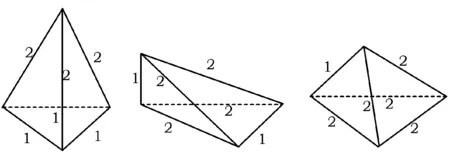
图1

3 按模的剩余类分类

例3求出所有的自然数n，使3个整数n，n+8，n+16都为质数.

分析现将所有自然数n按模为3的剩余类分成3类：n=3k，3k+1，3k+2.

当n=3k时，只有k=1时，3个整数3，11，19都是质数；

当n=3k+1时，

n+8=3k+1+8=3(k+3)

不是质数；

当n=3k+2时，

n+16=3k+2+16=3(k+6)

不是质数.

故满足题设的自然数只有一个3.

4 按数的大小分类

例4从写有数字111到999的3位数(其中的任一位数字不为0)卡片中任取1张，取得的3位数中任意2个数码之和能被第3个数码整除的3位数有________个.

分析设取得的符合要求的3位数的3个数码分别为a,b,c.

(1)若a

a+b<2c,

而a+b能被c整除，只有

a+b=c.

因为a+c能被b整除，b+c也能被a整除，所以这样的数组有1,2,3;2,4,6;3,6,9.组成的3位数共有18个.

(2)若a=b

c=2a.

这样的数组有1,1,2;2,2,4;3,3,6;4,4,8.组成的3位数有12个.

(3)若a=b=c,组成的3位数有9个.

综上所述,符合题意的3位数共有39个.

5 按相对位置分类

例5将7×7的棋盘中的2个方格染成黄色，其余的均染成绿色.若一种染色法可由另一种染色法经过将棋盘平面旋转后得到，则这样的2种染法应看作是同一种染色法，则有( )种不同的染色法.

A．298 B．300 C．306 D．309

分析将这个问题作如下分类讨论：

(1)当染成黄色的方格中有1个方格为棋盘中心格时，共有12种染法；

(2)当中心方格未染色，但染成黄色的2个方格关于中心对称时，也有12种染法；

(3)当染成黄色的2个方格不属于以上2种情况时，有48×46÷2÷4=276种染色法.

综上所述,共有12+12+276=300种染色法.

6 制造“抽屉”分类

例6求证：从任意n个整数a1，a2，…，an中，一定可以找到若干个数，使它们的和可被n整除.

证明考察如下的n个和:

a1，a1+a2，…，a1+a2+…+ak，…，a1+a2+…+an.

若其中至少有1个能被n整除，则结论成立.

若其中没有1个能被n整除,则将他们按模的剩余类至多可分为余数为1，2，…，n-1的n-1个类.因此,这n个整数中至少有2个整数a1+a2+…+ak和a1+a2+…+ak+…+al(l>k)对模n有相同的余数.这时,和数

ak+1+…+al=(a1+a2+…+ak+…+al)-

(a1+a2+…+ak),

显然可被n整除，即结论成立.