简述与年份2010有关的竞赛题
2010-11-23绍兴市第一中学浙江绍兴312000
● (绍兴市第一中学 浙江绍兴 312000)
简述与年份2010有关的竞赛题
●虞金龙(绍兴市第一中学 浙江绍兴 312000)
在数学竞赛中常常会出现一些与年份有关的竞赛题,可分为条件中有年份与结论中有年份这2种类型.笔者自编了如下一些与年份2010有关的赛题.
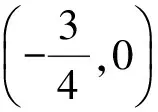
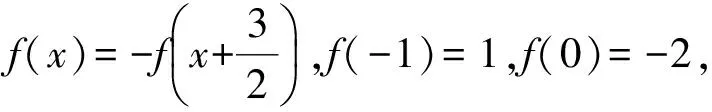
那么f(1)+f(2)+…+f(2 010)的值是________.
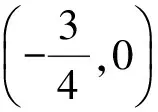
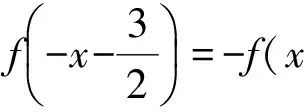
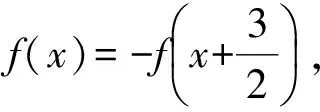
即f(x)为偶函数.因为
所以f(x)是以3为周期的函数.从而
f(1)=f(-1)=1,f(2)=f(-1)=1,
f(3)=f(0)=-2,
因此
f(1)+f(2)+…+f(2 010)=
670[f(1)+f(2)+f(3)]=0.
例2设数列{an}(n≥0)满足:

其中m,n∈N,m≥n.
(1)证明:对一切n∈N,有
an+2=2an+1-an+2;
分析(1)在已知关系式

中,令m=n,可得a0=0.令n=0,可得
令m=n+2,可得
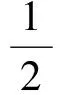
由式(1),得
a2n+2=4an+1-2(n+1),a2=4a1-2=6,
a2n+4=4an+2-2(n+2),a2n=4an-2n,
代入式(2),化简得
an+2=2an+1-an+2.
(2)由an+2=2an+1-an+2,得
an+2-an+1=(an+1-an)+2,
因此数列{an+1-an}是首项为a1-a0=2,公差为2的等差数列,从而
an+1-an=2n+2,
于是

因为

所以
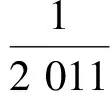
例3正整数集合的最小元素为4,最大元素为2 010,并且各元素可以从小到大排成一个公差为k的等差数列,则并集A17∪A59中的元素个数为
( )
A.119 B.120 C.151 D.154
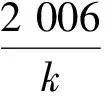
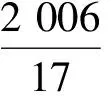
得
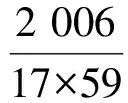
从而
|A17∪A59|=|A17|+|A59|-|A1 003|=
119+35-3=151.
例4设[x]表示不超过x的最大整数,则[log21]+[log22]+[log23]+…+[log22 010]=________.
分析当2t≤k<2t+1时,
[log2k]=t,t=0,1,2,…,
且在区间[2t,2t+1)中的正整数有2t.设f(x)=[log2x],注意到210=1 024,211=2 048,于是
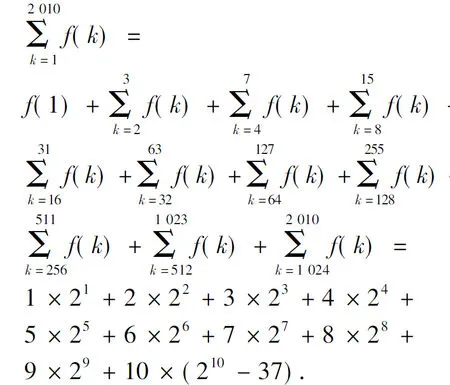
记
S=1×21+2×22+3×23+4×24+5×25+6×26+7×27+8×28+9×29+10×210,
则
2S=1×22+2×23+3×24+4×25+5×26+6×27+7×28+8×29+9×210+10×211,
从而
S=10×211-[21+22+23+24+25+26+27+28+29+210]=10×211-211+2=18 434,
因此
[log21]+[log22]+[log23]+…+[log22 010]=
18 434-37×10=18 064.
例5已知f(x)=|x+1|+|x+2|+…+|x+2 010|+|x-1|+|x-2|+…+|x-2 010|(x∈R),且f(a2-3a+2)=f(a-1),则a的值有
( )
A.2个 B.3个 C.4个 D.无数个
分析由题设知f(x)为偶函数,则考虑当-1≤x≤1时,恒有
f(x)=2×(1+2+3+…2 010)=2 011×2 010.
于是当-1≤a2-3a+2≤1,且-1≤a-1≤1时,恒有
f(a2-3a+2)=f(a-1).
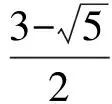
f(a2-3a+2)=f(a-1).
故选D.
