异径挤压三通应力的有限元分析

苏厚德, 冯玉洁, 樊建领

(1.甘肃蓝科石化高新装备股份有限公司,甘肃兰州 730050;2.兰州理工大学,甘肃兰州 730050)

异径挤压三通应力的有限元分析

苏厚德1, 冯玉洁1, 樊建领2

(1.甘肃蓝科石化高新装备股份有限公司,甘肃兰州 730050;2.兰州理工大学,甘肃兰州 730050)

应用ANSYS分析软件对内压作用下大异径挤压三通进行了应力计算和分析,得到了该三通模型的应力分布规律的数值结果,用理论计算结果验证了有限元分析结果的可靠性,给出了挤压三通肩部转角半径大小对三通强度的影响。结果表明,三通在主支管相贯处应力集中程度很高;当外转角给定时,最大应力与内转角近似成二次曲线关系。根据计算结果及相关文献,提出了计算挤压三通最大应力的经验关联式。

挤压三通; 有限元法; 应力分析

三通是石化天然气工业中的一个重要的连接管件。工业上常采用铸造、焊接等方式制作三通,近年来,挤压三通以其独有的优势越来越多的被采用[1]。关于三通等管道元件的应力分析的研究无疑具有重要的理论意义和应用价值,因此,已有大量的文献讨论过这类问题。Goodall W[2]最先讨论了在内压作用下设备开孔的应力分析,同时给出了三通,大小头等元件的应力分析,胡海龙等[3]编制了有限元程序,计算了偏心圆筒的弹塑性应力、容积残余变形率,给出了相应的变化规律;Schroeder J等[4-5]基于对M ises屈服面的近似,通过假设变形速度场具有一定的自由度,使得三通极限压力上限接近真实值,但此方法局限于支主管直径比小于0.4的情况。Junker A T[6]对实验用的焊制三通进行了弹塑性有限元分析,计算得到的极限面内弯矩与实验结果的最大误差为8%,但是讨论异径挤压三通的论文却比较少,尤其缺少可供工程设计人员参考的数据资料。由于三通结构为主支管相贯,属于结构不规则几何体,因此应力分析比较复杂,常规的数学分析比较困难,至今没有完整的强度理论解析解。通常,工程上采用极限载荷法、削弱系数法、压力面积法、等面积补强法等方法进行应力分析,这些方法都有其局限性,很难精确的判断三通结构的应力分布规律,其结果往往偏于保守[7-9]。与传统上把三通作为筒体开孔补强不同,本文采用ANSYS软件对多种异径挤压三通进行了较为全面的应力分析,给出了大量的数值结果,并与理论结果做了对比,验证了有限元解法的可靠性。由于实际工程配管设计中,目前国内外没有相应的大厚壁异径挤压三通的设计、制造标准,本文的计算结果可以为工程设计提供参考。

1 挤压三通有限元模型

采用的异径挤压三通计算模型如图1所示。结构仅承受内部均匀压力p,结构关于坐标xoy,yoz对称。为使大小头端面位移约束对过度圆弧面影响不至于太大(圣维南原理),主支管长度取相对较大值。

Fig.1 Calculation modal of extruded reducing tee图1 异径挤压三通计算模型

1.1 有限元模型

挤压模型由于采用了特殊的挤压工艺和合理的模具挤压成型,使得转角区壁厚有所增加,通过改变转角区的半径可以较好地改善其应力分布状态。考虑到结构和载荷的对称性,选取结构的1/4进行分析,有限元计算模型如图2所示。选用8节点实体单元(solid45),该单元每个节点有x,y,z三个方向的自由度,单元有塑性,徐变,膨胀,应力强化,大变形和大应变能力。能够较好的模拟三通在加载过程中的变形。

本文对六面体单元组成的支管1,转角过渡区2,及主管4进行映射网格化分,中间体3为七面体单元,划分为两个六面体后再用六面体单元映射划分网格或采用自由网格化分。得到的三通模型如图2所示。单元沿厚度方向分为3层,共计3 483个单元,1 595个节点。

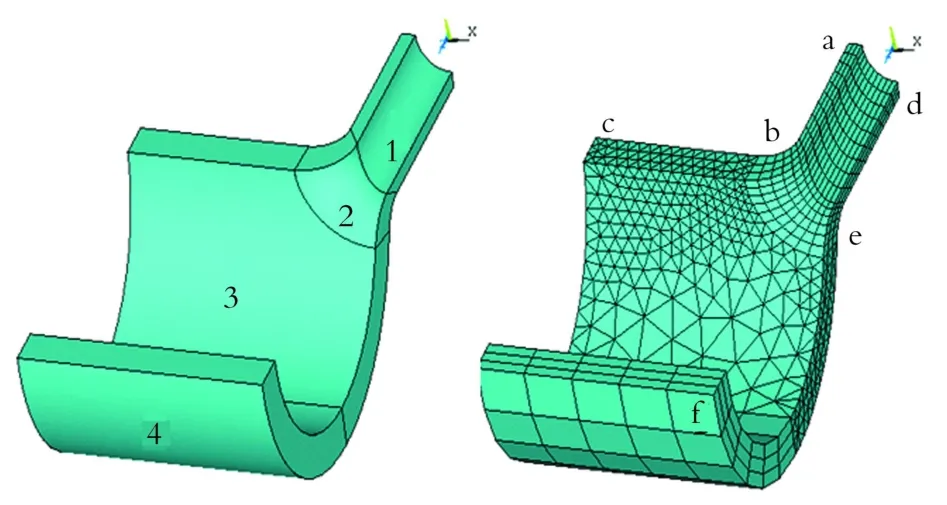
Fig.2 Finite elementmodal of extruded reducing tee图2 异径挤压三通有限元计算模型

1.2 边界条件

在结构的对称面上施加对称约束,在主、支管端面施加固定约束,内表面施加均布载荷p,这样就得到了约束充分的有限元模型。假设材料为理想的弹塑形材料,采用Von M ises屈服准则对Q235材质、管件壁厚采用sch160的挤压三通进行应力分析。

1.3 模型的有效性验证

为了考察有限元计算结果的可靠性,将本文的计算结果与文献[7-8]的计算结果进行了比较。选取的主支管尺寸为:D1=60,D=219,T1=9,T2= 23,R1=10,R2=12,单位为mm,内压p=12 M Pa,计算结果的比较见表1,可以看出文献[7-8]的计算结果偏于保守,当把内外倒角退化到0,本文的计算模型可以理解为不带补强的异径焊制三通,并与相同条件下的文献[9]做了对比,见表1,两者的计算结果相吻合,由此可以看出本文的挤压异径三通的计算模型是可靠的。

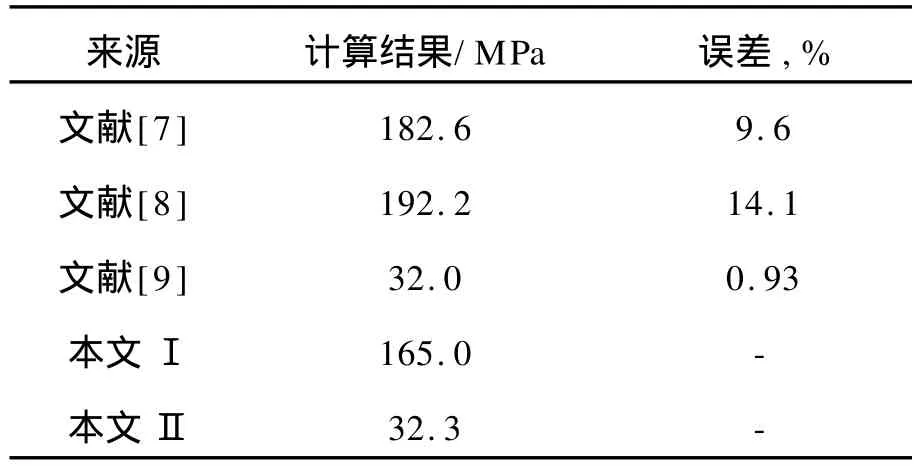
表1 本文计算结果与相关文献的比较Table 1 Results were verified in corresponding reference documents

2 结果与讨论

2.1 主支管对三通主应力的影响

首先考察了相同压力(p=12 M Pa),相同过渡区倒角(R1=10 mm,R2=12 mm)下,不同主支管尺寸对应的最大主应力,这里选用的三通壁厚是ASM E标准中sch160的管件壁厚,其结果如表2所示。

从表2中可以看出,主管尺寸一定的情况下,随着支管尺寸的增加,其最大应力随之增大;而在支管尺寸一定的情况下,随着主管尺寸的增加,其最大应力没有规律,但可以得出一些应力相对较小的主支管组合。

2.2 内压与最大应力之间的关系

给定主管尺寸26.67 cm,支管尺寸6.67 cm,过渡区倒角R1=10 mm,R2=12 mm,图3给出了多个内压所对应的最大主应力值,可以看出均布内压p与最大主应力为线性关系[10-11],而实际情况中,当p>20 M Pa时,材料变形已经进入塑性阶段,弹性应力应变关系已经不再适应,应重新进行挤压三通的塑性分析才能得到其应力峰值。具体请参见文献[12]。

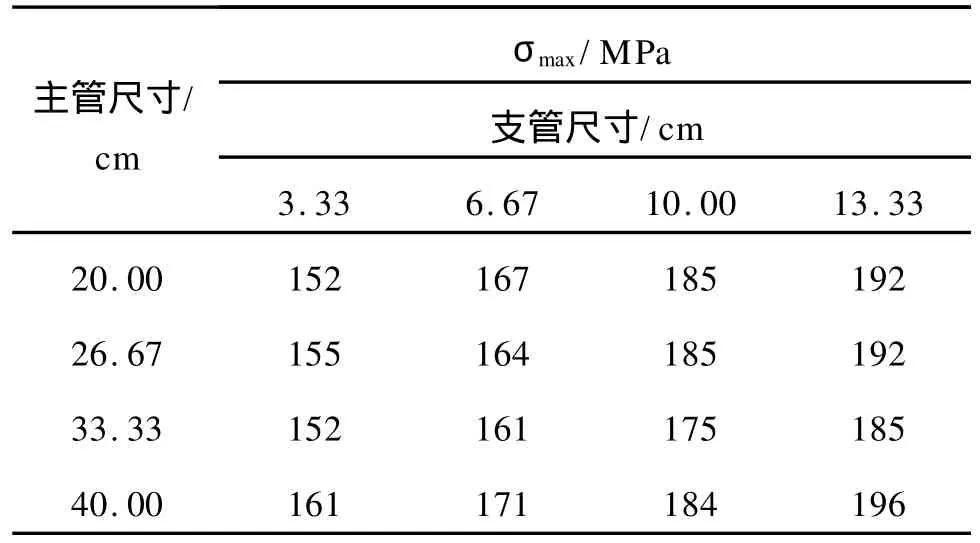
表2 不同主支管尺寸对应的挤压三通主应力值σmaxTable 2 Different pipe sizes versus themax stressσmaxof extruded reducing tee

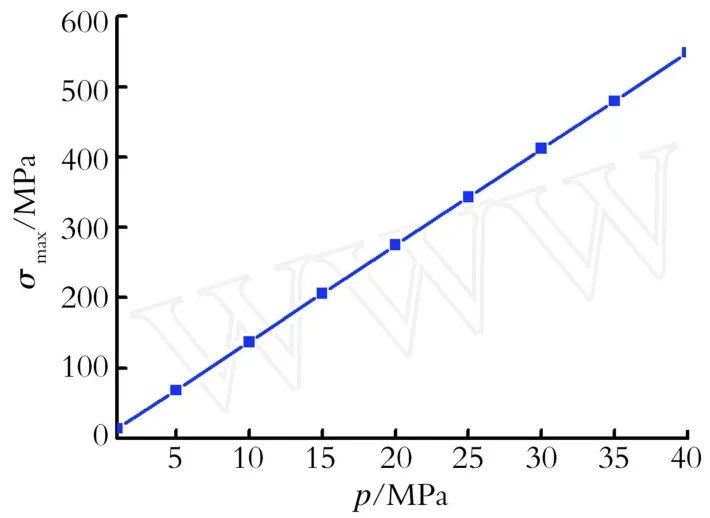
Fig.3 The linear relation between internal pressureand themax stress图3 内压与最大应力之间的线性关系

2.3 过渡区倒角与最大应力之间的关系

图4考察了过渡区倒角对挤压异径三通的影响。从图4中可以看出,当给定内压及主支管尺寸时,异径挤压三通的最大应力取决于过渡区的倒角尺寸。过大的过渡区转角将使高应力区的范围及应力值增大。当R1一定时,最大应力与R2近似成二次曲线关系,曲线的最低点为应力最小值。当R2> 5且给定时,随着R1的增大应力相应减小。因此在加工工艺允许的条件下,应尽量控制内壁转角在10～30 mm,外转角半径应尽可能的大[13-15]。

2.4 大异径挤压三通应力分布

在同压力、同过渡区倒角及同主支管尺寸情况下,图5给出了三通沿轴向abc内外壁应力变化及三通支管方向def内外壁应力变化。从图5中可以看出,三通上各点的应力随其在管壁的位置不同而不同,在远离相贯处,应力分布基本和直管段相同,由于三通结构在过渡区产生波动,应力相应发生波动,产生较大的应力梯度,在其肩部b点和腹部e点出现应力峰值,这两个部位为危险部位,而且三通的内壁峰值应力比外壁大,肩部应力峰值比腹部大,其肩部最大应力约为直管段的6倍左右[10]。

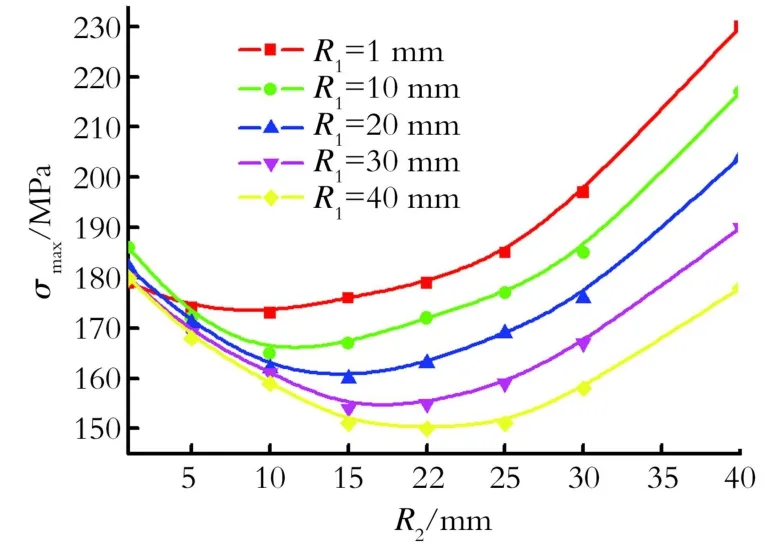
Fig.4 Radius in the transition region versus thestrength of the extruded reducing tee图4 过渡区倒角对挤压三通强度的影响

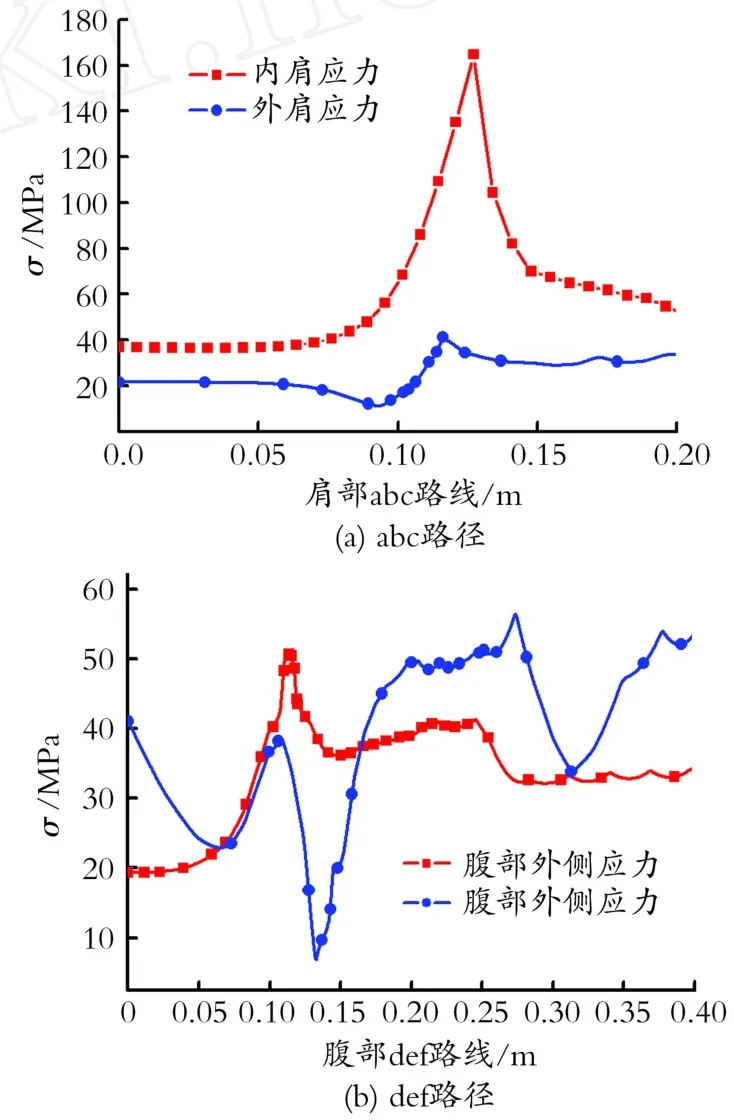
Fig.5 The stress curve along different routineof the extruded reducing tee图5 三通不同路径内外壁的应力变化

2.5 经验关联式

在本文的计算结果及相关文献[7-11]的基础上提出了计算挤压三通最大应力的经验关联式:

其中K为应力集中系数;R,Rn为主支管内半径; Rm,Rnm为计算半径;t,tn为主支管厚度;As为有效计算面积。

参考文献

[1] Yahiaouik,Moffat D G,Mo reton D N.The collapse behavio r of a fo rged piping branch junction under internal p ressure [C]//Ninth international conference on p ressure vessel technology.Sydney Australia:[s.n.],2000:155-166.

[2] Goodall W.On the design of intersection in p ressures vessels[D].London:University of Cambridge,1967:101-119.

[3] 胡海龙,闫慧菊.偏心圆筒弹塑性应力有限元分析[J].石油化工高等学校学报,1995,10(4):47-51.

[4] Schroeder J,Roy B K.Upper bounds to limit p ressures of branch-pipe lateral connections.part 1:bound fo r branch/ pipe diameter ratios smaller than 0.7[J].ASM E paper No.71-PVP-43,1971,33-39.

[5] Schroeder J,Rangarajan P.Upper bounds to limit p ressuresof branch pipe tee connection[C]//Proceedingsof the first international conference on p ressure vessel technology,part 1.New York:[s.n.],1969:171-176.

[6] Junker A T.Finite element determination of the limit load for a nozzle in a cylindrical vessel under internal p ressure[J]. ASM E paper,No.82-PVP-10,1982:19-26.

[7] Rodabaugh EC,Moore S E.Stress indices and flexibility facto rs fo r nozzles in p ressure vesselsand piping[J].NUREG/ CR-0778,1979,1:6-13.

[8] 王志祥,梁志钊,孙国模,等.管道应力分析与计算[M].北京:水利水电出版社,1983:36-45.

[9] 杨宁祥,李惠荣.异径焊制三通应力的有限元分析[J].化工装备技术,2006,27(5):25-27.

[10] Mackenzie D,Boyle J T.A simp lemethod of estimating limit loads by interative elastic analysis I simp le examples[J]. Pres.ves.piping,1993,53(5):77-95.

[11] 轩福贞,李培宁.工业压力管道三通塑性极限载荷工程分析方法[D].上海:华东理工大学,2002.

[12] 李永生,杨林娟.挤压三通强度研究[J].压力容器,1990,7(5):6-12.

[13] 轩福贞,李培宁,刘长军,等.等径挤压三通强度分析工程方法[J].设计与结构,2000,17(5):30-33.

[14] Robinson M.Lower bound limit p ressure of a flush radial cylindrical branch in a cylindrical p ressure vessel[J].Pres. ves.piping,1975,6(3):1-6.

[15] Li Shi-rong,Su Hou-de,Cheng Chang-jun.Free vibration of functionally graded material beams w ith surfacebonded piezoelectric layers in thermal environment[J].Applied mathematics and mechanics:English edition,2009,30 (8):1-14.

(Ed.:W YZ,Z)

Finite Element Analysis of Extruded Reducing Tee

SU Hou-de1,FENG Yu-jie1,FAN Jian-ling2
(1.Lanpec Technologies L im ited,Lanzhou Gansu 730050,P.R.China; 2.Lanzhou University of Technology,Lanzhou Gansu 730050,P.R.China)

19 A pril 2010;revised 19 M ay 2010;accep ted 11 July 2010

The calculation and analysis for extruded reducing tees subjected to internal p ressure were carried out using ANSYS softw are.The stress distributions law about the tee were obtained,and verified in com bination w ith the co rresponding references.The results show that the fillet radiuses have apparent effectson the tee strength.A high stress concentration crops up in the corner,and a quadratic curve relation between themaximum stressand inner radiusappearsw hen the outer radiuswas given.Based on the results and related documents,empirical co rrelation fo r calculating themaximum stressof the extruded tee is put forward.

Extruded reducing tee;Finite elementmethod;Stress analysis

.Tel.:+86-931-7639690;fax:+86-931-7639680;e-mail:suhd@lpm ri.com

TQ055

A

10.3696/j.issn.1006-396X.2010.03.020

1006-396X(2010)03-0086-04

2010-04-19

苏厚德(1979-),男,山东青岛市,工程师,硕士。

甘肃省自然科学基金项目(0803RJZA 011)。