平面压痕开裂极限临界载荷与开裂角

谢禹钧, 王 伟, 王晓华, 蔡永梅

(辽宁石油化工大学机械工程学院,辽宁抚顺 113001)

平面压痕开裂极限临界载荷与开裂角

谢禹钧, 王 伟, 王晓华, 蔡永梅

(辽宁石油化工大学机械工程学院,辽宁抚顺 113001)

平面压痕的开裂在材料机械性能的研究、破岩机理的研究中有着广泛的应用。当刚性压头作用在半平面弹性体的表面时,会产生一个平面压痕,该压痕的两端将出现I型奇异压应力场,该奇异应力场的应力集中达到一定程度时,即达到临界条件时,该奇异应力场所在的边界将开裂。压痕边界的开裂问题是一个新型的断裂力学问题,通过边界移动的能量释放率的分析定量地给出了平面压痕边界开裂能量释放率数学表征,给出了边界开裂的极限临界载荷和临界开裂角。

断裂力学; 接触力学; 应力强度因子; 压痕开裂

平面压痕开裂问题实际上是特殊的接触力学问题,即刚性压头作用在半平面弹性体的边界上,形成一个平面压痕,即研究压痕边界开裂问题。与其它类型的压头不同,在平面压痕的边缘会产生一个I型奇异压应力场,该应力场的分布与奇异性与I型裂纹裂尖应力场的奇异性相同,两类问题的奇异应力场应力集中程度均可由渐进应力场的应力强度因子来表示。弹性体中出现奇异应力场时,如裂纹问题,必然导致断裂。文献[1]给出了理想光滑边界平面压痕的开裂问题,本文将讨论边界开裂极限条件下的临界载荷上界和开裂角的下界,以下各节将给出详细的分析过程。

1 边界移动的能量释放率

本节将给出边界移动能量释放率的定义。如图1所示,对于边界S+s包围的二维弹性体,其中边界s为自由边界,S边界上作用有外力。令s边界是“时间变量t”的函数,如果s产生一个位移u,不难得出其单位时间内边界移动的能量释放率∂Π/∂t为[2-4]:

其中,w为应变能密度;vi表示速度;mi是边界s上的外向单位法矢量。

如果令vi=ei=Δi/Δ表示单位位移在坐标方向上的分量,即e1=cosα,e2=sinα,α为位移Δ与x1的夹角。若引进ni=-mi表示路径s内法线单位向量,即代表边界向弹性体内部方向移动。于是边界移动的能量释放率可定义为:

如果边界s上的各点均以同一个方向运动,如图2所示,(2)式可由守恒积分Ji表示[1],即

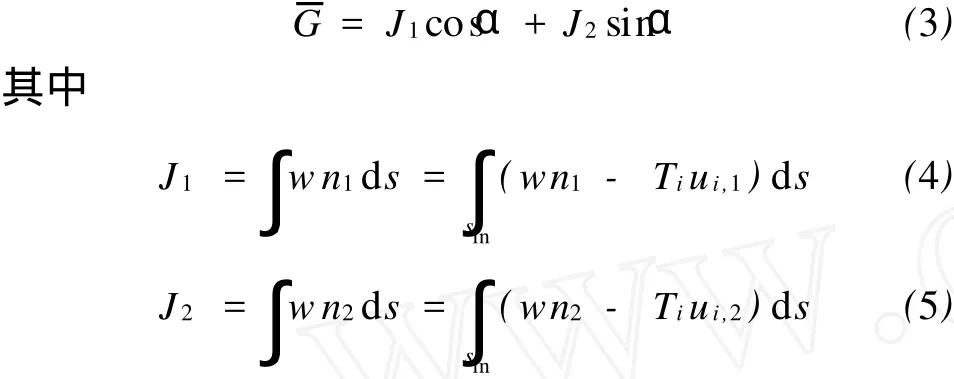
式中,sin为弹性体内的积分路径,且路径s+sin构成一个闭合路径。

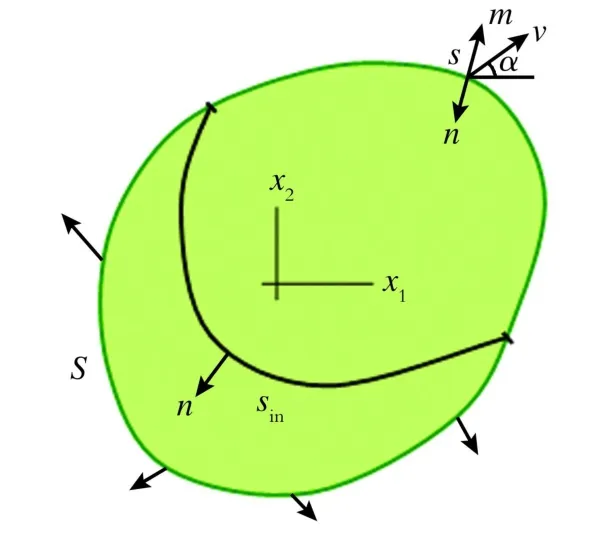
Fig.1 Two-dimensional deformation fields and in tegration path图1 二维弹性体和积分路径

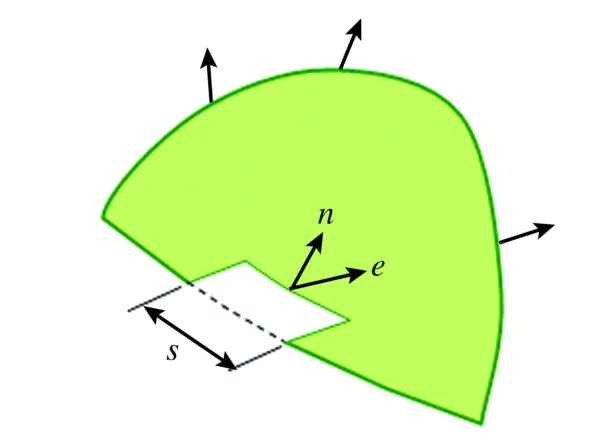
Fig.2 Model of boundary cracking when s→0图2 s→0时边界开裂模型

2 边界开裂的能量释放率

从几何观点看,边界开裂,无论发生在压痕边界还是在裂纹尖端,均为图2和图3中s→0条件下的边界移动。于是边界开裂的能量释放率可定义为[1]:

当极限存在时,(J1)|s→0表示x1方向的边界开裂驱动力;(J2)|s→0为x2方向的边界开裂驱动力。

3 极限开裂角和临界载荷

3.1 半平面弹性体平面压痕的应力强度因子

半平面触压问题如图4(a)所示,泊松比μ。刚性平端压头宽为2 l,作用在压头上的载荷为P。压痕表面压应力分布的经典解为[5]:

该应力的分布特征与图4(b)裂纹韧带裂尖近场的应力场相同。因此基体近表面压头角点处的渐近应力场为[5]:

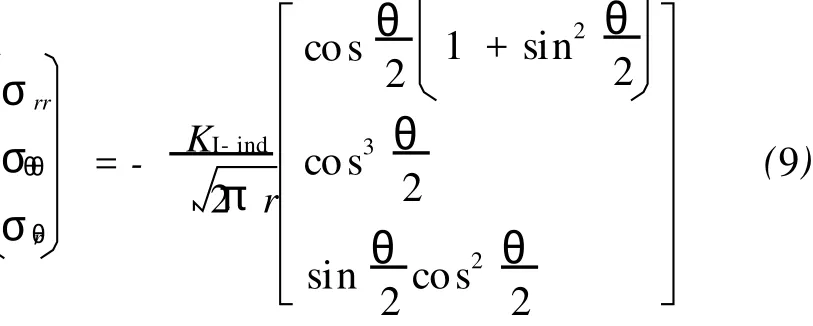
该应力场为奇异压应力场,比照裂纹问题,其中KI-ind定义为基体近表面压头角点处的奇异应力场的应力强度因子,或压痕边缘处奇异应力场的应力强度因子,表示为:

与裂纹情形相比较,(9)式给出的应力场的奇异性与裂尖同阶,只是符号相反,即I型压应力场,其应力强度因子为这一应力场强度的唯一度量,是描述触压表面近场的关键参量。如同裂纹问题一样,压痕角点表面近场存在K-控制区。

3.2 半平面弹性体平面压痕边界的开裂

理想光滑边界的平面压痕的边界开裂问题在文献[1]中已经讨论过。本节将讨论一种极限情况下的边界开裂问题,即假设在压痕边缘的角点外侧,存在一个无穷小的几何缺陷,如图5所示。这种缺陷模型在实际结构中是可能存在的,代表了一种不光滑,因此具有实际意义。

首先,计算(6)式中的J1|soa→0。令(4)式中的s =soa,如图3、5、6所示。于是在路径soo′上Ti=0和n1≠0,于是有[6]其中,sin=socba如图3、5、6所示。在此基础上,不难得出

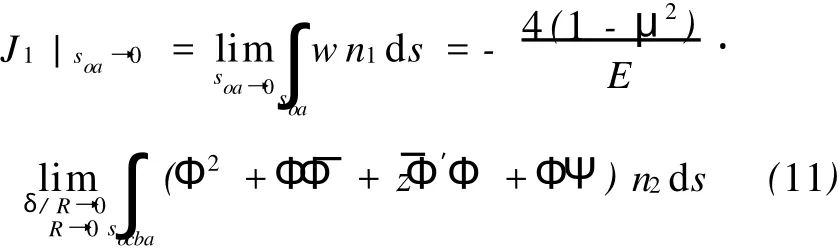
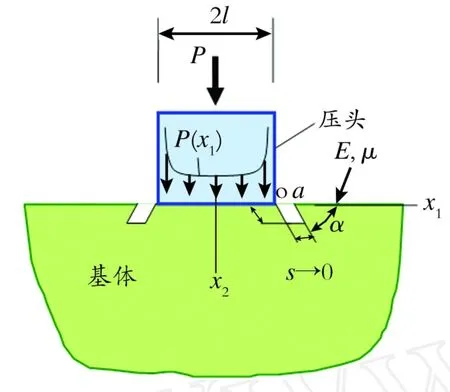
Fig.3 Boundary translation and crack embryo图3 压痕边界的移动与开裂

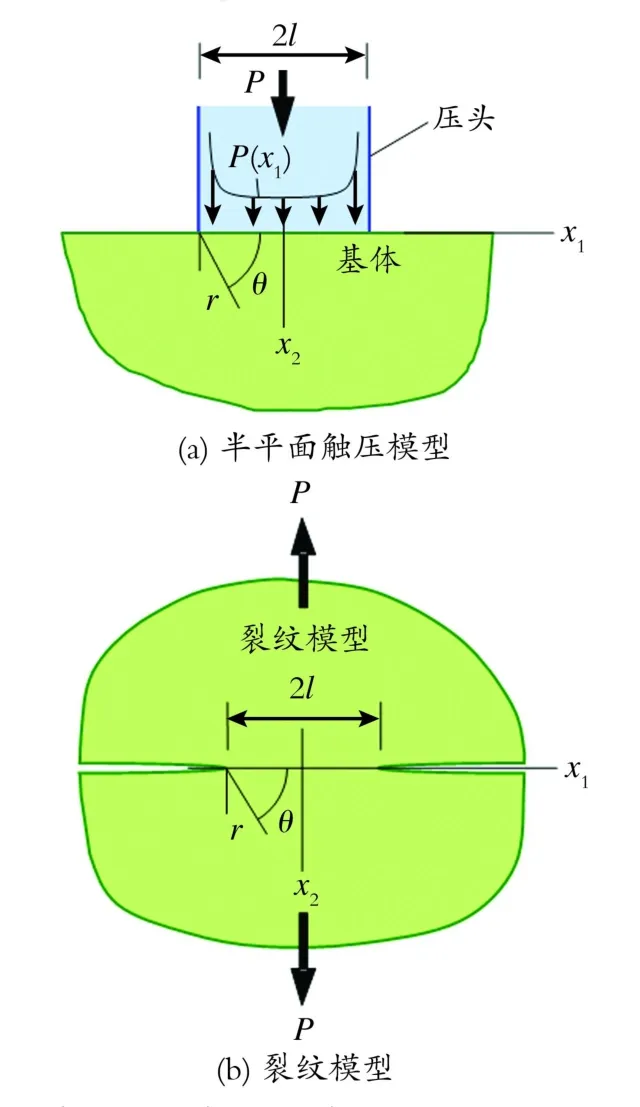
Fig.4 Half-plane indentation problem and crack model图4 半平面触压问题与裂纹模型

Fig.5 Integration pathsadjacent to right punch corner图5 压痕边缘的积分路径进而由(6)式得压痕边界沿α角开裂的能量释放率为:其中的αc为压痕边界开裂最大能量释放率所对应的开裂角,即为临界开裂角。对照文献[1]的研究结果,该临界值表现为平面压痕开裂角的下界,对应最大的能量释放率G为:

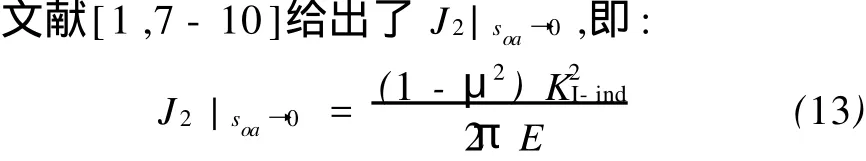
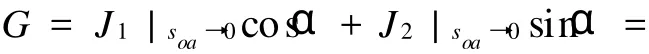
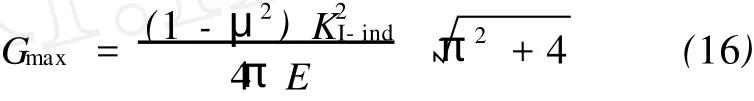
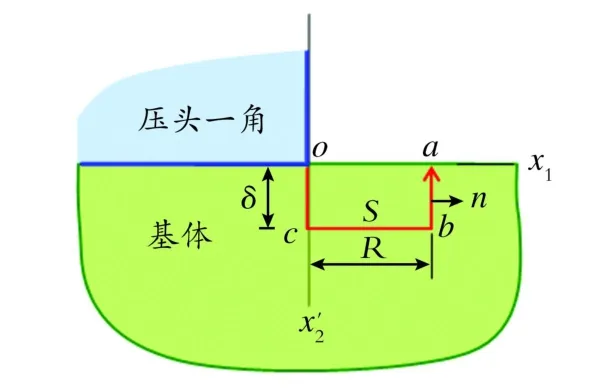
Fig.6 Integration path adjacent to punch cornerwithin the K-dom inant region图6 K-控制区内的积分路径

按照Griffith’s理论[11],弹性固体产生新的断裂表面所需要的能量来自弹性体的能量释放。Griffith’s理论给出的临界载荷为最小的边界开裂载荷,开裂方向为最大能量释放率的方向。当压痕沿αc=arctan(2/π)开裂的能量释放率达到临界值即开裂韧性Gc时,边界将开裂,即

如果将压痕边界开裂所需的能量理解为与裂纹开裂的情形相同,即为裂纹扩展的断裂韧性,进而可以给出K-型临界开裂条件:

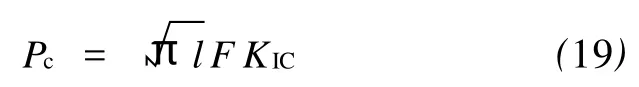
类似的,已知载荷条件下压痕开裂的临界压头宽度,即:

4 结 论

文中给出了一个压痕极限开裂的研究方法,建立了半平面压痕开裂的K-型临界开裂条件,导出了临界开裂角和临界载荷。指出压痕边界极限开裂的临界应力强度因子为裂纹开裂的4 1+4/π2倍。

更为重要的是,本文结论可以直接应用于超硬工件的超高速磨削技术、岩石切割工具的设计以及新的材料断裂韧性微创检测技术研究等。

[1] Xie Y J,Hills D A.Quasibrittle fracture beneath a flat bearing surface[J].Engineering fracture mechanics,2008,75: 1223-1230.

[2] Sih G C.Dynamic Aspectsof crack aspectsof crack p ropagation:Inelastic behavio r of solids[M].New York:M c-graw -hill book,Co.,1969:607-639.

[3] Budiansky B,Rice J R.Conservation law s and energy-release rates[J].ASM E J.appl.mech.,1973,40:201-203.

[4] Eshelby J D.The fo rce on an elastic singularity[J].Phil.trans.roy.soc.London ser.A,1951,244:87-112.

[5] Nadai A I.Theory of flow and fracture of solids[M].New York:M cgraw-hill book,Co.,1963.

[6] Cherepanov G P.Mechanicsof brittle fracture[M].New Yo rk:M cgraw-hill international book Co.,1979:266-269.

[7] Xie Y J,Xu H,Li P N.Crack mouth w idening energy-release rate and its applications[J].Theo rl.app.fract.mech., 1998,29:195-203.

[8] Xie Y J.A theo ry on cracked pipe[J].Int.j.p ressure vessels and piping,1998,75:865-869.

[9] Xie Y J,Zhang X,Wang X H.An exact method on penny-shaped cracked homogeneous and composite cylinders[J]. Int.j.solids and struct.,2001,38:6953-6963.

[10] Xie Y J.An analyticalmethod on circumferential periodic cracked pipes and shells[J].Int.j.solids struct.,2000,37: 5189-5201.

[11] Griffith A A.The phenomena of rup ture and flow in solids[J].Phil.trans.roy.soc.London,1921,A 221:163-198.

(Ed.:W YX,Z)

谢禹钧,男,1960年2月出生,1996年华东理工大学博士研究生毕业并获工学博士学位,教授、博士生导师,现任辽宁石油化工大学机械工程学院院长。牛津大学(Oxford University)高级访问学者、西澳大学(The University of Western Australia)Gledden高级访问学者,延世大学(Yonsei University)韩国BK-21计划客座研究员,韩国延世大学(Yonsei University)BK-21(第二期)微/纳米机械加工与力学国际学术顾问,辽宁省力学学会副理事长,辽宁石油化工大学学术委员会主任。辽宁省教育厅和辽宁省科技厅石油化工承压设备安全工程重点实验室主任。近三年分别主持了国家自然科学基金项目2项;主持省部级科研项目4项、先后主持省级重点教改项目2项;2007年获辽宁省科技进步三等奖1项、2009年获辽宁省教学成果一、二、三等奖各1项;在国际、国内各类期刊发表论文30余篇,累计EI、SCI收录20篇次;2008年应邀在韩国举办的微/纳米机械加工与力国际会议上做特约学术报告。

Critical Load and Cracking Angle fo r Flat Indentation

XIE Yu-jun,WANGWei,WANG Xiao-hua,CA I Yong-mei
(School of M echanical Engineering,L iaoning Shihua University,Fushun L iaoning 113001,P.R.China)

6 June 2010;revised 10 July 2010;accepted 15 July 2010

The indentation fracture can be used w idely in the areas including rock breakage and test of fracture toughness of materials.When an elastic half-p lane substrate is subject to indentations by a rigid,flat-ended punch,a singular stress field and K-dominant region should arise adjacent to the punch edges.When the intensification of such singular stress fields reaches its critical value,fracture w ill take place on the surface of the contact boundary.The cracking of indentation is a new type of f racture p roblem.By using the energy release rate of boundary translation the fracture of indentation has been formulized and critical load and critical cracking angle of the indentation have been found in the p resent paper.

Fracturemechanics;Contact mechanics;Stress intensity facto rs;Indentation fracture

.Tel.:+86-413-6865160;fax:+86-413-6865160;e-mail:yjxie@lnpu.edu.cn

O343.3

A

10.3696/j.issn.1006-396X.2010.03.016

1006-396X(2010)03-0068-04

2010-06-06

谢禹钧(1960-),男,江苏靖江市,教授,博士。

国家自然科学基金项目(50771052,50971068);辽宁省自然基金项目(20082188);辽宁省教育厅重点实验室项目(LS2010100)。