气动控制阀Choudhury粘滞模型分析与改进

丛 雨, 王树青, 谢 磊

(浙江大学智能系统与控制研究所,工业控制技术国家重点实验室,浙江杭州 310027)

气动控制阀Choudhury粘滞模型分析与改进

丛 雨, 王树青＊, 谢 磊

(浙江大学智能系统与控制研究所,工业控制技术国家重点实验室,浙江杭州 310027)

在现今研究气动控制阀粘滞特性中,Choudhury模型有着广泛的应用。对该模型进行分析,提出了改进的Choudhury模型,结果显示改进后的模型更好地描述气动控制阀粘滞特性。同时,给出了利用气动控制阀粘滞特性模型的参数(S,J)辨识结果,结果显示利用改进的Choudhury模型的参数辨识误差率均小于5%,而利用Choudhury模型的参数辨识误差超过5%。最后,通过实际工业生产过程实例,验证了改进模型参数辨识的有效性。

气动控制阀; 粘滞现象; 参数辨识

在流程工业过程中有大量的控制回路,其性能状况直接影响企业生产效益。根据Honeyw ell公司针对26 000多个控制回路历时2年多的跟踪调查发现,有2/3的回路控制性能不佳,其中最突出的表现为回路振荡[1]。而引起振荡的原因主要包括以下3个方面:控制器的参数整定不好;周期性的外部干扰;控制阀存在显著的粘滞作用。据统计控制阀粘滞占控制回路振荡原因中的20%～30%。因此,如何检测控制阀粘滞特性的存在与补偿,对化工、石油等工业过程的安全、稳定、高效的生产有着非常重要的意义[2-3]。

控制阀粘滞特性研究具体分为粘滞特性建模、检测、参数辨识及补偿4个方面。由于控制阀粘滞特性比较复杂,因此,对控制阀粘滞特性进行建模成为首要的任务。目前,比较成熟的气动控制阀粘滞特性模型是粘滞数据驱动模型,主要有3种:Kano模型[4]、Choudhury模型[5-6]和双层二叉树模型[7]。其中,Choudhury数据驱动模型得到广泛应用,但该模型存在一定的不足,即当控制信号变方向时以及阀位处于物理输出的上下界时,模型与实际物理过程不符。本文在分析Choudhury模型的基础上,修改了该模型控制阀状态改变时的判断条件,使得模型输入、输出的关系特性与实际气动控制阀粘滞特性一致。

气动控制阀粘滞特性的参数辨识是粘滞补偿过程中不可缺少的重要环节[8-11]。因而,本文进一步分析了Choudhury模型及其改进模型,对气动控制阀粘滞参数辨识结果的影响。最后,用一工业实际例子来验证改进模型的有效性。

1 Choudhury模型存在的问题

气动控制阀具有结构简单、使用安全、维护方便、价格低廉等特点,广泛应用于石油化工等流程工业中。气动控制阀根据输入信号大小来控制阀芯的位置,进而调节流过阀门的介质流量。阀芯的位置由阀芯和阀杆上所受各作用力的合力决定。

当控制阀性能良好时,控制阀的特性表现为线性特性[5]。但在实际工艺流程中,控制阀作为控制回路中唯一可以活动的元件,往往由于流体冲击、密封保护装置过紧、长时间处在高温环境中或流过黏稠液体等原因,阀杆与密封装置之间的摩擦力增大,从而导致阀门具有明显的粘滞现象,控制阀阀芯特性曲线如图1所示。

Fig.1 Behaviour of a stiction valve图1 控制阀阀芯特性曲线

由图1可知,只有当控制信号克服阀杆与阀体之间的最大静摩擦力fs时,阀杆将会移动,在移动瞬间,最大静摩擦力转变为滑动摩擦力fd,由于最大静摩擦力大于滑动摩擦力,阀杆会产生跳跃,如图1中CD段所示,这种现象被称为粘滞[4-5]。

为了模拟控制阀粘滞现象,文献[4-7]分别提出了不同的阀门粘滞数据驱动模型。其中, Choudhury模型在模拟与检测辨识粘滞参数中广泛应用,其流程图如图2所示[6]。图3为不正确的阀芯位置状态。

由图2可知,当控制器输出改变方向时该模型输出并不符合实际状况;其次,阀杆初始位置不在图1工作直线l1或l2上时,模型输出存在漏洞;另外,控制器输出由不变到再次变化时,模型输出不符合实际。假设S=10,J=4,根据图3(a)所示的控制信号输入,可以得到Choudhury模型输出如图3(b)所示;根据图3(c)所示的控制信号输入,可以得到相应的阀杆位置状态图如图3(d)所示。

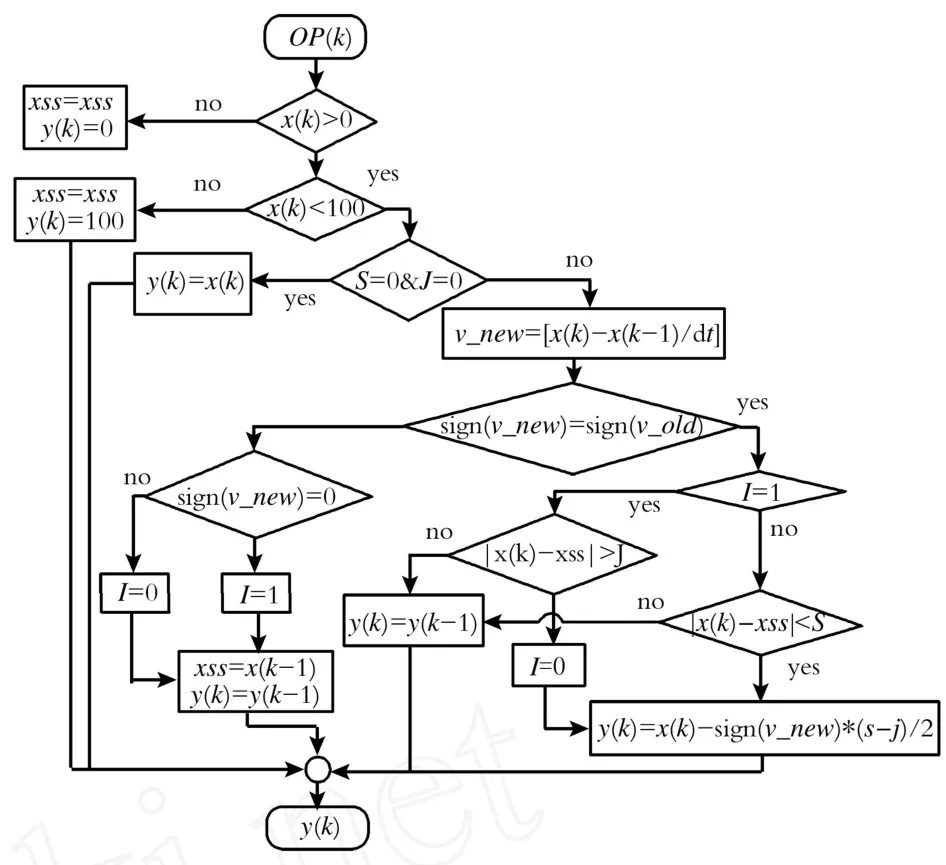
Fig.2 Logic flow chart of Choudhury model图2 Choudhury模型流程图

Fig.3 Incorrect relation between controller output and valve position图3 不正确的阀芯位置状态

图3中存在以下3个问题:①当输入控制信号的方向发生改变且变化量大于控制阀粘滞参数S时,阀杆应随之反向移动,但图3(a)中第2个采样时刻控制器输出由0跳变到50,信号变化量大于粘滞参数S,但图3(b)中输出仍保持不变,模型处于粘滞状态,不符合实际控制阀输出。同样在采样时刻4～9 s也存在类似问题;②假设阀杆初始位置为0。由于静摩擦力的存在,当控制器输出克服最大静摩擦力fs时,阀芯位置会产生相应的跳跃,而图3中(d)所示模型在控制器输出大于S(S>fs)时才产生跳跃;③控制器输出由不变到再次变化时,控制信号只需克服阀门粘滞J阀杆即可移动,而图3中(d)所示控制信号变化量为S时阀杆才开始移动,不符合控制阀实际阀门特性。

2 气动阀粘滞模型改进算法

针对上述指出的Choudhury模型存在的3个问题,本节将分别予以详细分析,并给出改进后的Choudhury模型,如图4所示。图5为修改后正确的阀杆位置状态。

(1)由上述可知,当Choudhury模型输入信号改变方向时模型输出始终保持不变。若此时的信号变化量大于反向滑动摩擦力与最大静摩擦力之和S时,控制信号将会驱动阀杆克服阻力移动, Choudhury模型输出与实际特性不符。在该情况下控制阀输出应分两种情况考虑:当信号变化量小于粘滞参数S时,阀杆处于静止状态;反之,阀杆将会移动。本文在Choudhury模型的基础上增加了输入信号改变方向情况下阀杆是否移动的判断项,同时为确保xss参数准确更新,增加了更新xss参数的判断项。在图4方块(i)中首先判断上一时刻阀杆是否移动,如果上一时刻阀杆移动,那么将xss参数置为上一时刻控制信号输出,否则xss参数不变。然后判断控制信号反向时信号变化量是否满足阀杆反向移动的条件。如果满足,那么阀杆移动,同时将代表阀杆移动状态的参数I置为0;反之阀杆静止,参数I置为1。根据第1节中给出的粘滞参数及控制信号,修改后的模型可以得到相应正确的阀杆位置,如图5(b)所示,在时刻2～9 s,在控制器输出变化量大于粘滞参数S时,控制阀输出发生了正确改变。

(2)模型初始阀位为0时,控制器输出大于时阀杆才产生跳跃,与实际特性不符。说明当阀杆处于物理输出的上界或下界时以及初始阀位不在直线l1、l2上时,按照Choudhury模型框图编写的程序将产生错误的阀芯位置状态变化。由上述分析得知, Choudhury模型在判断阀杆是否满足由静止到移动的条件上存在错误,本文将原模型中判断条件:|x (k)-xss)|>s改为|x(k)-y(k-1)|>fs,如图4中方块(ii)所示。根据给出的粘滞参数及控制信号,修改后的模型可以得到相应正确的阀杆位置,如图5(d)所示。

(3)控制器输出由不变到再次变化时, Choudhury模型在输入信号变化量为S时阀杆产生跳跃,与实际特性不符。因为这种情况下,只有当控制器信号变化的方向与上次阀杆移动的方向相同时,控制信号克服阀杆上粘滞作用,阀杆移动,否则控制信号需满足阀杆反向移动的条件阀杆才可移动,说明Choudhury模型在判断控制阀是否满足同向移动的判断条件上存在错误。因此,需要添加针对控制器信号变化是否与上次阀杆移动同向的判断条件。为实现以上逻辑判断,本文设置一个新的变量d v,用来代表上次阀杆移动的方向。根据粘滞特性以及图1所示的控制器输出与阀芯位置关系规则,令d v=sign(xss-y(k-1)),判断d v和v_new是否同向。如果满足判断条件,那么控制信号变化量只需克服粘滞作用J即可使阀杆移动,反之控制信号需满足阀杆反向移动的条件才可使阀杆移动。修改后的Choudhury模型如图4中方块(iii)所示。根据给出的粘滞参数及控制信号,修改后的模型可以得到相应的正确阀杆位置状态如图5(d)所示。

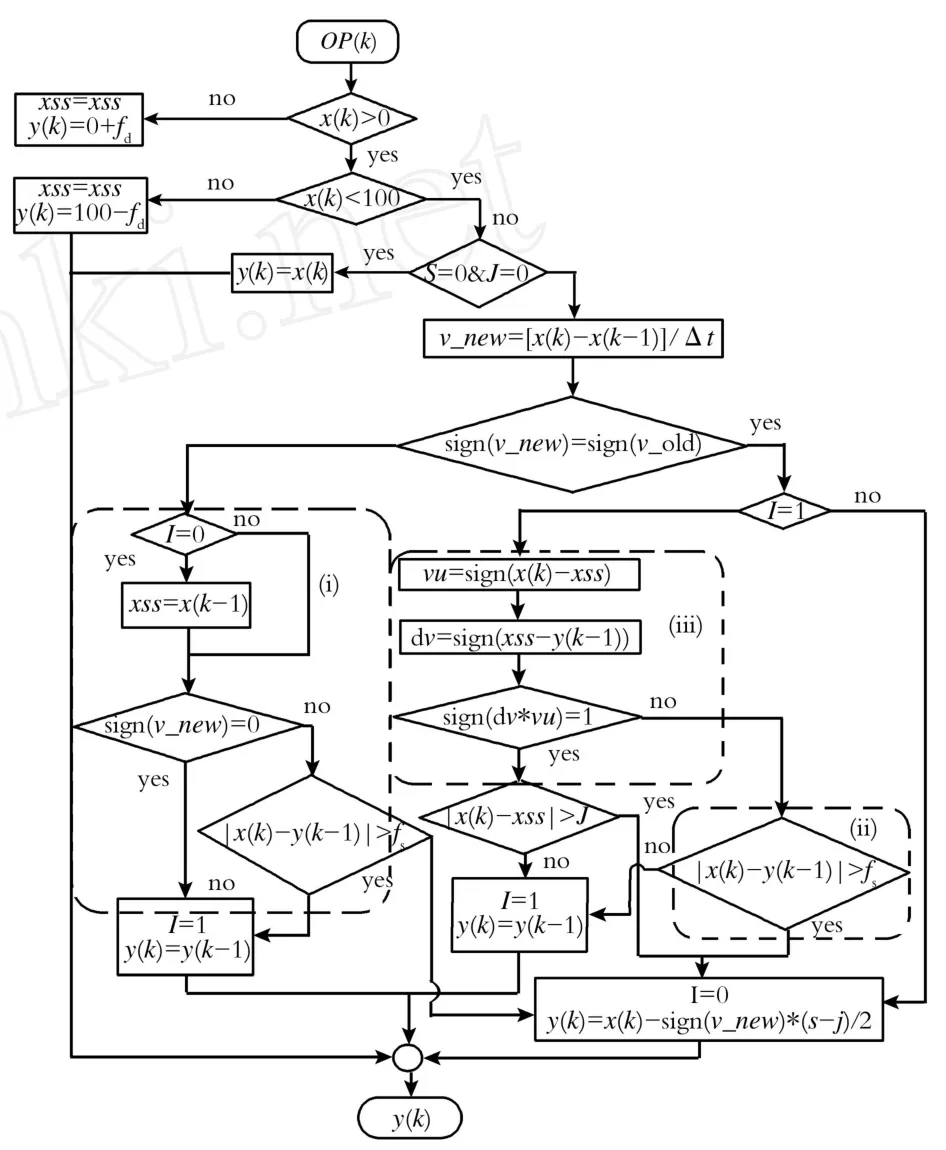
Fig.4 Logic flow chart of the improved Choudhury model图4 修改后的Choudhury模型的流程图

3 模型对粘滞参数辨识的影响

3.1 粘滞参数辨识方法原理与算法

控制阀粘滞特性研究是通过检测回路中控制阀粘滞特性的存在,以及对粘滞参数的辨识,最终实现粘滞补偿,达到减小回路振荡的目标。本文采用的是第2节中改进的Choudhury模型。由于生产过程的对象模型往往未知,因而辨识气动控制阀粘滞参数的同时需要对过程对象模型进行联合辨识。为简化问题,假设过程对象模型为线性,回路可分解为非线性部分和线性部分,利用Hammerstein模型辨识可同时描述出阀门粘滞参数和过程对象模型,并通过最小方差法求相对应的粘滞参数。由此粘滞参数辨识问题可转化为求方差最优解,如式(1)所示。

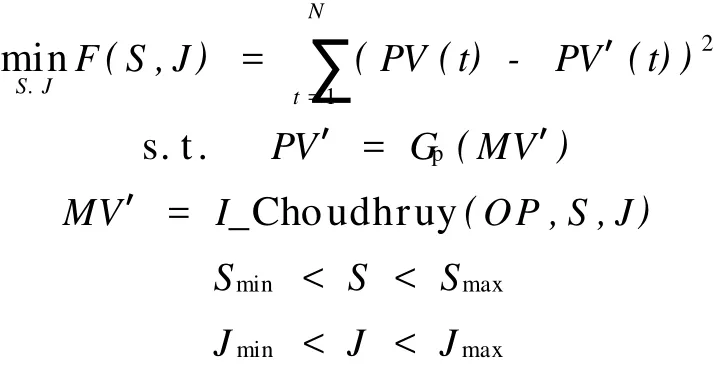
其中,S,J为粘滞参数,O P、PV分别为回路中控制器输出和被控变量输出,M V′为相应模型输出,PV′为预测输出,Gp为被控对象传递函数,I_Choudhury (.)为图4中改进后的Choudhuary控制阀数据驱动模型。

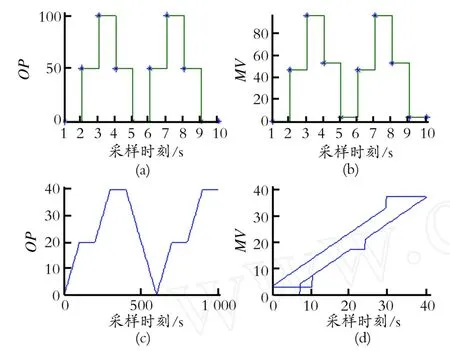
Fig.5 Correct relation between controller output and valve position图5 正确的阀杆位置状态

由于控制阀粘滞特性为非线性特性,一般无法采用基于目标函数梯度的优化算法来求解,因此通常采用演化算法(如遗传算法)来解决此问题[6,9-11]。微粒群优化算法(PSO)是由Kennedy和Eberhart于1995开发的一种基于迭代的优化方法[12],通过群体中粒子间的合作与竞争产生的群体智能指导优化搜索。由于PSO算法简单,易于实现,具有较强的全局收敛能力,近年得到了很大的发展,十分适合解决此问题。因此本文采用基于PSO算法的粘滞辨识算法。

基于PSO控制阀参数辨识算法的粒子适应度计算如下:

(1)Hammerstein模型中非线性部分为控制阀粘滞部分,用改进的Choudhury模型来描述,回路线性部分为控制阀线性部分及过程对象,该线性部分可利用ARX或ARMAX模型来描述;

(2)二维取值范围内选择一组;

(3)根据参数为(Si,Ji)的粘滞模型及控制信号OP可得到相应的阀芯位置MV′;

(4)利用阀芯位置M V′和过程输出PV数据辨识过程对象的模型;

(5)根据辨识出的过程对象的模型以及阀芯位置M V′可以得到过程预测输出PV′;

(6)计算预测输出PV′与实际输出PV之间的方差F(Si,Ji);

(7)计算二维取值范围内各点所对应的方差M SE,为各粒子的适应度值。

3.2 模型对参数辨识的影响

考虑单回路控制,控制对象和控制器采用文献[11]中的仿真对象及相应控制器Gc控制阀采用改进后的Choudhury粘滞模型。由于实际过程控制阀粘滞一般在1%～2%[1],所以控制阀粘滞仿真参数设置为[0,2%],对每组S,J的取值各产生了1 500个样本。为符合工业过程的真实情况,在回路输出信号上增加了方差为0.01的正态随机噪声。控制对象辨识采用ARX模型,并根据A IC准则确定模型阶次[11]。PSO算法中自身正反加速度和种群正反加速度分别设置为0.5,惯性权重设置为1.2,粒子数设置为20,最大迭代数为20。利用所提供的确定参数取法范围的方法以及微粒群优化算法得到粘滞参数辨识结果见表1。

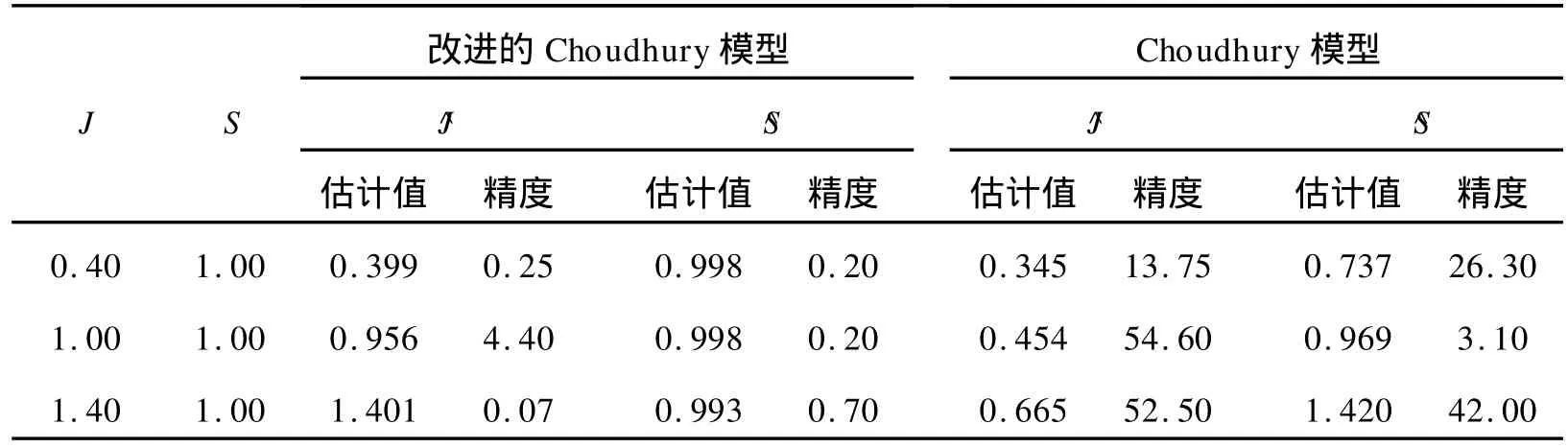
表1 粘滞参数辨识结果Table 1 Results for the process simulations%

从表1可以看出,改进的Choudhury模型的辨识精度均小于5%,而Choudhury模型的辨识精度只有一个小于5%,其余均超过5%,最大达到54.60%,与粘滞参数实际值存在较大差异。

由于粘滞模型为非线性模型,目标函数极可能存在局部最优解。从辨识结果中,并不能十分肯定地判断该辨识结果的差异是否由模型不同造成的。所以为了分析差异的原因,要从优化算法、模型差异和噪声影响这几个方面考虑。

首先,为排除噪声影响和优化算法产生的局部最优值所产生的差异,将在无噪声情况下,以表1中第1组粘滞参数为例,利用改进的Choudhury模型作为气动控制阀模型模拟闭环控制,在寻优最大范围内,以0.1%为最小精度平均划分二维网格线,求取每个网络节点所对应的目标函数值。所求取的Choudhury模型、改进的Choudhury模型对应的目标函数的三维图分别如图6中(a)和(b)所示。图中x、y轴分别为S参数和J参数,Z轴为最小方差。

从图6的(a)和(b)中可以直观看出,改进的Choudhury模型最优点在设定参数附近,而Choudhury模型所对应目标函数的三维图有明显的不同。为何会造成如此差异呢?下面将在有噪声且输入相同OP曲线情况下,针对Choudhury模型及改进模型所产生的MV、M V改进进行对比分析。

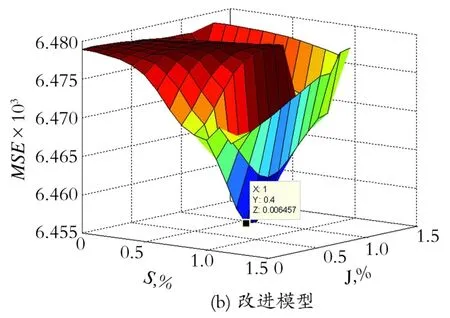
Fig.6 The objective functions of originalmodel and im proved model图6 原模型及改进模型对应的目标函数

同样,以表1中第1组粘滞参数为例,添加0.01%的白噪声,并针对过程对象FOPTD及其控制器,利用改进的Choudhury模型作为气动控制阀模型进行闭环回路控制的模拟。

回路中设定值设为常数50%。回路控制器输出信号O P和Choudhury模型及改进模型所产生的M V、M V改进曲线图,选取50 s至350 s进行局部放大如图7所示。从图7中可以看出,MV与M V改进信号在250 s至350 s之间存在明显差异。256 s时改进模型的阀杆反向移动,而Choudhury模型的阀杆仍然静止。产生此差异的具体原因需从85 s阀杆进入静止状态时开始分析。85 s时,控制信号值为1 7.0 9%,8 6 s时控制信号值仍为17.09%,因而阀杆进入停滞状态;260 s时控制信号值变为16.08%,与上次阀杆由移动到静止状态的控制信号值xss之间相差了-1.01%,其绝对值大于S,因而阀杆应产生反向移动。而Choudhury模型逻辑上存在问题,只要控制信号反向变化或保持不变时该模型就会更新变量xss。又由于噪声干扰存在,控制信号虽在100 s至250 s之间是减小的趋势,但相邻时刻的控制信号存在不变或反向情况,所以xss值不断变化。由上述分析,参数xss并不能代表上次阀杆由移动到静止状态的控制信号值,因而产生了差异。

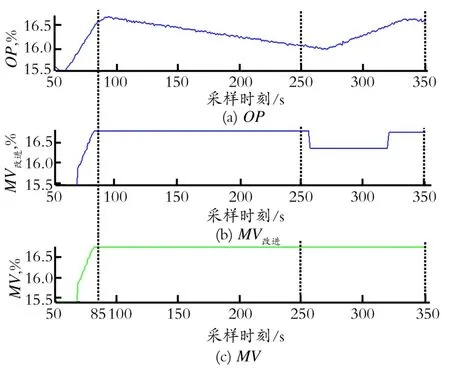
Fig.7 Partial curve of OP,MV,MV改进图7 OP及MV、MV改进局部曲线图

4 工业实例应用研究

为验证改进模型及参数辨识方法的有效性,本文采用某石化厂延迟焦化车间5个典型的闭环控制回路数据进行气动控制阀粘滞参数S,J的辨识分析。这5个回路均为流量控制系统,其中JFICA 137为控制重质渣油由缓冲罐流入加热炉F-1的总管路上流量控制回路,JFICA 0145、JFICA 0147、JFICA 0157和JFICA 0159为重质渣油流入加热炉F-3四条分管路的流量控制回路。采样周期为5s,采样时间段中包含20个震荡周期以上,采样点数分别为1 000、1 000、1 000、1 000、750。5个回路的控制器输出,控制对象输出,及PV-OP图见图8。采用辨识算法,其中PSO算法中自身正反加速度和种群正反加速度分别设置为0.5,惯性权重设置为1.2,粒子数设置为20,最大迭代数为20。最后得到这5个气动控制阀粘滞参数辨识结果如表2所示,结果显示JFICA 137回路中的气动执行阀粘滞参数分别为S=0.023%,J=0.023%,均小于0.05%,可忽略。这是由于流过的介质温度不高,因而具有较小的粘滞特性。而回路JFICA 0145、JFICA 0147、JFICA 0157和JFICA 0159主要控制炉膛F3的4个管路的进料流量,流过气动执行阀的重质渣油粘稠,含杂质多,并且温度高,压力大;从辨识结果中分析,可知4个回路的S或J参数都大于1.0%,说明这些气动控制阀有粘滞现象。因为在大量研究中,认为S或J参数大于1.0%,则认为控制阀具有粘滞特性[1]。

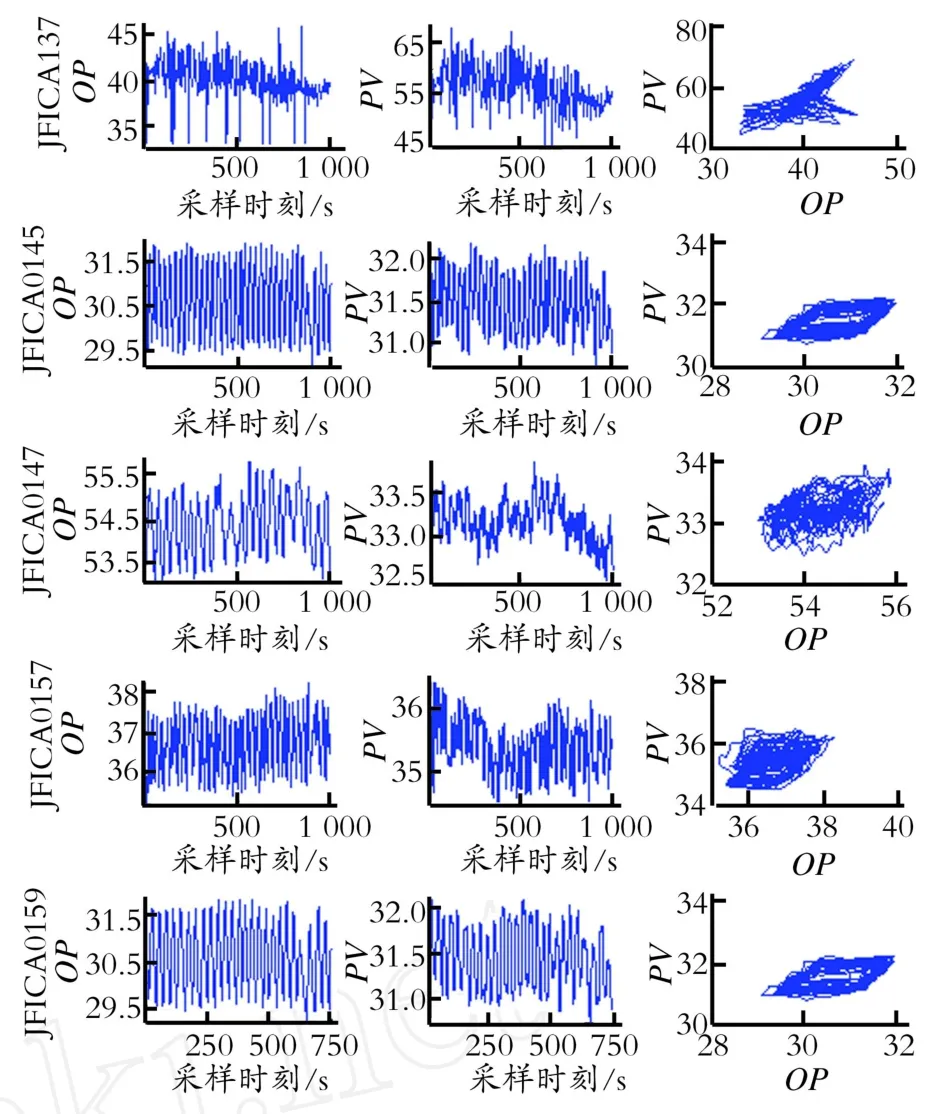
Fig.8 Industrial control loop data图8 工业数据

表2 工业实例辨识结果Table 2 Results of the industrial control loops

[1] Desbo rough L,M iller R.Increasing customer value of industrial control performance monito ring-honeywell’s experience[J].Proceedings of p rocess control,2002:172-192.

[2] Tho rnhill N F,Hagglund T.Detection and diagnosis of oscillations in control loops[J].Control engineering p ractice, 1997,5(10):1343-1354.

[3] Hagglund T.A control-loop performancemonito r[J].Control engineering p ractice,1995,3(11):1543-1551.

[4] Manabu K,Hiroshi M,Hidekazu K,et al.Practical model and detection algorithm for valve stiction[C].IFAC symposium on dynamics and control of p rocess system s,2004:5-7.

[5] Shoukat C M A A,Tho rnhill N F,Shah S L.Modelling valve stiction[J].Control engineering p ractice,2005,13(5): 641-658.

[6] Choudhury C M A A,Jain M,Shah SL.Detection and quantification of control valve stiction[C].Proceedings of the 7the DPCOPS,USA:Boston,2006:2097-2106.

[7] Si-Lu C,Tan K K,Sunan H.Two-layer binary tree data-driven model fo r valve stiction[J].Ind.eng.chem., 2008,47:2842-2848.

[8] Srinivasan R,Rengaswamy R,Narasimhan S,et al.Control loop performance assessment 2:Hammerstein model app roach fo r stiction diagnosis[J].Industrial&engineering chemistry research,2005,44(17):6719-6728.

[9] Jain M,Choundhury M A A S,Shah S L.Quantification of valve stiction[C].International symposium on advanced control of chemical p rocesses,Brazil:Gramado,2006:1157-1162.

[10] Choudhury M A A S,Jain M,and Shah SL.Stiction-definition,modelling,detection and quantification[J].Journal of p rocess control,2008,18(3-4):232-243.

[11] Jelali M.Estimation of valve stiction in control loops using separable least-squares and global search algorithm s[J]. Journal of p rocess control,2008,18(7-8):632-642.

[12] Kennedy J,Eberhart R.Particle swarm op timization[C].Neural networks,p roceedings,IEEE international conference,Piscataway,NJ:IEEE service center,1995.

(Ed.:SGL,Z)

王树青,男,汉族,1938年12月生,浙江省仙居县人,自动化方向的硕士、博士、博士后和国内外访问学者导师,现为浙江大学控制系返聘教授。曾任工业控制技术国家重点实验室主任、中国微生物学会常务理事及名誉理事、中国生物过程模型化与控制学会理事长及副理事长、中国自动化学会应用委员会(过程控制)常务理事和中国化工学会化工自动化及仪表委员会常务理事等职务。先后获得国家教育部科技进步一等奖,国家教委科技进步二、三等奖,国家计委、科委和财政部联合嘉奖等荣誉。享受国务院颁发的政府特殊津贴。主要研究方向:先进控制理论与应用,控制系统性能评估方法与应用,基于多智能体的网络控制系统理论及应用,运动控制算法及实施,企业综合自动化理论与应用。

Analysis and Imp rovement on Choudhury’s Stiction Model of Pneumatic Control Valve

CONG Yu,WANG Shu-qing＊,XIE Lei
(N ational Key Laboratory of Industrial Control Technology,Institute of Cyber-Systems and Control,
Zhejiang University,Hangzhou Zhejiang 310027,P.R.China)

20 M ay 2010;revised 9 Ju ly 2010;accep ted 12 July 2010

Choudhury’s model was w idely used in the pneumatic control valve stiction research.Based on the analysis and discussion fo r Choudhury’smodel,the results show that the imp roved Choudhury describes the characteristicsof valve stiction better.Then,the identification results of stiction parameters(S,J)were given by using the Choudhury’s model and the imp roved Choudhury’smodel.The results show that the error ratesof identification used by the imp roved Choudhury’smodel are all below 5%,w hile the erro r rates of identification used by the Choudhury’s model are over 5%.The validity of the p roposed method is illustrated through industrial examp les.

Pneumatic control valve;Stiction;Parameter identification

TP311+.32

A

10.3696/j.issn.1006-396X.2010.03.022

1006-396X(2010)03-0094-07

2010-05-20

丛雨(1984-),女,辽宁大连市,在读硕士。

国家自然科学基金(60721062);国家高技术研究发展(863)计划资助项目(2007AA 04Z162)。

＊通讯联系人。

＊Co rresponding author.Tel.:+86-571-87951125;fax:+86-571-87951125;e-mail:sqwang@iipc.zju.edu.cn