2 0 1 0年全国高中数学联赛模拟卷

第一试

一、填空题(每小题8分，共8小题，满分64分)

4.在△ABC 中，a，b，c是角 A，B，C 的对边，且满足 a2+b2=2c2，则角 C的最大值是_______.

5.设2 000=2a1+2a2+… +2an，其中a1，a2，…，an是两两不等的非负整数，则a1+a2+… +an= _______.

7.已知△ABC 的3条边长分别为13，14，15.有4个半径同为r的圆O，O1，O2，O3放在△ABC 内，并且圆O1与边AB，AC相切，圆 O2与边 BA，BC相切，圆 O3与边 CB，CA相切，圆 O与圆 O1，O2，O3相切，则 r=_______.

8.设ABCDEF为正六边形，一只青蛙开始在顶点A处，它每次可以随意地跳动到相邻两点之一，若在5次之内跳到点D，则停止跳动;若在5次之内不能跳到点D，则跳完5次也停止跳动，那么这只青蛙从开始到停止，可能出现的不同跳法共有_______种.

二、解答题(每小题12分，共3小题，满分36分)

{x|f15(x)=x，x∈［0，1］}中至少含有9 个元素.

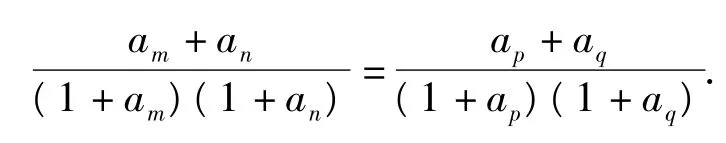
参考答案

10.解 设 A(x1，y1)，B(x2，y2)，直线 AB 的方程为y=kx+m.因为点A既在椭圆上，又在直线AB上，所以

将式(1)代入式(2)，得

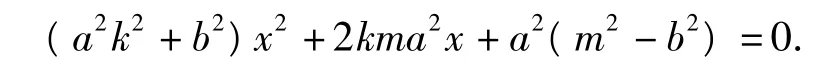
由直线与椭圆相切，可得

同理，由点B既在圆上又在直线AB上，可得

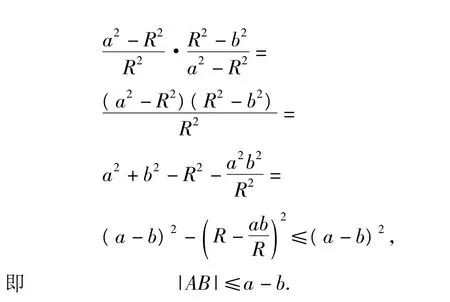
显然，λ为与a有关的常数.

第二试

一、在△ABC中，D，E，F和X，Y，Z分别为边 BC，CA，AB上的中点和高的垂足，ZD 与 FX交于点 L，ZE与FY交于点M，DY与XE交于点N，求证：点L，M，N都在△ABC的欧拉线上(即三角形外心和垂心的连线上).

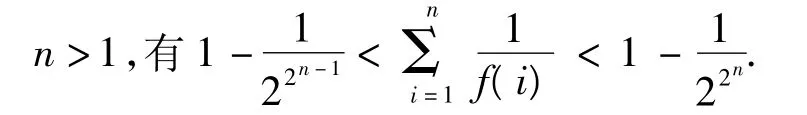
三、试确定所有的正整数组(x，y，z)，使得 x3-y3=z2，其中 y 是质数，y|/z，3|/z.

四、设M是平面上n个点组成的集合，满足：

(1)M中存在7个点是一个凸七边形的7个顶点;

(2)对M中任意5个点，若这5个点是一个凸五边形的5个顶点，则此凸五边形内部至少含有M中的一个点.

求n的最小值.

参考答案

一、证明 设点O，H分别为△ABC的外心和垂心，下面证明点L在OH上.设△ABC的外接圆半径为 R，直线ZC，FX 交于点P，连结 OF，HL，OL.由 OF⊥AB，PZ⊥AB，得

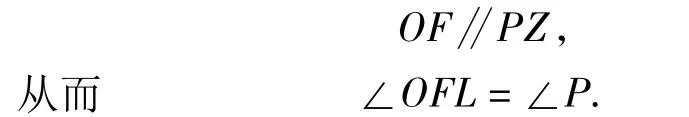
由点F为Rt△AXB斜边AB上的中点，得FX=FB，

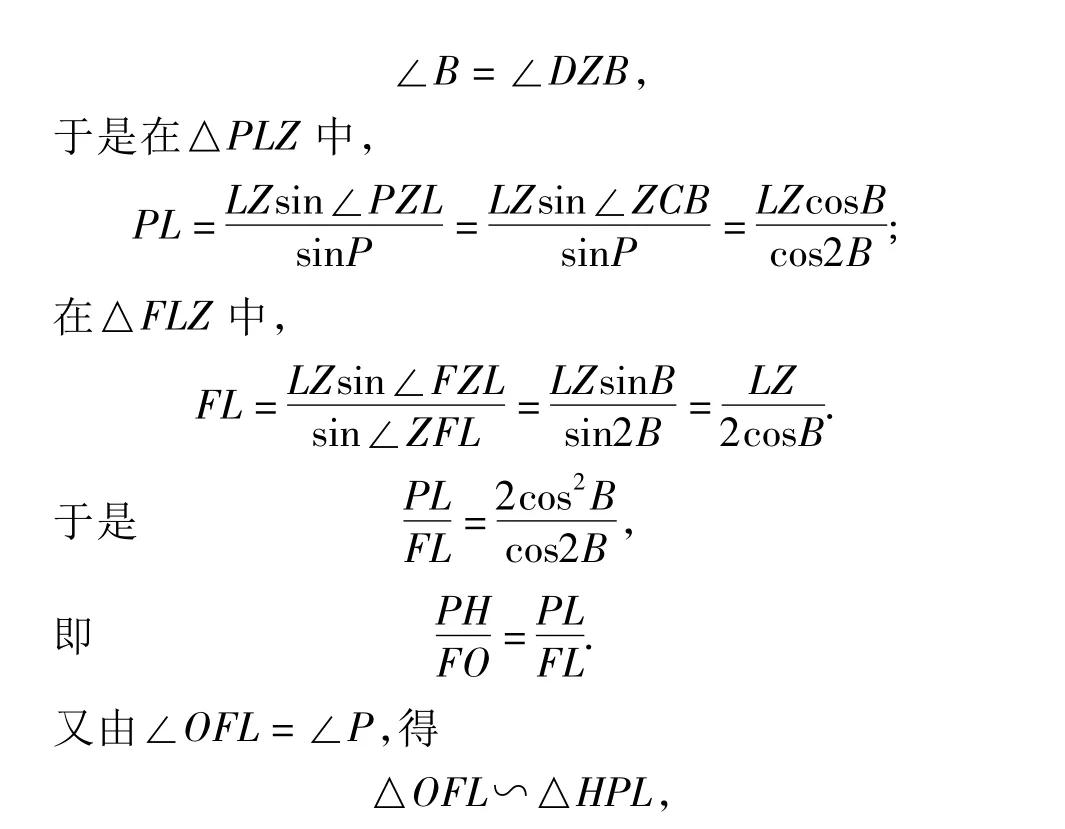
而点F，L，P共线，故点O，L，H共线，即点 L在 OH上.同理可证点M，N也在OH上.

二、解 由题设显然有f(n)≥2.将f(n+1)=［f(n)］2-f(n)+1变形为下面用数学归纳法证明式(8)对n≥2的一切整数都成立.

显然式(8)成立.假设当n=m时，式(8)成立.则当n=m+1时，有

f(m+2)=f(m+1)［f(m+1)-1］+1.(9)由归纳假设得

因为f(m+1)是正整数，所以

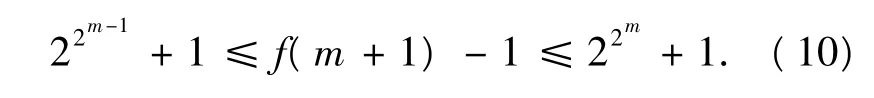
由式(9)，式(10)，得

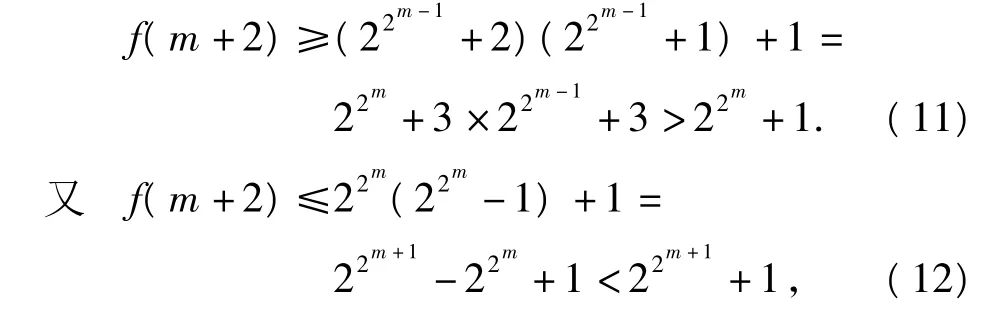
于是由式(11)，式(12)知，式(8)对 n=m+1成立.因此式(8)对任意正整数n≥2都成立.故所证不等式成立.

三、解 由题意，得

综上所述，满足条件的正整数组是唯一的，即(8，7，13).

四、解 先证：n≥11.

设顶点在M中的一个凸七边形为A1A2A3A4A5A6A7，连结 A1A5.由条件(1)知，在凸五边形A1A2A3A4A5中至少有M中的一个点，记为P1.连结 P1A1，P1A5，则在凸五边形 A1P1A5A6A7内至少有M中的一个点，记为 P2(异于P1)，连结P1P2.由抽屉原理知，在直线P1P2的某一侧必有3个顶点，这3个顶点与点P1，P2构成的凸五边形内，至少含有M中的一个点P3.

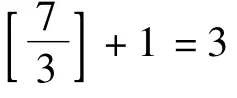
127域(不妨设为π3)中，这3个点与P1，P2构成一个顶点在M中的凸五边形，故其内部至少含M中的一个点P4，因此n≥11.

下面构造一个例子说明n=11是可取的.如图1所示，凸七边形A1A2A3A4A5A6A7为一整点七边形，其内部有4个整点，则条件(1)显然满足.这个点集M也满足条件(2).证明如下，用反证法.

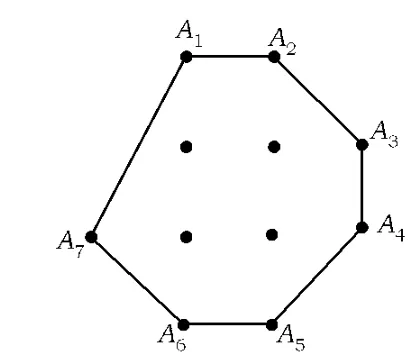
图1

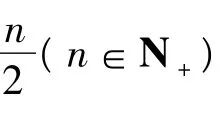
综上所述，n的最小值为11.