规范五边形重心定理

华漫天

(浙江省慈溪实验中学 315300)

众所周知，三角形三条中线交于一点，这个点称为重心，且重心到顶点的距离是它到对边中点距离的2倍.笔者发现，某些五边形具有跟三角形重心定理类似的结论.

规范五边形

如图1，五边形ABCDE中，我们把边CD称为∠BAE的对边，∠BAE则称为边CD的对角；设点F是边CD的中点，称线段AF为五边形ABCDE的一条中线；若中线AF把五边形ABCDE分成面积相等的两部分，则称中线AF是五边形ABCDE的规范中线.如果五边形ABCDE的五条中线都是规范中线，则称这个五边形是规范五边形.显然，正五边形是特殊的规范五边形.

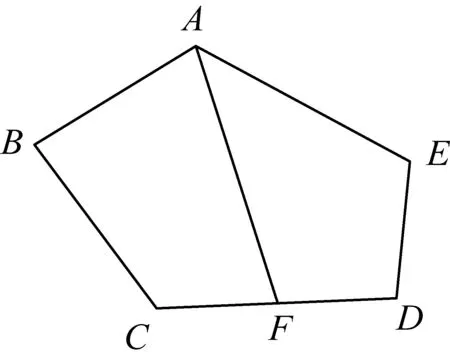
图1

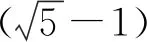
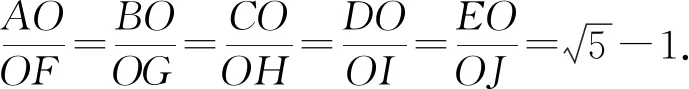
为证明定理，先给出几个引理.

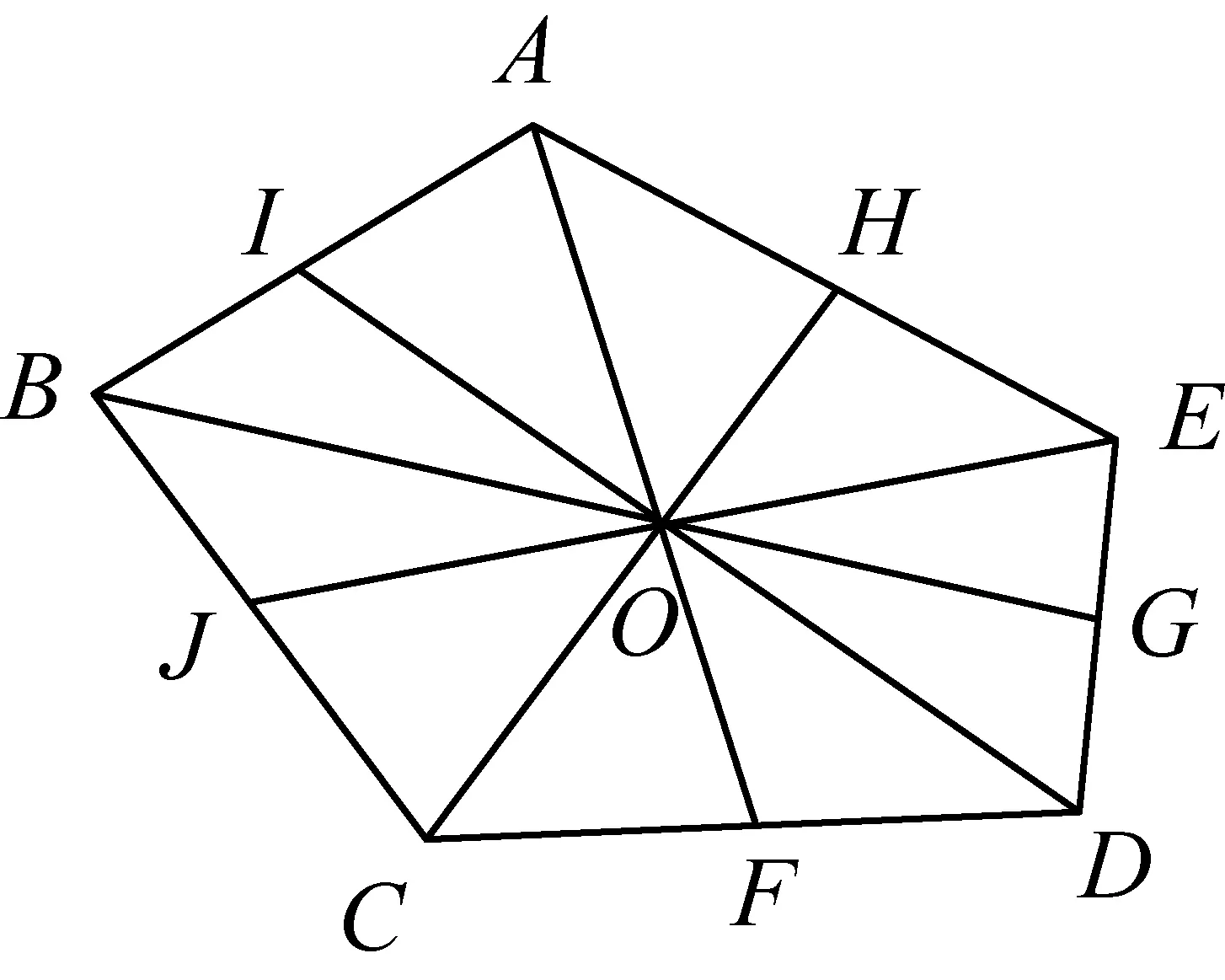
图2

引理1如图3，在△ABC中，E，F是边AC，AB所在直线上的点，BE与CF相较于点P，直线AP交边BC于D，若EF∥BC，则点D是边BC的中点；反之若点D是边BC的中点，P是直线AD上一点，BP，CP分别交直线AC，AB于点E，F，则EF∥BC.

本引理系熟知性质，利用塞瓦定理即得.

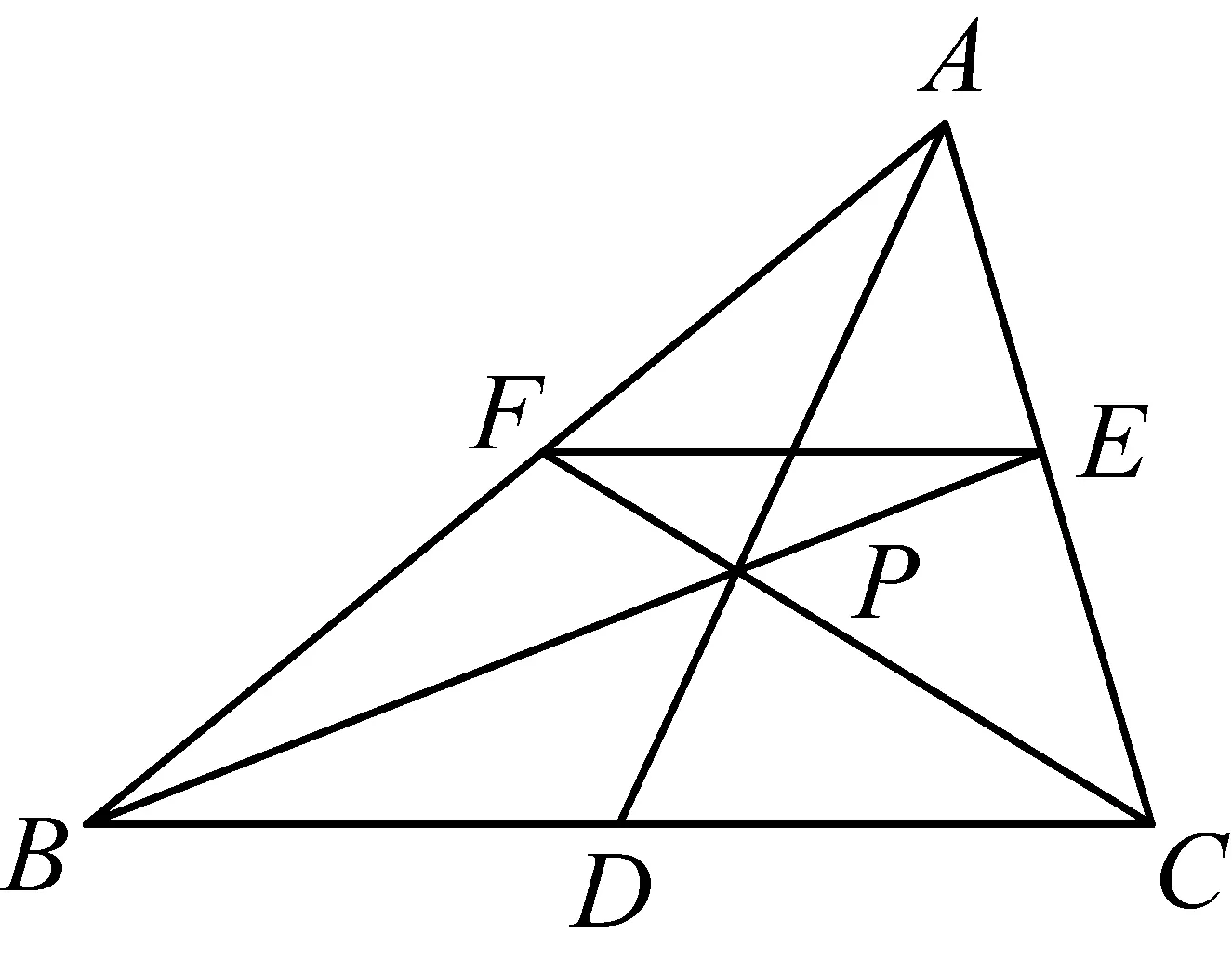
图3

引理2如图4，若五边形ABCDE是规范五边形，则BE∥CD，AC∥DE，BD∥EA，CE∥AB，AD∥BC.

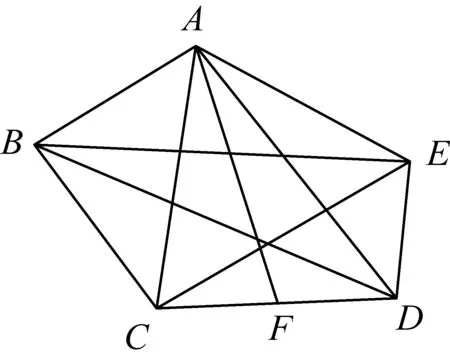
图4

证明设AF是五边形ABCDE的规范中线，

由于S△ACF=S△ADF，则S△ABC=S△ADE，

同理S△ABC=S△CDE，故S△ADE=S△CDE，

所以AC∥DE，其余同理可得.

可得S△ABC=S△BCD=S△CDE=S△DEA=S△EAB.

引理3如图5，五边形ABCDE是规范五边形，AF是它的规范中线，BD，CE交于点M，则A，M，F三点共线.

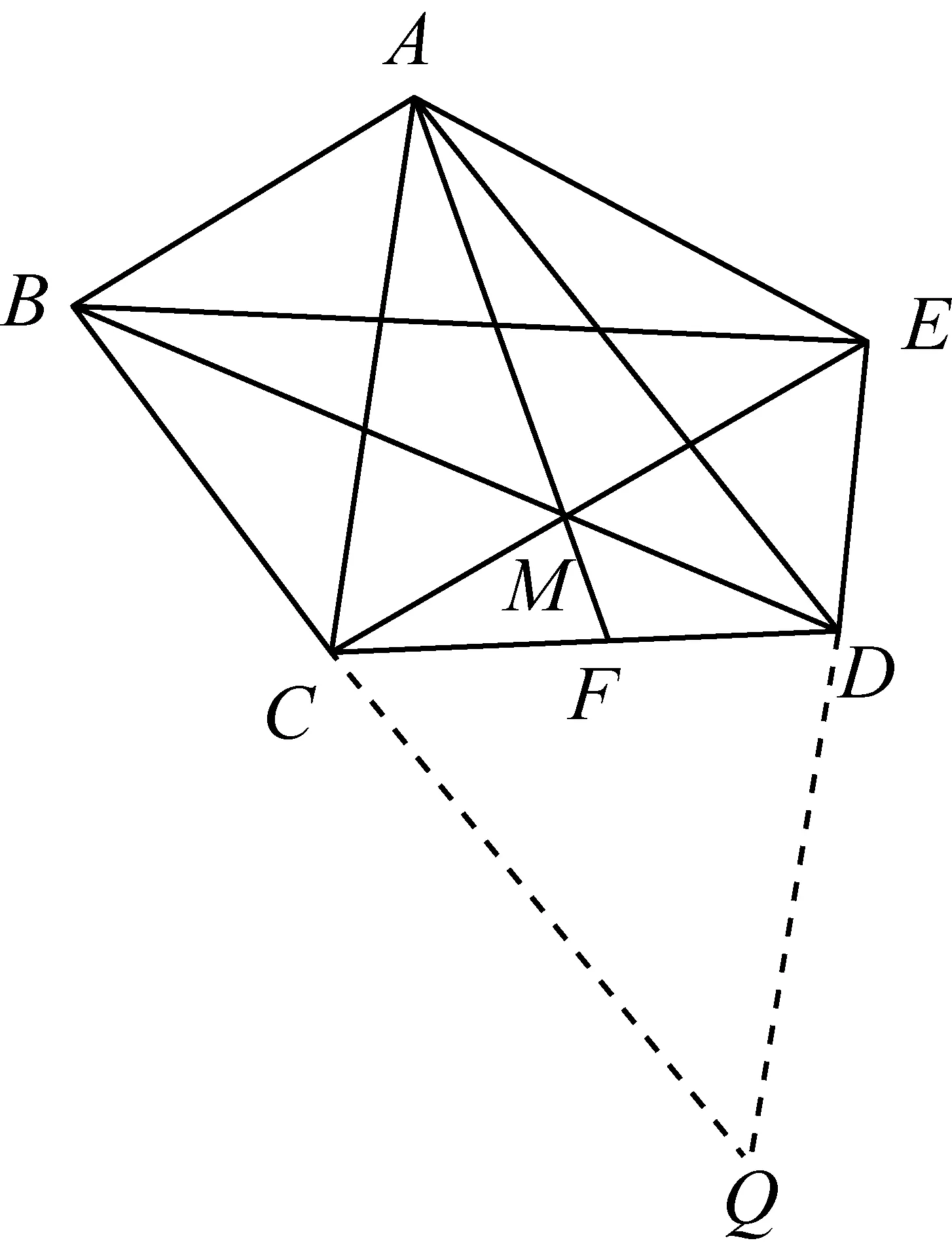
图5

证明延长BC，ED交于点Q，由引理2知四边形ACQD是平行四边形，因为F是CD中点，所以A，F，Q共线，又因为BE∥CD，则由引理1得M，F，Q共线，所以A，M，F三点共线.

定理的证明设规范五边形ABCDE各条对角线的交点如图6所示.由引理3知，只须证AM，BN，CR，DK，EL交于一点即可.

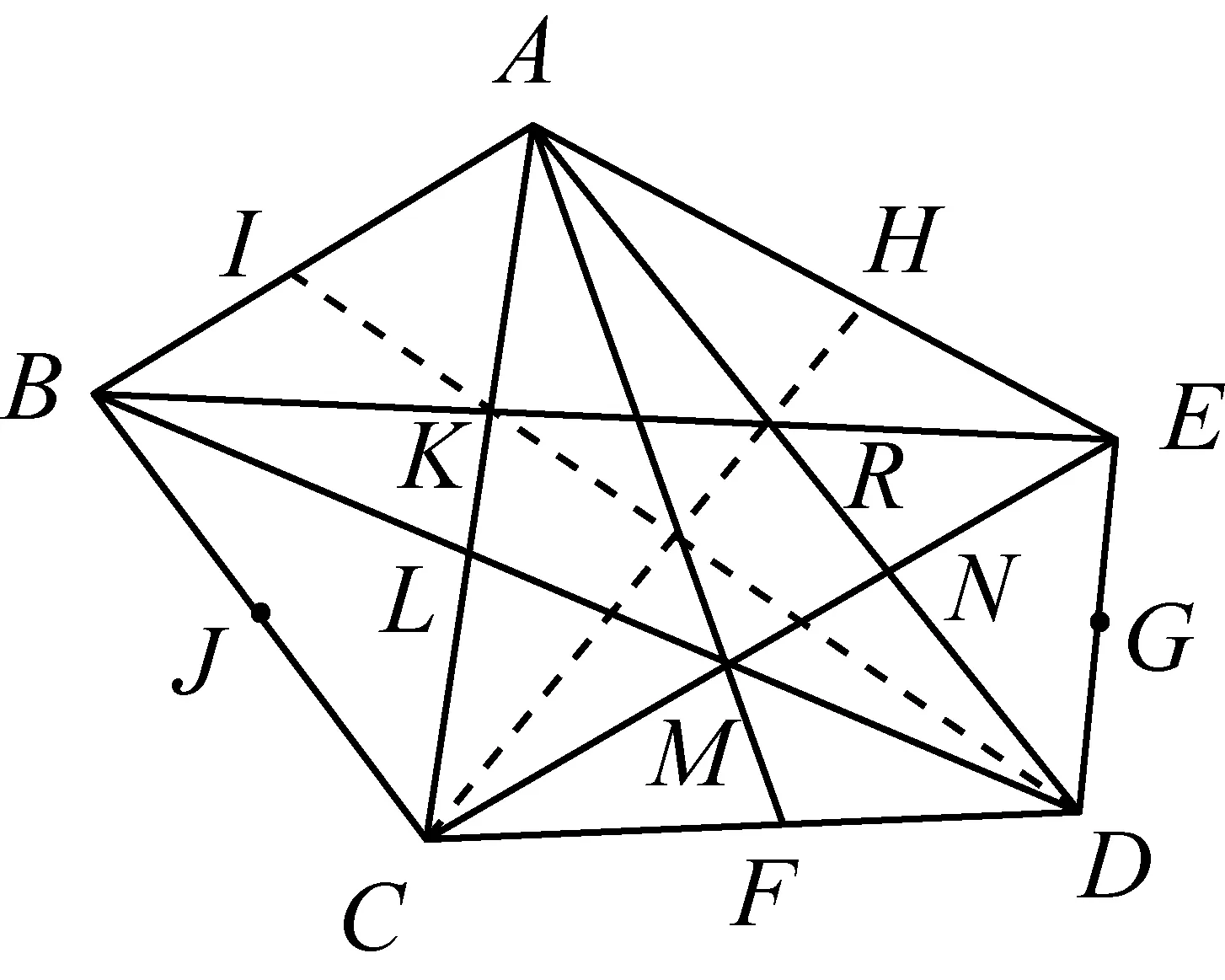
图6

先由引理2得BE∥CD，即KR∥CD，再由引理1知CR，DK的交点必在中线AF上，于是AM，CR，DK交于一点，同理BN，DK，EL交于一点，CR，EL，AM交于一点，DK，AM，BN交于一点，EL，BN，CR交于一点，所以AM，BN，CR，DK，EL交于一点.

接下来证明数量关系：

如图7，延长BC，ED交于点Q，

则四边形ACQD是平行四边形，

根据三角形中位线定理得HI∥BE，

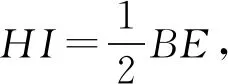
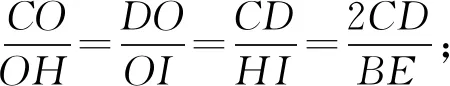
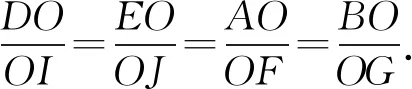
设五边形ABCDE的面积为S，

S△ABC=S△ADE=S△ABE=x，

则S△ACD=S-2x，

由于四边形ACQD是平行四边形，

所以S△DCQ=S△ACQ=S△ACD=S-2x，

易知△CDQ∽△BEQ，故

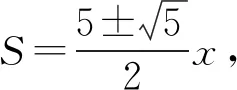
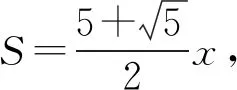
所以

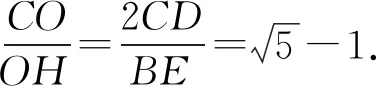
图7

由定理及引理即得如下几个推论.

推论1如图8，若五边形ABCDE是规范五边形，则

上述证明过程中已证.恰好是黄金分割比.

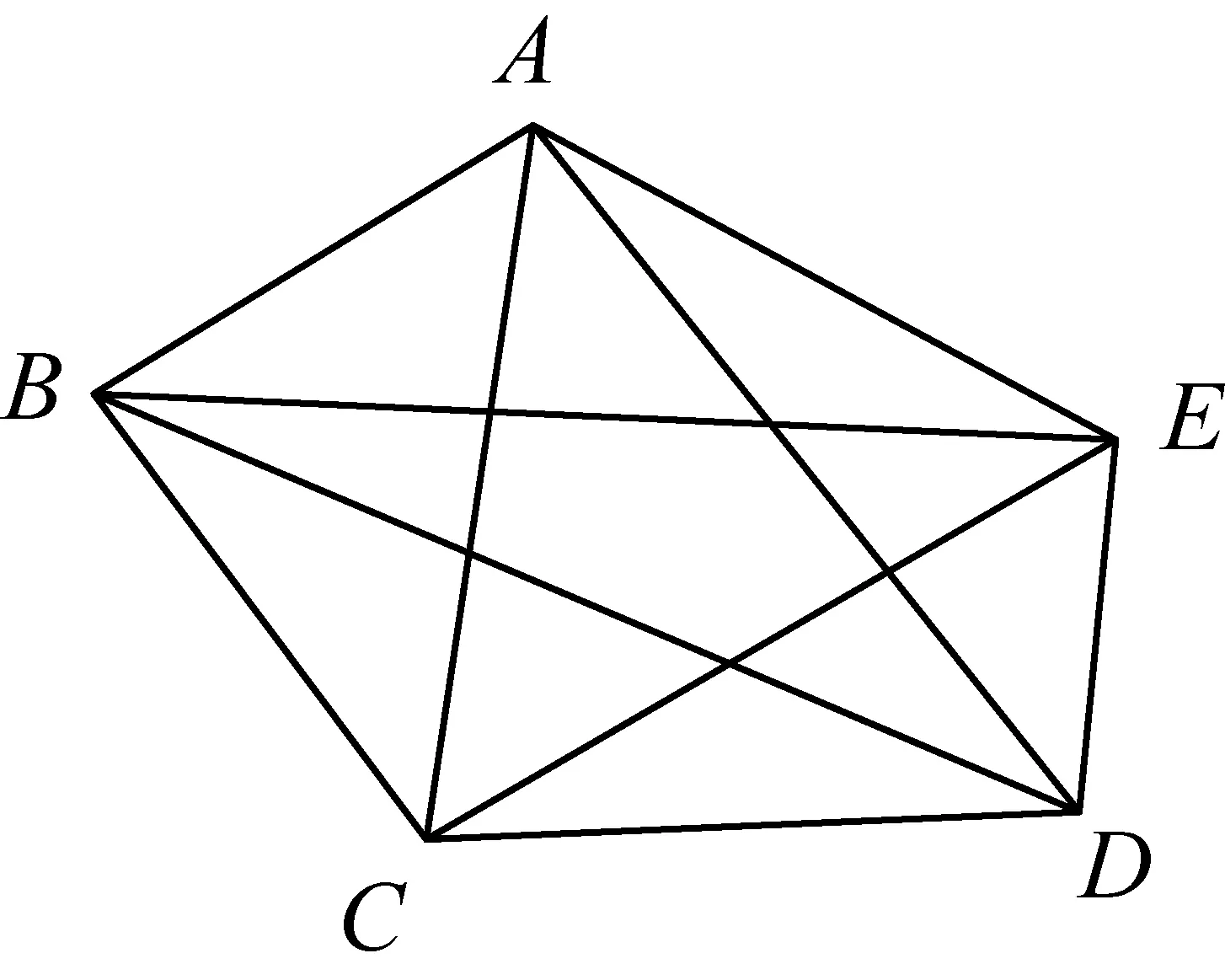
图8

推论2如图8，若五边形ABCDE是规范五边形，面积为S，则

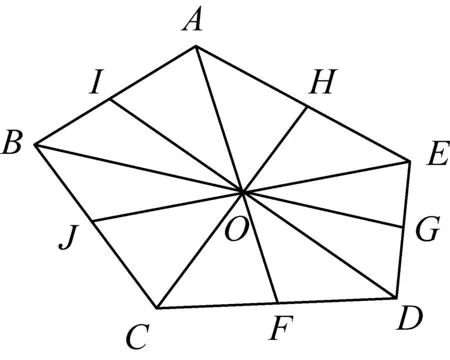
图9

推论3如图9，若五边形ABCDE是规范五边形，则它的五条规范中线AF，BG，CH，DI，EJ连同重心O把五边形分割成10个面积相等的三角形.(即图中所示的小三角形的面积均相等)

推论4如图6，若五边形ABCDE是规范五边形，则它的对角线所交成的五边形KLMNR也是规范五边形，且有公共重心.

利用定理证明过程即可推得.

猜想