三角函数题“正确解法”后的反思

●武瑞雪 (城北中学 江苏睢宁 221200)

“数学题的解后反思”是指在解决了数学问题之后，不是解完了事，而是对题目条件的再思考、再分析，从中发现不足甚至错误，或归纳解题规律.数学家波利亚曾说过：“没有任何一道题是可以解决得十全十美的，总剩下些工作要做，经过充分地探讨，总会有点滴发现，总能改进这个解答，而且在任何情况下，我们总能提高自己对这个解答的理解水平”.这里所说的剩下些工作，就是解题后的反思.本文以三角函数题为例，从以下几个方面阐述如何进行解题后的反思.

1 反思解法好差

解完一道题目后，通过反思解法，可加深对题目条件的本质的领悟.这有利于培养思维的深刻性，提高解题能力和解题速度.

例1 已知点 A(cos80°，sin80°)，B(cos20°，sin20°)，求点 A，B 间的距离.

解由两点间的距离公式得{ θ(θ为参数)，知点 A，B都在单位圆上，且∠AOB=80°-20°=60°，结合圆O的图形易得AB=1.答题时间不足1分(图形不画，只需想像).

其原因是学生在平时练习时，过于机械，没有对解法进行认真选择，出现了思维定势.

2 反思解法规律

解题后，反思解法中有无规律可循，可从特殊题目的解法引申出一般题目的解法.

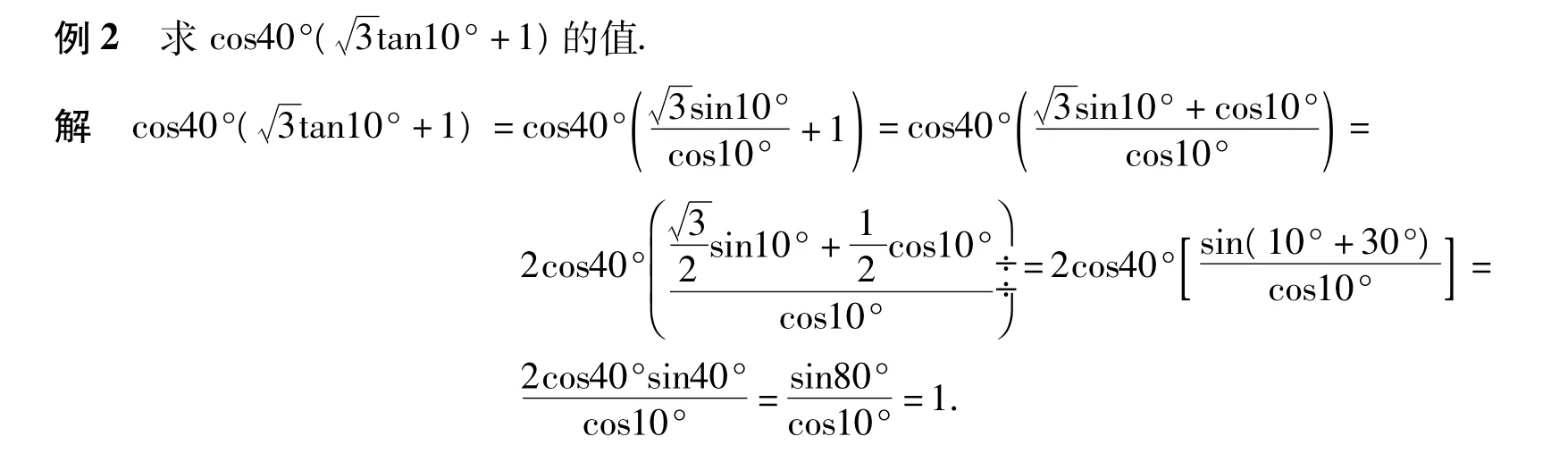
反思 (1)题目中既有正弦，又有正切，常用方法是“切”化“弦”;

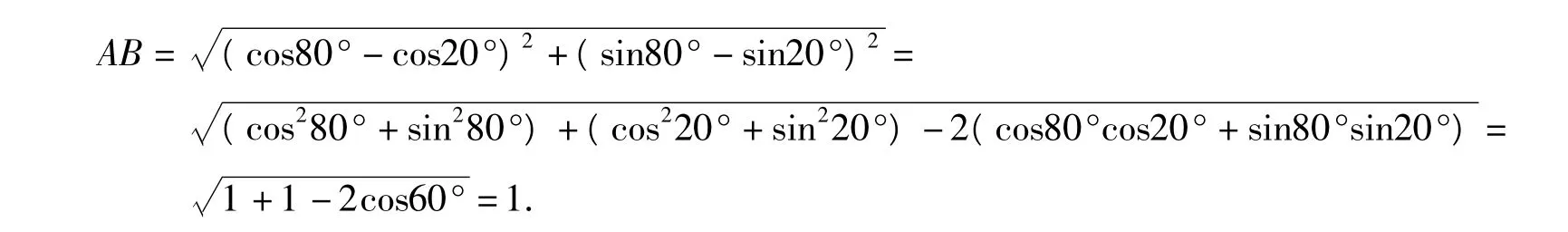
3 反思有无多解(一题多解)

很多题目有多种解法.解完一道题目后，应反思其是否还有另解，以求最简捷的解法，使思维向更高层次发展，培养思维的发散性和灵活性.

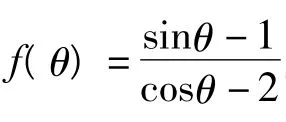
其中φ为辅助角.于是

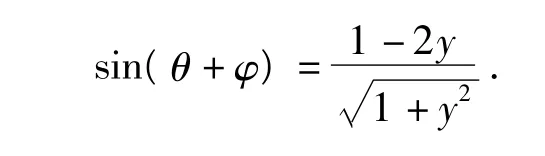
又由|sin(θ+φ)|≤1，得

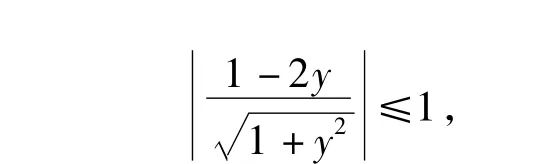
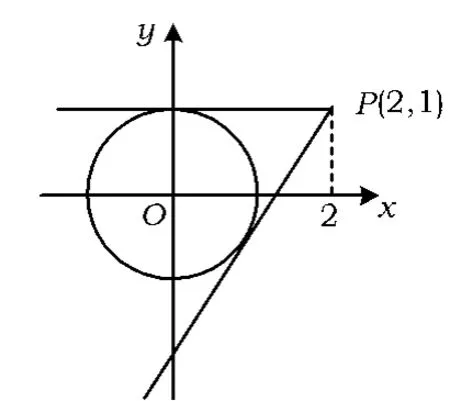
图1

4 反思同类题目

解题后，反思与该题同类的习题(即变式题)，进行对比，找出解答此类题目的技巧和方法，从而达到举一反三、触类旁通的目的.

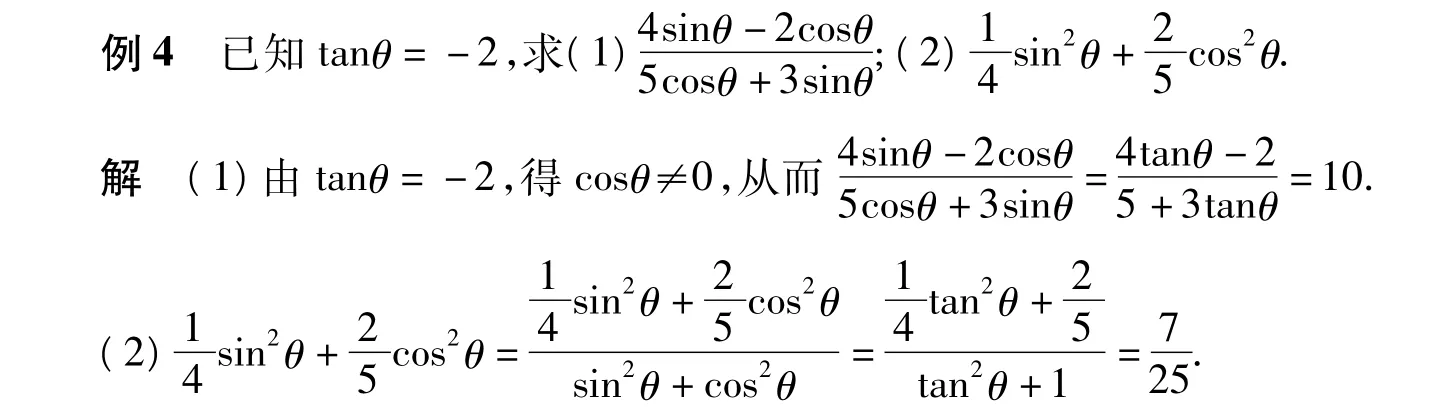
反思 已知tanθ的值，解关于sinθ，cosθ的齐次式化简、求值问题，常常可转化为关于tanθ的函数式求解.虽然已知式或所求式的表达式不同，但其实质相同，通过这样的反思训练，解决此类问题的能力可得到极大提高.

此题得以解决.

5 反思题目结论

当解决一个问题后，常常会出现几种情况或结论，这对解题者而言，不是解题过程的终结，相反，它为解题者提供了一个进行反思的空间：这些情形或结论中有没有多余的解?

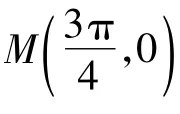
分析 由函数f(x)是R上的偶函数，得f(-x)=f(x)，即

反思 对ω的无数个值，必须反思其存在的合理性.事实上，

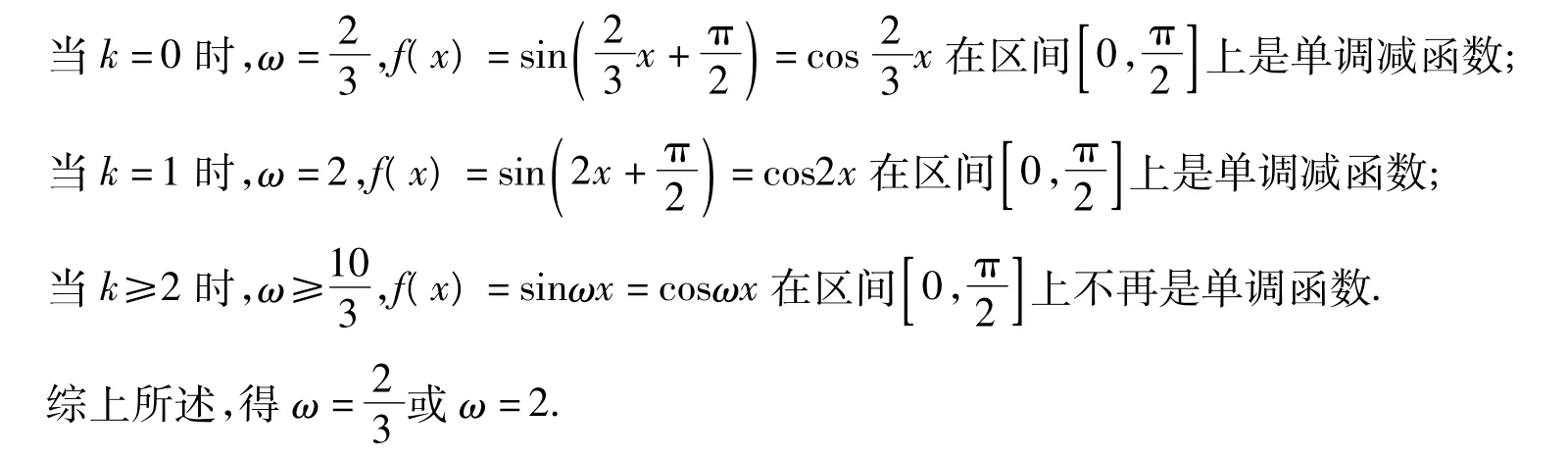
这样，学生在反思的基础上，思维不断得到发展.

6 反思条件与结论的联系

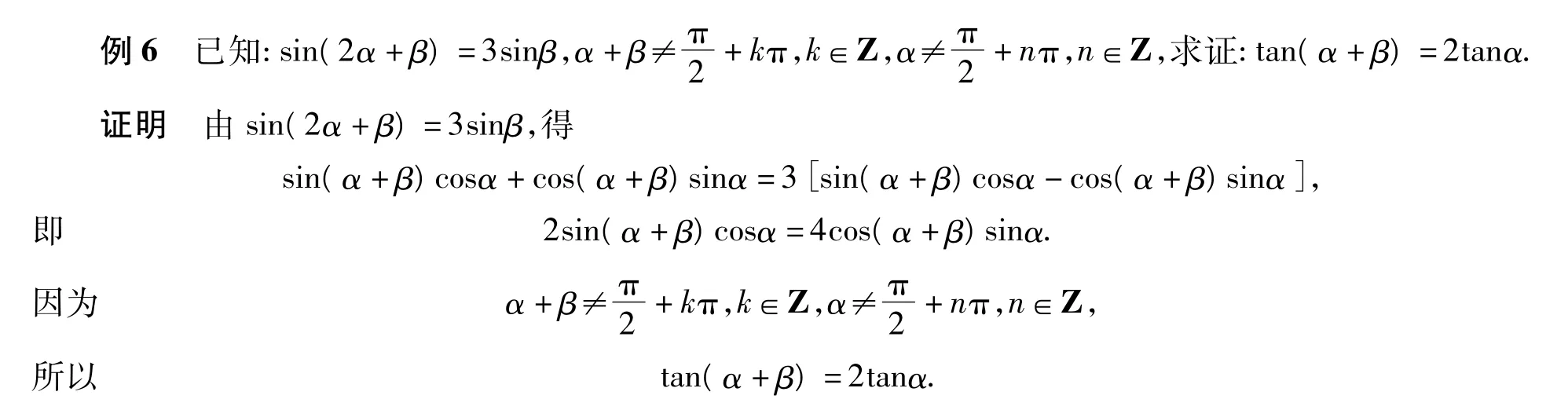
反思 部分学生看到题目后无从下手.仔细分析该题，已知条件等式中的2个角为2α+β与β，所要求证的等式中的2个角为α+β与α.故应设法将已知等式中的2个角2α+β，β向所要求证的等式中的2个角 α+β，α转化(即设法将已知与未知挂上钩)：2α+β=(α+β)+α，β=(α+β)-α，然后以 α+β与 α为基本角，用两角和与差的正弦公式展开，再向正切转化即可证得.

总之，在数学解题后，经常进行以上的反思，有利于学生加深对基础知识和方法的掌握;有利于培养学生思维的深刻性、批判性、创造性、周密性和严谨性;有利于提高学生发现问题、分析问题和解决问题的能力;有利于培养学生的创新意识和科学的思维品质.学生应将反思作为一种习惯.不断地反思，才会不断地进步，才能提高学习效率.