简述非线性递归数列化归的常用策略

●沈宝伟 (诸暨中学 浙江诸暨 311800)

求递推数列的通项是数学竞赛和高考数列题最为常见的考查内容之一，通常可以将它化归为线性递归数列求解.本文就一些典型的非线性递归数列问题的化归进行剖析，介绍几种常用的策略，以期抛砖引玉.

1 因式分解

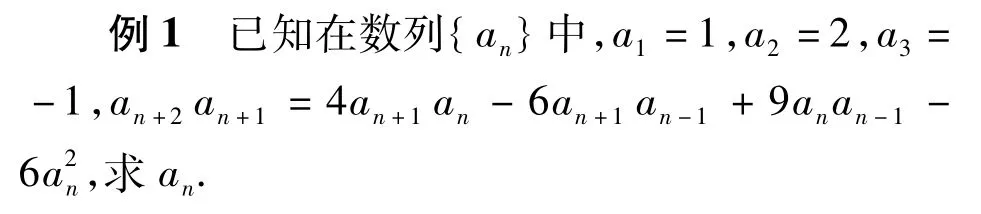
分析该递归数列是非线性齐次递归数列，不能直接用特征根方法.注意到递归式是齐二次式，考虑通过因式分解将其化为一次齐次式.

解因为

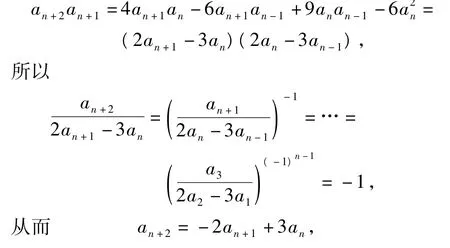
其特征根方程为x2+2x-3=0，解得

2 配方法

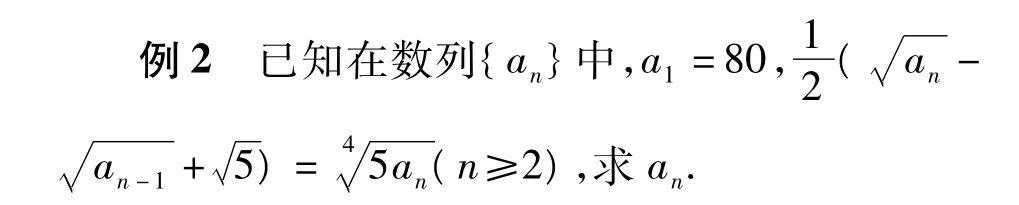
分析该递归数列是非线性递归数列，注意到等式2边根式的次数关系，可考虑用配方法求解.

解配方得

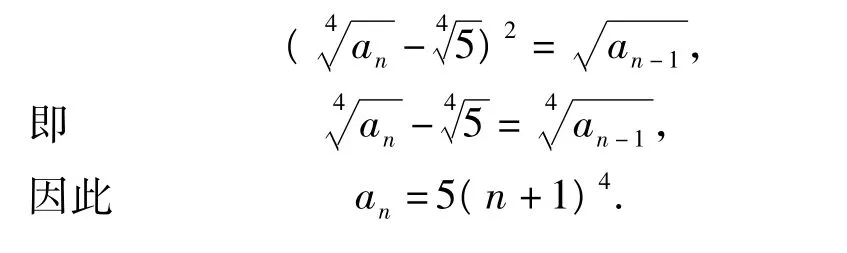
3 待定系数法

(1993年全国高中数学联赛试题)

解将原式变形为

“好”的统计与概率的案例能促进理论和实践的结合，同时案例的开发和收集能为教师提供教学参考和借鉴.从现有文献看，教学案例有31篇，都以现实情境为背景，并设计统计实践活动，但是重复性研究较多.其中，有5篇运用信息技术教学的案例，动态地展现了数据处理过程，但是模拟实验较少.可见，统计与概率案例的有效性在实践中得到充分体现需要一个漫长的积累和检验过程.

说明 形如“an+k=A1an+k-1+A2an+k-2+…+Akan+p(Ai，p都是常数)”的递归数列常常采用待定系数法，构造形如“{an+u}”的齐次线性递归数列求解.

例4 已知在数列{an}中，a1=a2=1，an+2=3an+1+18an+2n，求 an.

分析该递归数列是非线性递归数列，注意到等式右边是含有关于n的指数函数，考虑在等式的2边待定关于n的指数函数，将其化归为线性递归形式.

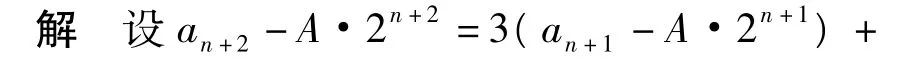
说明 形如“an+k=A1an+k-1+A2an+k-2+…+Akan+mn(Ai，m都是常数)”的递归数列常常采用待定系数法，构造形如“{an+umn}”的齐次线性递归数列求解.

4 换元法

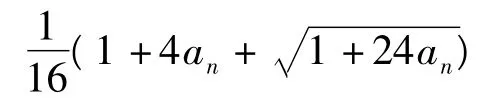
分析该递归数列是非线性递归数列，注意到等式右边含有根号，不方便处理，想到可利用变量换元.

5 取对数法

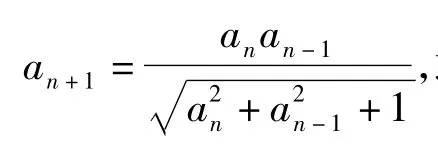
分析该递归数列是非线性的分式型且分母比分子复杂，可先平方取倒数，再因式分解、换元，然后取对数化归为齐次线性递归数列.

解原式平方后取倒数得

6 递推作差

分析该递归数列是非齐次非线性的数列，考虑将其转化为齐次线性递归数列.首先要消去常数，可递推作差消去常数使其化成齐次式，再通过换元使其线性化.

例8 已知数列{an}和{bn}满足a0=1，b0=1，且

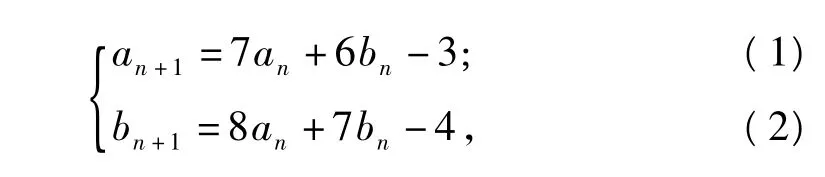
证明：an是完全平方数.

(2000年全国高中数学联赛试题)

分析这是一个二元非齐次线性递归数列，可先将二元降为一元，再递推作差将非齐次线性递归数列化为齐次线性递归数列.

证明由式(1)得

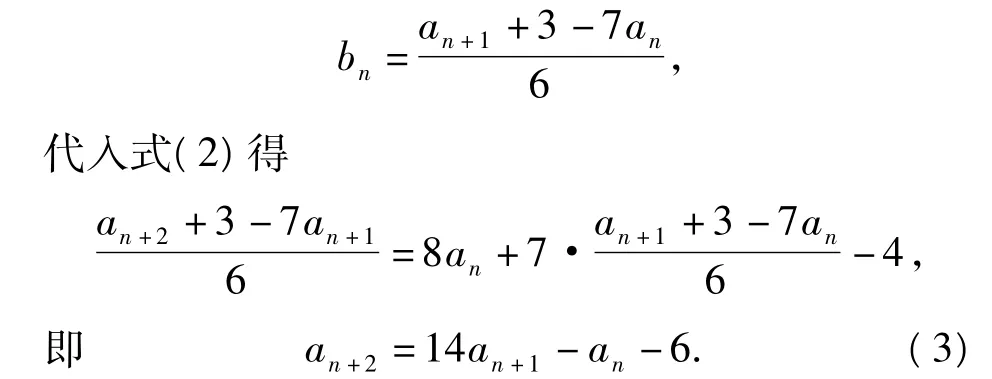
用n+1代换式(3)中的n，得

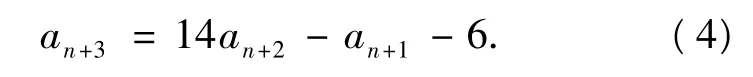
式(4)-式(3)，得

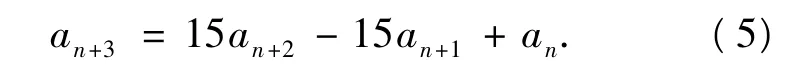
由特征根方程x3-15x2+15x-1=0以及a0=1，a1=4，a2=49，可解得

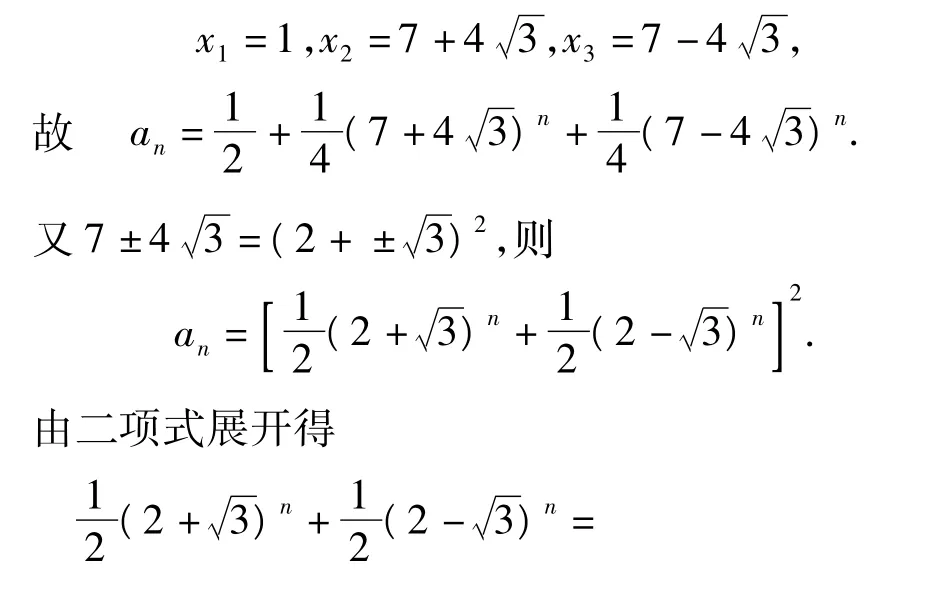
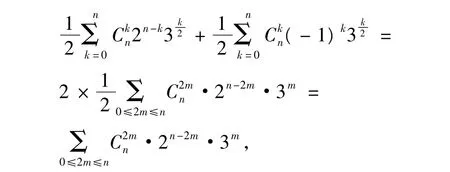
因此an是完全平方数.

说明 形如“an+k=A1an+k-1+A2an+k-2+…+Akan+p(Ai，p都是常数)”的递归数列常常采用递归作差法求解.

7 不动点法

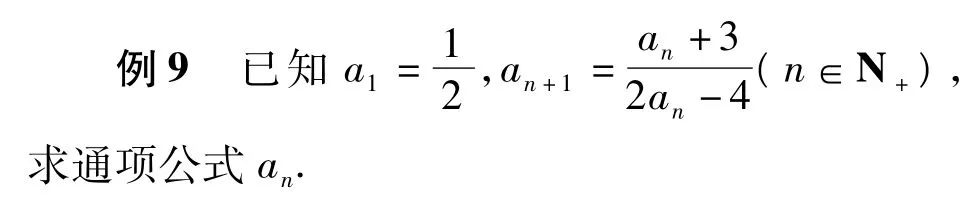
(2005年希望杯数学竞赛培训题)

［1］ 雷波.用不动点法解函数、数列等相关问题［J］.中等数学，2008(10)：12-14.

［2］ 唐立华.长沙一中奥赛标准讲义［M］.北京：龙门书局出版社，2004.