函数y=Asin(ωx+φ)的图像绘制过程教学新解

●张东仓 (电子工业学校 陕西宝鸡 721001)

全日制普通高级中学数学教学大纲(试验修订版)明确指出：按照一定的程序与步骤进行运算、处理数据(包括使用计算器)、简单的推理、画图以及绘制图表等基本技能;良好的个性品质主要是指：正确的学习目的，学习数学的兴趣、信心和毅力，实事求是的科学态度，勇于探索创新的精神，欣赏数学的美学价值.那么，在函数y=Asin(ωx+φ)的图像一节又将如何进一步体现呢?

一般情况下，教师授课会将本节知识能力目标大致确定为：揭示得到函数y=Asin(ωx+φ)(其中A＞0，φ＞0)图像的思维过程.通过参数对函数图像影响的研究及“五点法”画函数图像的介绍，让学生充分体会由简单到复杂、特殊到一般这一化归数学思想.难点确定为：由y=sin(x+φ)的图像得到y=sin(ωx+φ)的图像.

我们把教材中的绘图思路分别称为方案1与方案2，流程图如下所示：

在实际的教学中，尽管笔者使用了几何画板等绘图软件和多媒体技术，但发现本节的教学效果仍不理想.经过认真思考，笔者对教材给出的绘图过程做了一点修改，发现教学效果不错，且该思想可进行推广，适用于由y=f(x)图像得到y=f(kx+b)图像的作图.具体过程如下：

1 新方案绘图步骤

以y=2sin( 2 x +π)为例，即A=2，ω=2，φ=π.2 2第 1步，绘制 y=sin (x +φ)，即 y=ω sin( x +π)的图像(如图1).

4

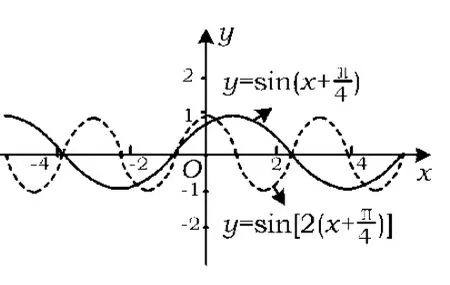
图2

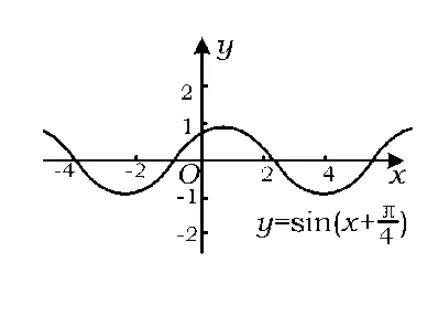
图1

注意：为了形象地演示图2中的虚线怎样得到，可看图3及注释：

图3

图4

2 新、旧方案比较

(1)方案1与方案2在作伸长或缩短变换时，指出将所有点横坐标伸长或缩短.一方面，计算量大;另一方面，手动绘图不可能实现，只是理论上应该如此.新方案更进一步巩固了“五点法”作图.

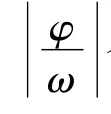
(4)新方案比较容易根据正弦型图像求出表达式 y=Asin(ωx+φ).

基于上面的叙述，有如下结论：

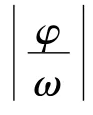
函数y=Asin(ωx+φ)的图像可依据大纲要求：会用“五点法”画正弦函数、余弦函数和函数y=Asin(ωx+φ)的简图.图像的绘制从方法上来讲一般是依据表达式或表格进行描点(如果需要再连结各点)、作图、平移、旋转、对折等以及到本节的对基本初等函数进行拉伸与压缩变化得到y=Asin(ωx+φ)型初等函数的作图法.

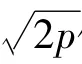
图5

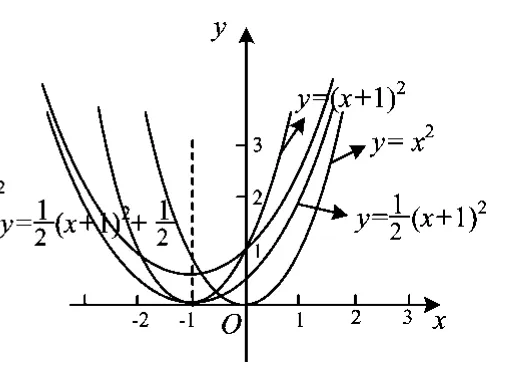
图6

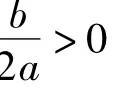
综上所述，有如下结论：

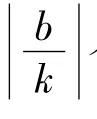
通过对教材中2种方案的改进，一方面可将学生的绘图思想得到解放——从三角函数的绘图推广到由y=f(x)图像得到y=Af(kx+b)图像的作图，从而将他们的绘图技能得到进一步升华.另一方面，培养了学生实事求是的科学态度和勇于探索的精神.