沟通2种“和” 由它来搭桥

●黄元华 (深圳市高级中学 广东深圳 518040)

柯西不等式的一种特殊形式：

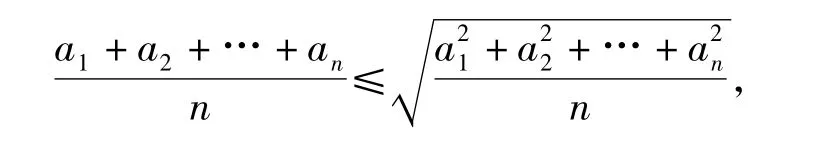
即n个非负数的平方平均值不小于它们的算术平均值.

该不等式的二维形式为：

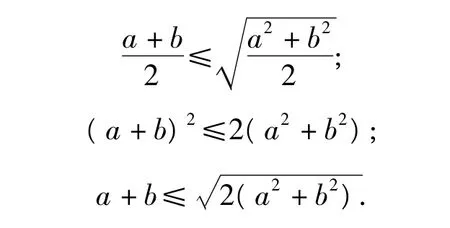
三维形式为：

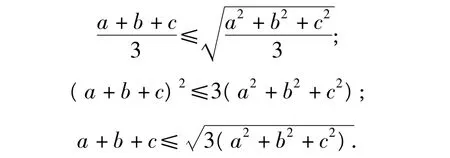
在以上各式中，左边出现了几个非负数的“一次和”，右边出现了这几个非负数的“二次和”，因此这些不等式沟通了几个非负数的“一次和”与“二次和”的联系.当“二次和”为定值时，“一次和”有最大值;当“一次和”为定值时，“二次和”有最小值.

笔者在教学时，用“一次和”、“二次和”这样通俗简练的叙述方式，学生感到新鲜有趣，易于接受，从而激活了课堂，激发了学生的参与热情.

当题目中出现了“一次和”或“二次和”时，就可以考虑用这些不等式来打通关节，探求思路，寻求解题途径.下面举例说明之.

因为二次和为定值，所以一次和有最大值.

评注 此法中把常数1替换为a+b+c，从而使解题过程顺畅、明快.

(2005年全国高中数学联赛第一试试题)

分析要求字母z的范围，需得出关于z的不等式.因而先想到移项，再利用“一次和”与“二次和”的关系产生不等式.

证明将已知等式分别移项得

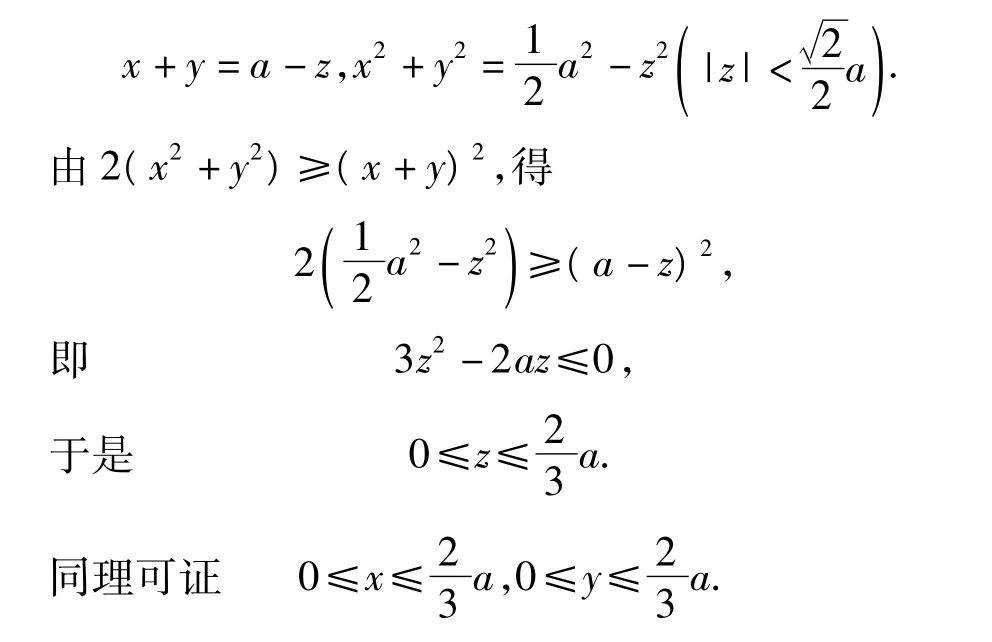
评注此法简便易行，令人赏心悦目.

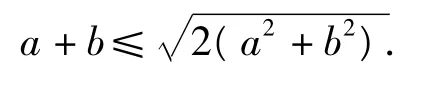
评注此法简捷、明快.一般资料书上提供的证法都要用到较复杂的配凑技巧.

综上所述，巧妙借助“一次和”与“二次和”的关系，的确能解决很多有关不等式证明、求最值等方面的问题.在具体的解题实践中，题目中不一定出现“一次和”或“二次和”，这就需要我们灵活变通，或等价转化，或巧妙构造.