应用题的类型和求解策略

●王元真 (德清县第一中学 浙江湖州 313200)

1 走进应用世界

1.1 常见的一些应用问题

(1)优化问题：实际生活中的“优选”、“控制”等问题常需建立“不等式模型”和“线性规划”问题解决.

(2)预测问题：经济计划、市场预测这类问题通常设计成“数列模型”来解决.

(3)最(极)值问题：工农业生产、建设及实际生活中的极限问题常设计成“函数模型”，从而转化为求函数的最值.

(4)等量关系问题：建立“方程模型”解决.

(5)测量问题：可设计成“图形模型”利用几何知识解决.

1.2 求解应用题的一般思路

可表示如下：

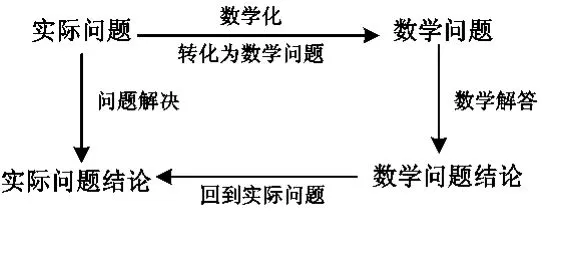
1.3 求解应用题的一般程序

(1)读：阅读理解文字表达的题意，分清条件和结论，理顺数量关系，这一关是基础.

(2)建：将文字语言转化为数学语言，利用数学知识，建立相应的数学模型熟悉基本数学模型，正确进行建模，是关键的一关.

(3)解：求解数学模型，得到数学结论，要充分注意数学模型中元素的实际意义，更要注意巧思妙作，优化过程.

(4)答：将数学结论还原为实际问题的结果.

1.4 解决应用题需过的三关

(1)阅读理解关：一般数学应用题的文字阅读量都比较大，要通过阅读审题，找出关键词、句，理解其意义.

(2)建模转化关：即建立实际问题的数学模型，将其转化为数学问题.

(3)数理求解关：运用恰当的数学方法去解决已建立的数学模型.

2 常见应用模型

题型1 函数模型

例1 某厂生产某种零件，每个零件的成本为40元，出厂单价定为60元.该厂为鼓励销售商订购，决定当一次订购量超过100个时，每多订购一个，订购的全部零件的出厂单价就降低0.02元，但实际出厂单价不能低于51元.

(1)当一次订购量为多少个时，零件的实际出厂单价恰降为51元?

(2)设一次订购量为x个，零件的实际出厂单价为P元，写出函数P=f(x)的表达式;

(3)当销售商一次订购500个零件时，该厂获得的利润是多少元?如果订购1 000个，利润又是多少元(工厂售出一个零件的利润=实际出厂单价-成本)?

考点分析 本题主要考查函数的基本知识和分段函数的概念，考查应用数学知识分析问题和解决问题的能力.

解题思路 (1)设每个零件的实际出厂价恰好降为51元时，一次订购量为x0个，则

因此当一次订购量为550个时，每个零件的实际出厂价恰好降为51元.

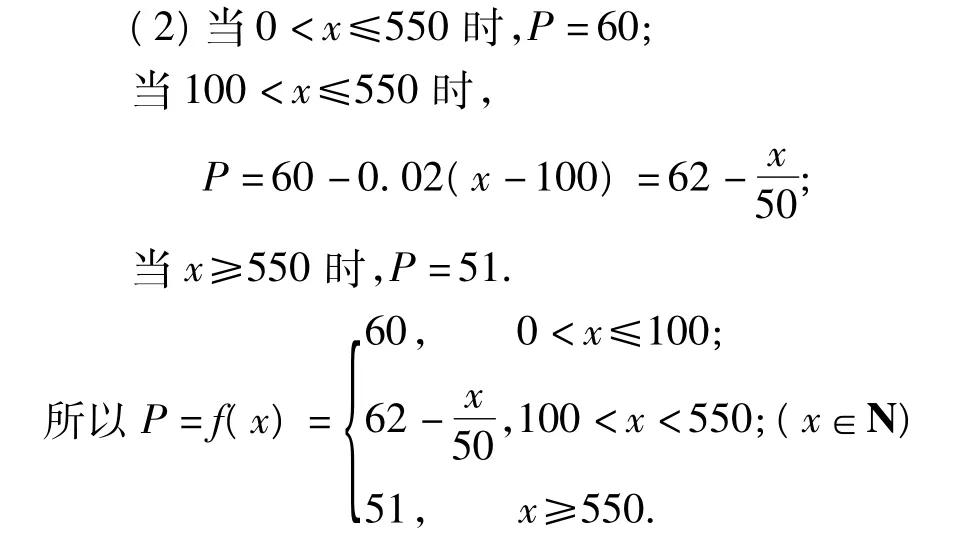
(3)设销售商的一次订购量为x个时，工厂获得的利润为L元，则

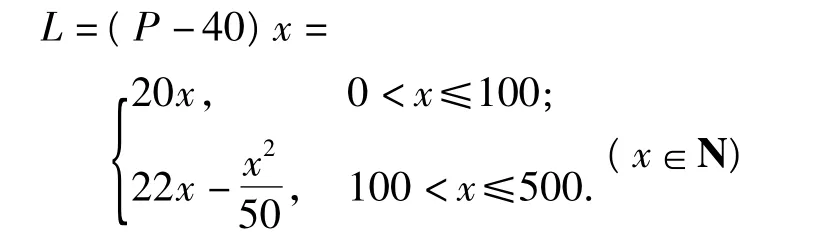
当x=500时，L=6 000;当 x=1 000时，L=11 000.

因此，当销售商一次订购500个零件时，该厂获得的利润是6 000元;若订购1 000个，则利润是11 000元.

点评与拓展 根据题意，熟练地建立函数模型，运用函数性质、不等式等知识处理所得的函数模型.

题型2 不等式模型

例2 已知甲、乙、丙3种食物的维生素A，B的含量及成本如表1.若用甲、乙、丙3种食物各x kg，y kg，z kg配成100 kg混合食物，并使混合食物内至少含有56 000单位维生素A和63 000单位维生素B.

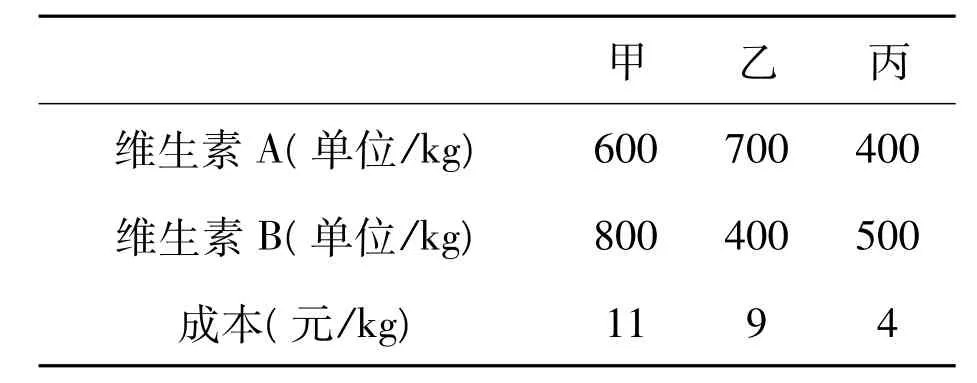
表1 食物的维生素A，B含量及成本

(1)用x，y表示混合食物成本c元;

(2)确定 x，y，z的值，使成本最低.

考点分析 本题考查的知识点是不等式和线性规划问题，考查应用数学知识分析问题和解决问题的能力.

解题思路 (1)由题意得

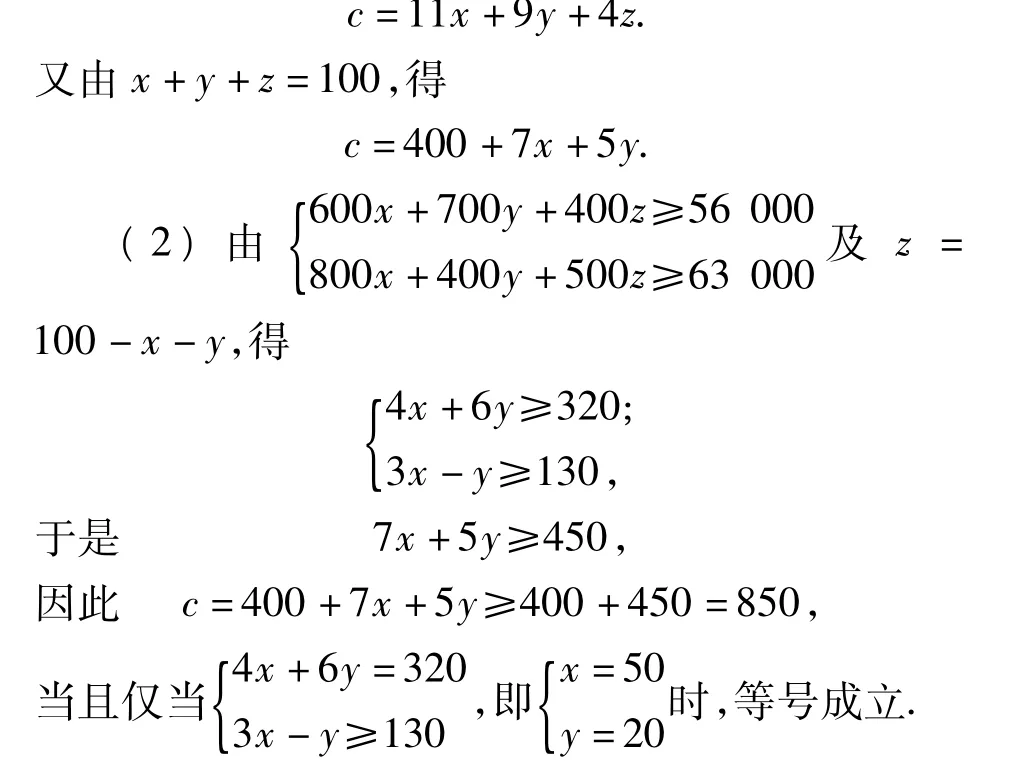
因此当 x=50 kg，y=20 kg，z=30 kg时，混合物成本最低，为850元.

点评与拓展 本题为线性规划问题，用解析几何的观点看，问题的解实际上是由4条直线所围成的区不难发现，应在点M(50，20)处取得.

图1

题型3 几何模型

例3 某工厂生产容积为π立方米的圆柱形无盖容器，制造底面的材料每平方米30元，制造侧面的材料每平方米20元，设计时材料的厚度及损耗可以忽略不计.

(1)把制造容器的成本y(元)表示成容器底面半径为x(米)的函数，并指出当底面半径为多少时，制造容器的成本最低?求出最低成本.

(2)若为某种特殊需要，要求容器的底面半径不小于2(米)，则最低成本为多少元(精确到1元)?

考点分析 本题考查的知识点是立体几何中圆柱的概念，函数和不等式的运用.能力是根据题意，熟练地建立函数模型，运用函数性质、不等式等知识来处理所得的最值问题.

解题思路 (1)设圆柱形容器的高为h，则

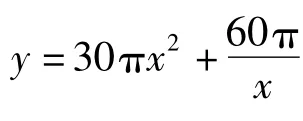
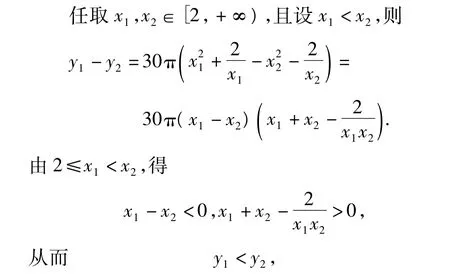
于是函数y=30πx2+60π x在区间［2，+∞)上单调递增.故当x=2时，y取得最小值为：150π≈471(元).

点评与拓展 均值不等式求解时要注意等号成立的条件.

题型4 数列模型

例4 某商场经过市场调查分析后得知，2003年从年初开始的前n个月内，对某种商品需求的累计数f(n)(万件)近似地满足下列关系：

(1)问这一年内，哪几个月需求量超过1.3万件?

(2)若在全年销售中，将该产品都在每月初等量投放市场，为了保证该商品全年不脱销，每月初至少要投放多少件商品(精确到件)?

考点分析 本题考查的知识点是数列和不等式的应用，能力是培养学生应用数学知识分析问题和解决问题的能力.

解题思路 (1)首先，第n月的月需求量满足

本文所采用数据主要来自于2015年全国1%人口抽样调查汇总数据。此次调查是以2015年11月1日零时为标准时点，以全国为总体，以各地级市(地区、盟、州)为子总体，采取分层、二阶段、概率比例、整群抽样的方法，对我国境内抽中调查小区内的全部人口(不包括港澳台居民和外国人)进行调查，最终样本量为2131万人，占全国总人口的1.55%，其中样本中农民工总量为935.6万人，河北省农民工总量为56.8万人。具体数据如表1。

即这一年的5，6月的需求量超过1.3万件.

(2)设每月初等量投放商品a万件，要使商品不脱销，对于第n月来说，不仅有本月投放市场的a万件商品，还有前几个月未销售完的商品.因此只需na-f(n)≥0，即

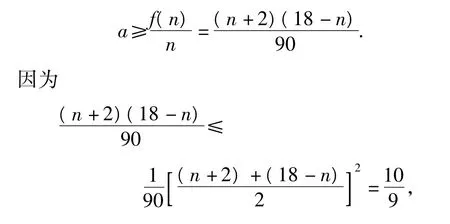
点评与拓展 实际问题的解答要注意其实际意义.本题中的最小值不能用四舍五入的方法得到，否则不符合题意.

题型5 概率模型

例5 A，B两个代表队进行乒乓球对抗赛，每队3 名队员，A 队队员是 A1，A2，A3，B 队队员是 B1，B2，B3.按以往多次比赛的统计，对阵队员之间胜负概率如表2.

表2 对阵队员之间胜负概率

现按表中对阵方式出场，每场胜队得1分，负队得0分，设A队、B队最后所得总分分别为ξ，η.

(1)求ξ，η的概率分布;

考点分析 本小题考查离散型随机变量分布列和数学期望等概念，考查运用概率知识解决实际问题的能力.

解题思路 (1)ξ，η的可能取值分别为3，2，1，0，于是

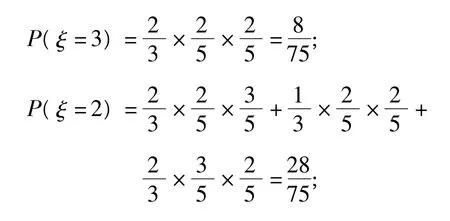
点评与拓展 高考应用性问题的热门话题是增减比率型和方案优化型，另外估测计算型和信息迁移型也时有出现.求解应用题的一般步骤是(四步法)：

(1)读题：读懂和深刻理解，译为数学语言，找出主要关系;

(2)建模：把主要关系近似化、形式化，抽象成数学问题;

(3)求解：化归为常规问题，选择合适的数学方法求解;

(4)评价：对结果进行验证或评估，对错误加以调节，最后将结果应用于现实，作出解释或验证.

题型6 三角模型

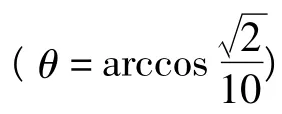
考点分析 考查学生的空间想象能力和运用所学知识解决实际问题的能力.

图2

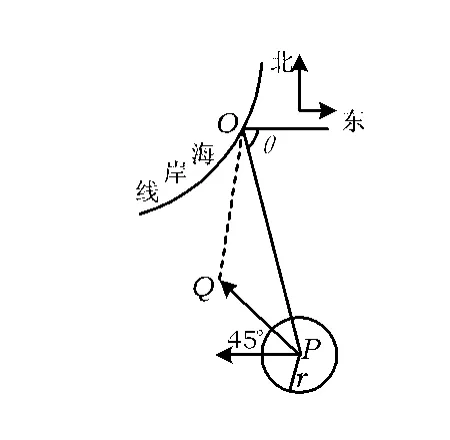
图3

解法1 设在时刻t(h)台风中心为Q(如图3)，此时台风侵袭的圆形区域半径为10t+60(km).若在时刻t城市O受到台风的侵袭，则

即12小时后该城市开始受到台风的袭击.

解法2 以点P为原点，正东方向为x轴的正方向，建立直角坐标系(如图4).

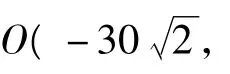
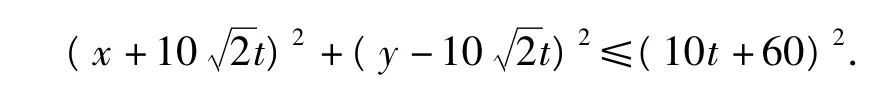
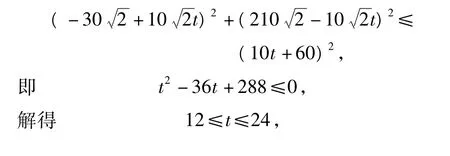
点评与拓展 以预测台风影响时间为背景，通过对题中给出信息的分析，准确地理解台风运动的规律，综合应用有关的知识和方法建立适当的数学模型.

图4

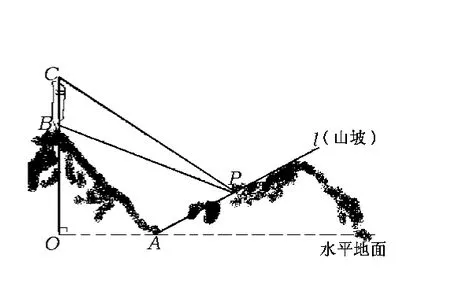
图5

题型7 测量模型

例7 某人在一山坡P处观看对面山项上的一座铁塔，如图5所示，塔高BC=80(米)，塔所在的山高OB=220(米)，OA=200(米)，图中所示的山坡可视为直线l且点P在直线l上，与水平地面的夹角为 α，tanα=，试问此人距水平地面多高时，观看塔的视角∠BPC最大(不计此人的身高).

考点分析 这是一道解析几何与函数综合在一起的应用题，通过计算直线的斜率，一条直线与另一条直线的夹角公式获得函数的表达式.

图6

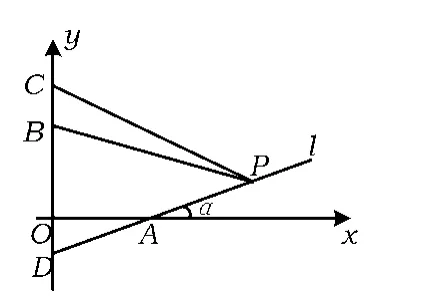
图7

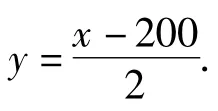
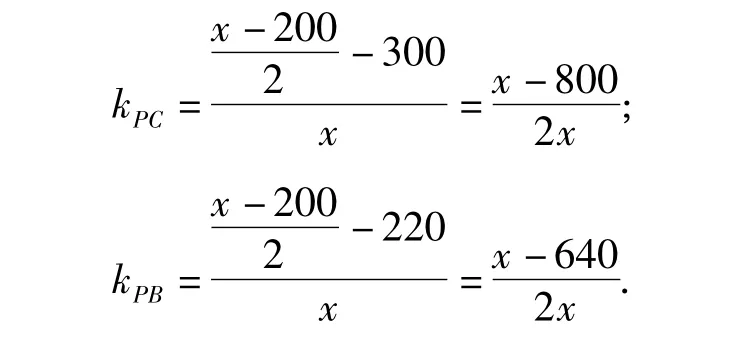
又由直线PC到直线PB的角的公式，得

因此当∠tanBPC最大时，∠BPC为最大.故当此人距水平地面60米高时，观看铁塔的视角∠BPC最大.

题型8 二次曲线模型

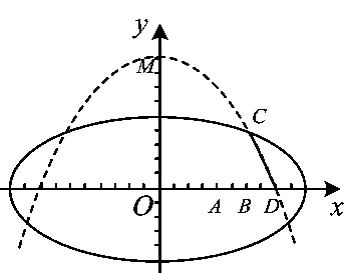
图8

(1)求航天器变轨后的运行轨迹所在的曲线方程;

(2)试问：当航天器在x轴上方时，观测点A，B测得离航天器的距离分别是多少时，应向航天器发出变轨指令.

考点分析 与光学、力学、轨迹等有关的应用问题，可通过建立适当的坐标系，运用曲线的知识建立数学模型解答，且主要研究的是二次曲线，因此可称之为二次曲线模型.

解题思路 (1)设曲线方程为题意可知，降落点D(8，0)在曲线上，则

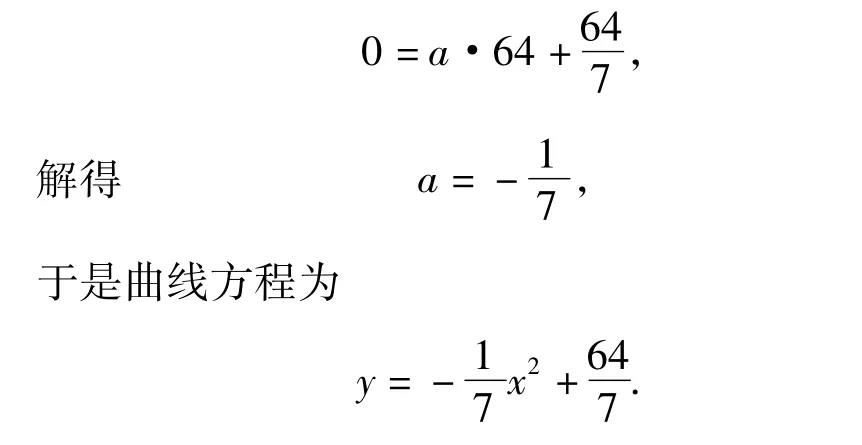
(2)设变轨点为C(x，y).根据题意可知，由

将y=4代入椭圆方程得

x=6或x=-6(不合题意，舍去)，因此点C的坐标为(6，4).于是

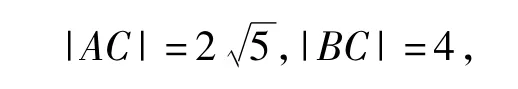
点评与拓展 本题是一道立意新颖、难度适中的数学应用题，题目以大家非常感兴趣的宇宙航行问题为背景，设计了航天器变轨返回试验问题.数学模型是已知的，又是大家熟悉的，问题的提出则是已知抛物线的顶点和另一点的坐标，求抛物线的方程以及求椭圆与抛物线的交点的坐标和两点间的距离等熟悉的内容，但是改成实际问题之后，就能考查应用数学知识解决实际问题能力和分析问题与解决问题的能力.把考知识的题目变成了考能力、考思维的题目.