矩阵方程AXB =C最小二乘D对称解的通解
2010-05-09屈立新
屈立新
矩阵方程=最小二乘对称解的通解
屈立新1,2
(1. 湖南大学 数学与计量经济学院, 湖南 长沙, 410082; 2. 长沙商贸旅游职业技术学院, 湖南 长沙, 410004)
利用矩阵对的标准相关分解, 得到了=最小二乘对称解的表达式, 推广了已有的结果.
矩阵方程; 最小二乘对称; 通解
1 引言及引理
约束矩阵方程问题是指在一定的约束条件下求解矩阵方程的解或者最小二乘解以及相应的最佳逼近解. 该问题在结构设计[1]、参数识别、非线性规划、有限元、生物学、固体力学、以及自动控制理论[2]等方面都有重要的应用.
求解矩阵方程的约束解一般有直接法和迭代法2种方法. 直接法是从矩阵分解理论出发, 利用矩阵的各种分解, 如奇异值分解[3]、QR分解[4]、矩阵对的广义奇异值分解[5]和标准相关分解[6]等, 得出矩阵方程有解的充要条件和相容解以及最小二乘解的通式, 或者利用矩阵拉直方法以及矩阵Kronecker积的性质[7], 将矩阵方程问题转换为线性方程组问题, 从而利用线性方程组的理论求矩阵方程=的最小二乘解. 王世轩、孟纯军等[8]研究了矩阵方程=的对称最小二乘解及相应的最佳逼近解. 本文利用矩阵对的广义奇异值分解, 研究了=无解时, 相应的最小二乘解, 并给出了通解的表达式.
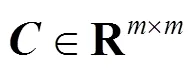


有唯一的对称解其表达式为:

其中*表示矩阵的Hardmand乘积.


所以,

证毕.
2 定理及证明
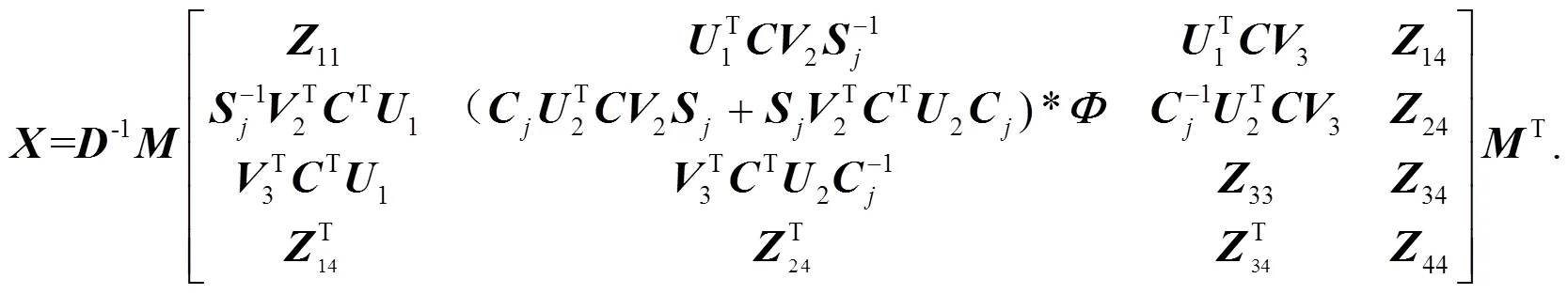
其中, 子块14,24,34为相应阶数的任意块, 而子块11,33,44为相应阶数的任意对称子块.
证明由于

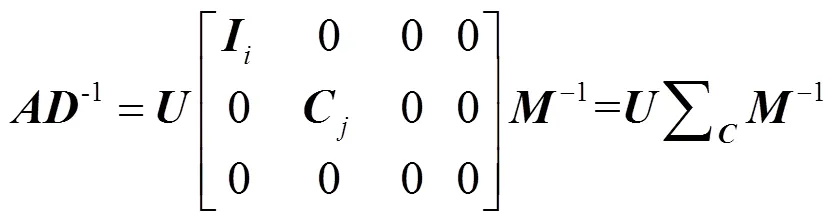




所以, 式(10)就等价于:
,(12)
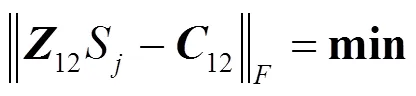

和



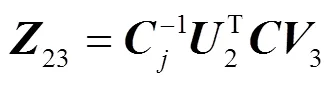

由于

将式(13)、(14)代人式(17), 利用矩阵的对称性, 可得到式(6). 证毕.
[1] 周树荃, 戴华. 代数特征值反问题[M]. 郑州: 河南科学技术出版社, 1991: 1-120.
[2] 须田信英. 自动控制中的矩阵理论[M]. 北京:科学出版社, 1979: 1-150.
[3] 詹兴致. 矩阵论[M]. 北京:高等教育出版社, 2008: 46-66.
[4] 曹志浩. 数值线性代数[M]. 上海:复旦大学出版社, 1995: 1-46.
[5] Gene H Golub, Charles F Van Loan. Matrix Computati- on[M]. 3rd Ed.: The John Hopkins University Press. 1996: 240-513.
[6] Gene H Golub, Zha Hongyuan. Perturbation analysis of the canonical correlations of matrix pairs[J]. Linear Alge- bra and Its Application, 1994, 210: 3-28
[7] 陈公宁. 矩阵理论与应用[M]. 2版. 北京: 科学出版社, 2007: 140-190.
[8] 王世轩, 孟纯军, 胡锡炎.内积空间下对称矩阵最小二乘解及其最佳逼近问题[J]. 模糊系统与数学, 2007, 11(21): 97-100.
The least-squares-symmetric solutions of the matrix equation
QU Li-xin1.,2
(1. College of Mathematics and Econometrics, Hunan Univ, Changsha 410082, China; 2.Changsha Commerce and Tourism College, Changsha 410004, China)
Applying generalized conjugate gradient method, the general expression was obtained for the Least-squares-symmetric solutions of the Matrix equation. The existing results has been extended .
constrained matrix equation; Least-squares- symmetric Solutions;general solution
O 151.21
A
1672-6146(2010)03-0005-02
10.3969/j.issn.1672-6146.2010.03.003
2010-05-08
国家自然科学基金资助项目(10571047)
屈立新(1970-), 男, 硕士,讲师,研究方向为计算算法.
