基于波浪式矩阵置换的稀疏度均衡分块压缩感知算法
2019-01-07杜秀丽
杜秀丽,张 薇,陈 波
(辽宁省通信网络与信息处理重点实验室(大连大学 信息工程学院 ), 辽宁 大连 116622)(*通信作者电子邮箱dxlxts@126.com)
0 引言
压缩感知(Compressed Sensing, CS)[1-3]是一种新兴的信号处理技术,对传统的采样编码技术提出了挑战,是信息领域的一次重要变革。它以观测矩阵为手段,可以以低于奈奎斯特采样定理规定的采样率采样,突破了传统图像采样定理的限制。
分块CS(Block CS, BCS)[4-6]解决了压缩感知中存储资源浪费且重构时间长的难题。长期以来,分块压缩感知技术是图像压缩感知技术中的热点问题,得到了国内外专家和学者的广泛重视。为了消除块效应,各专家学者做了大量的研究[7-11]。
Guicquero等[7]利用图像边缘信息进行自适应压缩感知,算法复杂度较高,且对于复杂图像的重构效果不理想。Li等[8]提出一种基于全变分 (Total Variation, TV)范数的图像分块压缩感知算法,通过全变差分测量稀疏度[9]结构,但全变差分在稀疏度结构的估量上准确度不高。张淑芳等[10]利用离散余弦变换(Discrete Cosine Transform, DCT)后各图像块的DCT系数作为稀疏度判断准则,提出粗糙自适应压缩采样方法,但其采样率及稀疏度阈值的确定具有很强的主观性,不能充分体现自适应压缩采样的优势。王玥等[11]提出了一种基于灰度熵的自适应全变分滤波的压缩感知算法,通过图像的灰度熵自适应分配块采样率提高重构质量,但灰度熵的使用没有考虑图像元素间的相关关系,有一定局限。王蓉芳等[12]提出一种基于视觉显著性的分块自适应压缩感知算法,在采样阶段,每个子块的采样率依据显著信息自适应地变化;在重建阶段,根据不同图像显著信息的差异,自适应地滤波。
图像分块后各子块的稀疏度是不一样的,稀疏度小的子块重构效果差,稀疏度大的子块重构质量好,不同重构效果的子块合成一幅图像时便会出现块效应。而上述研究都是从自适应采样的角度出发,通过为不同稀疏度的子块分配不同的采样率来消除块效应[13]。Zhang等[14]为减小采样率分配不精确带来的误差,同时消除自适应采样中存储多个测量矩阵的缺陷,对图像块本身做处理,提出一种基于矩阵置换的BCS(BCS with Mmatrix Permutation, BCS-MP)算法,通过重新排列所有子块的列向量来改变子块的稀疏度,使各个图像子块的稀疏度均衡,这样可以采用相同的测量矩阵进行采样,同时减小采样的难度和重构时的块效应;但算法中采用顺序的排序方法,使得子块间稀疏度均衡效果较差。
针对上述子块间稀疏度均衡效果较差的问题,为提高图像重构质量,从均衡子块稀疏度的角度出发,本文提出了一种基于波浪式矩阵置换的稀疏度均衡BCS(Ripple Matrix Permutation-based sparsity balanced BCS, BCS-RMP)算法。该算法计算各子块的稀疏度之后,采用波浪式排序方法产生置换矩阵,在采样之前对图像子块进行矩阵置换来均衡各子块的稀疏度。仿真结果表明,当选择合适的子块大小和采样率时,BCS-RMP算法可有效提高图像的重构质量,且能更准确地体现细节信息
1 基于矩阵置换的分块压缩感知
在分块压缩感知中,图像子块的纹理分布不均匀会使重构图像存在块效应,降低图像的重构质量。采用不同采样率的测量矩阵Φ对子块进行采样,可以消除块效应,但存储多个测量矩阵又增加了编、解码侧计算的复杂度。基于矩阵置换的分块压缩感知算法,在采样之前对图像进行矩阵置换处理,使置换之后的图像子块稀疏度得到均衡,原则上对稀疏度完全均衡的子块进行采样是不会出现块效应的,这样可以采用相同的测量矩阵Φ对子块进行采样,降低了编、解码侧计算的复杂度,提高了图像重构质量,同时可以达到消除块效应的效果。
1.1 矩阵置换原理
矩阵置换作为消除块效应的一种新方法,其基本原理如图1所示,先对图像子块的每一列列向量进行排列,以此得到置换矩阵进行置换处理,然后对排列后的信号进行采样、重构,最后通过逆矩阵置换得到重构图像。

图1 矩阵置换模型的整体框架Fig. 1 Overall framework of matrix permutation model

X=X†P
(1)
(2)
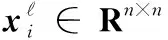
X†=XPT
(3)
1.2 置换矩阵P
置换矩阵P∈RnL×nL是一个nL×nL的方阵,P矩阵的每行和每列中只有一个元素是1,其他元素为0。元素1的位置由排列向量J决定,令J=(J1,J2,…,JnL)是向量(k1,k2,…,knL)的排列,向量(k1,k2,…,knL)的排列对应于唯一的置换矩阵[16]。那么,可以使用J来生成置换矩阵P=[eJ1,eJ2,…,eJnL],这里eJi表示在第Ji位置为1、其他位置为0的列向量。如nL=5时,排列向量J和置换矩阵P分别如式(4)和式(5)所示:
J=(J1,J2,J3,J4,J5)=(5,1,3,4,2)
(4)
P=[eJ1,eJ2,eJ3,eJ4,eJ5]=[e5,e1,e3,e4,e2]=

(5)
由线性代数知识可知,当矩阵M∈RnL×nL从左边与置换矩阵P相乘时,排列的是M的行;当矩阵M从右边与置换矩阵P相乘时,排列的是M的列。本文的置换策略意在对原始信号X†的列进行重新排列,为了方便详细阐述,本文将基于置换矩阵的置换策略称为矩阵置换。
前面提到,每个排列向量J对应于唯一的置换矩阵P,排列向量J实际上是对图像X†的列向量索引进行排列。因此,求解最优置换矩阵P相当于找到一个最优的排列向量J,使置换后的图像X的稀疏度能够均匀分布。X†的列数为nL,因此可以将X†的nL列向量分配给X的L个块,每个块为n列。为了使X的列向量均匀分布在块中,首先初始化X的每个块为空矩阵,然后对X†的列进行由大到小的排列,以迭代方式分配X†的列给X,在每次迭代时,从X†提取L列,并将这些列分配给X的每个块,分配方式要使X的子块间稀疏度复杂度趋于均衡。通过对X†列向量的分配便可得到排列向量J。
2 现有矩阵置换算法
要获得一个最优的置换矩阵P,就要找到一个最优的排列向量J来均衡子块间的稀疏度。通过灰度共生矩阵的熵测得各子块列向量的稀疏度,以列向量的稀疏度k†和子块数量L为输入,通过对图像信号列向量的索引进行排列获得最优的排列向量J,从而得到最优的置换矩阵P。具体算法描述如下。
输出 优化的置换矩阵P。
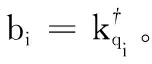

4)增加j,如果j≤L返回3)。
5)增加T,如果T≤n返回4)。
7)使用置换J生成最优排列矩阵P=PJ。
其中PJ即为由排列向量J得到的置换矩阵。得到排列向量J最关键的就是对列向量索引进行排列,现有矩阵置换采用的是顺序的排序方法,第一次迭代时,将k1~kL列按第一个块到第L个块的顺序进行分配;第二次迭代时,同样,将kL+1~k2L列按第一个块到第L个块的顺序进行分配;依此类推。顺序的排序方法会使得首尾子块间稀疏度相差较大,在用相同的测量矩阵采样时,首尾子块的重构效果也会有比较明显的差别,导致逆矩阵置换后的重构图像效果不尽理想。
3 BCS-RMP算法
对原始信号进行矩阵置换,省去了自适应采样中存储多个不同测量矩阵的环节,减小了计算的复杂度。但现有算法中迭代的过程一直按从大到小的排序方法进行排列,使得子块间稀疏度均衡效果较差,所以本文采用波浪排序(Ripple Sort)的方法对列向量进行分配,使置换后子块间的稀疏度[9]得到更好的均衡。
波浪排序的基本原理如图2所示,第一次迭代时,将k1~kL个块按第一个块到第L个块的顺序分配;第二次迭代时,将kL+1~k2L个块按第L个块到第一个块的顺序分配;依此类推。

图2 波浪排序的原理
Fig. 2 Principle of ripple sorting
显然采用波浪式排序得到的排列向量J对子块间稀疏度均衡效果更好,这样通过相同的测量矩阵对子块进行采样后得到的测量信号稀疏度也是均衡的,重构效果较好,所以在编码端和解码端都只需存储一个子块的测量矩阵就可以完成采样和重构,降低了采样和OMP重构过程中计算的复杂度。虽然现有算法也是存储一个测量矩阵用于采样和重构,但其对子块稀疏度的均衡效果较差,采样后测量信号会存在子块边界处不连续的现象,块效应相对较明显,重构质量较差。
因此,基于波浪式矩阵置换的稀疏度均衡分块压缩感知(BCS-RMP)算法在第2章现有矩阵置换算法的基础上,将第3)步中的迭代过程更改为:
4 仿真结果及分析
4.1 图像的重构效果
为了直观地测试图像处理算法在自然图像上的效果,在图像处理领域有许多常用的测试图像,本文选用5幅典型的512×512图像进行仿真实验,其中:peppers是一幅辣椒的图像;lena是一幅模特图像;boat是一幅船只的图像;barbara是一幅名为芭芭拉的女子图像;CT2是一幅计算机断层扫描图像。当子块大小为128×128时,子块数量L为16。首先,将图像变换到小波域,小波类型为“dB7”,小波层数为4层。然后,对小波域图像进行分块,本文采用波浪式置换矩阵对分块后的子块进行列向量的重新排列,得到子块间稀疏度均衡的图像信号,并对其进行压缩感知处理。
4.1.1 细节子块的重构效果
因为是通过分块对图像进行压缩感知处理,所以先分别从每幅图像中选取了一个能体现细节信息的子块,对细节子块的提高效果进行初步的分析。如图3所示,原图上所标注的块即细节子块,选取依据是所选块的稀疏度在各图像子块中最大。通过表1中的峰值信噪比(Peak Signal to Noise Ratio, PSNR)可以看出,与BCS-MP算法对比,本文的BCS-RMP算法对细节子块的重构效果有一定的提高,如:当采样率为0.1时,peppers图像提高约1.6 dB,barbara图像提高约1.4 dB;当采样率为0.3时,lena图像提高约0.8 dB,CT2图像提高约0.5 dB。所以在对细节信息的体现上,本文算法相比BCS-MP算法有一定的优势。
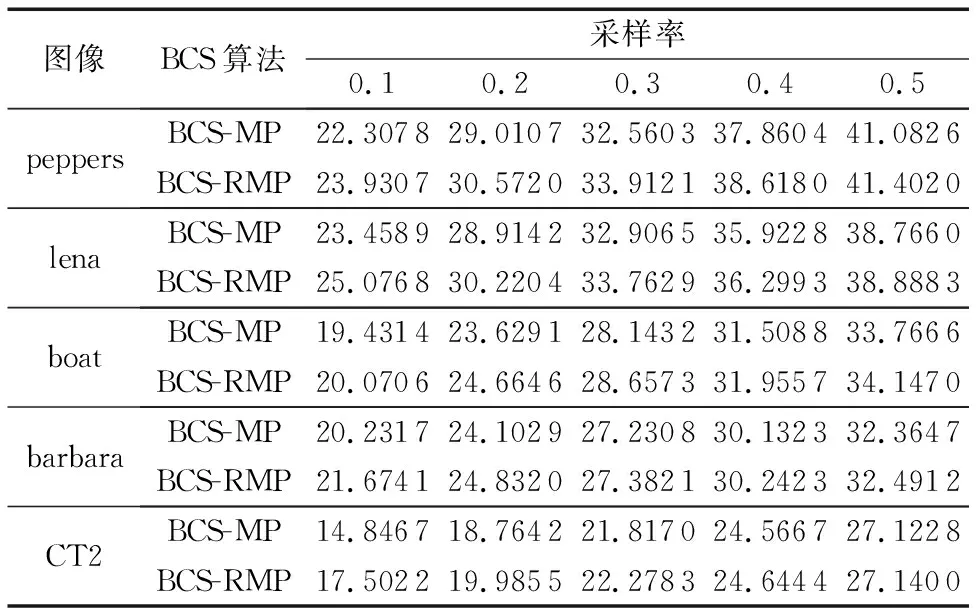
表1 128×128的细节子块PSNR对比 dBTab. 1 PSNR comparison of 128×128 detail sub-block dB
从细节子块的特点来分析,细节子块是稀疏度较大的子块,蕴含的纹理信息比较多,列向量间差异也就比较大,在进行列向量的排列时,细节子块的列向量比较分散地分布,由于子块间稀疏度并不是完全均衡的,用相同的测量矩阵采样后,子块间的重构效果也就存在略微的差异,子块间的均衡效果越差的话,这种差异也就体现得越明显,而细节子块由这些分布在不同块中的列向量组成,子块间的重构效果差异越明显,细节子块的重构效果越差。对小波域图像进行矩阵置换后, BCS-RMP算法与BCS-MP算法对子块间稀疏度均衡效果的对比如表2所示。
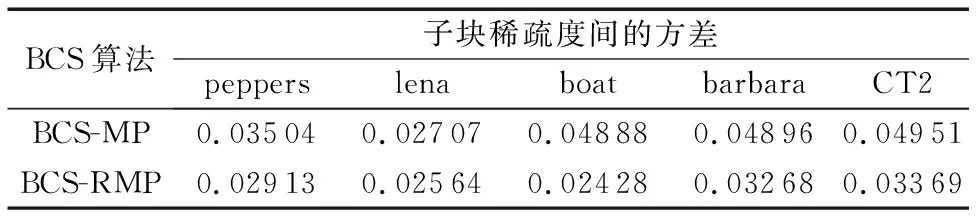
表2 图像子块稀疏度对比Tab. 2 Sparsity comparison of image sub-block
由表2可知,BCS-RMP算法对应的方差更小一些,表明应用BCS-RMP算法后,子块间的稀疏度相差更小,均衡效果更好,适用于子块的采样率差距更小,子块更适合采用相同的测量矩阵进行采样;且子块的测量矩阵维数小,占用资源少,使得OMP重构时算法计算更简单,所以BCS-RMP算法对细节信息的恢复更好一些。
4.1.2 整幅图像的重构效果
BCS-RMP算法与BCS-MP算法对整幅图像的重构效果对比如表3所示。由表3可知,相比BCS-MP算法,BCS-RMP算法对整幅图像的重构效果也有一定的提高。其中:peppers图像提高效果最好,当采样率为0.1时,提高约1 dB;boat图像提高相对较差,当采样率为0.1时,提高约0.3 dB。且从表2可以看出,本文算法对子块稀疏度的均衡效果更好一些,所以用相同的测量矩阵对子块进行采样后,子块间的重构差异越小,逆矩阵置换后得到的图像恢复效果越好。
从表3还可以看出,整幅图像的重构效果劣于细节子块的重构效果。因为在整幅图像中,存在一些稀疏度较小的子块,如图3中lena图像的帽子部分、boat图像中的蓝天区域和海域,这些子块的列向量稀疏度比较小,分配到不同的块中,在用相同的测量矩阵对子块进行采样时,这些稀疏度小的列向量的采样点数也比较少,虽然波浪式置换矩阵比传统置换矩阵的均衡效果更好,但因为细节信息比较少,提高效果不是很明显。因为整幅图像是细节子块和这些较小稀疏度子块的共同体现,所以从整体来看,整幅图像的重构效果没有细节子块的重构效果好。
4.1.3 图像的重构效果对比
分块大小为128×128,采样率为0.3时,BCS-RMP算法和BCS-MP算法的图像重构效果对比如图3所示。从图3可以看出,两种算法得到的图像均不存在块效应。从图3中的一些细节还可以看出,BCS-RMP算法得到的图像重构效果更好,如:peppers图像的整幅图像,BCS-MP(整幅)图中,甜椒右侧多了本没有的黑色斑块,BCS-RMP(整幅)中恢复得到的甜椒几乎和原图一样,BCS-MP(细节)图中也有明显的黑色斑块,而BCS-RMP(细节)图中明显要好一些,表明BCS-RMP算法在对细节信息体现上具有优势;barbara整幅图像中,BCS-RMP(整幅)图中的人物面部轮廓更清晰,地面上光线和阴影部分的对比也比较明显, BCS-RMP(细节)图中的裤子和围巾的条纹也比BCS-MP(细节)图中更明亮、更清晰一些,表明BCS-RMP算法能得到更好的重构效果。
4.2 采样率对重构效果影响
从表1、表3中还可以看出:当采样率为0.1时,各幅图像的提高效果最好;采样率越高,提高越少,尤其当采样率为0.4、0.5时,细节子块的提高大概在0.02~0.80 dB,整幅图像提高大概在0.02~0.30 dB。

图3 不同算法图像重构效果对比Fig. 3 Comparison of image reconstruction effects of different algorithms
分析上述结果的原因,BCS-RMP算法和BCS-MP算法的结果都是使图像子块间的稀疏度均衡,只是BCS-RMP算法得到的图像子块均衡效果更好一些。当采样率较大时,对图像块采样得到的纹理信息也较多,考虑一个极端的情况,采样点是图像子块的所有点数,那纹理信息的对比就是两个图像子块的对比。由表2可以看出,虽然BCS-RMP算法得到的子块间稀疏度的方差较小,但并不是极大的差距,所以采样率越高时,均衡效果的对比越不明显;而当采样率较小时,对图像块采样得到的纹理信息也较少,纹理信息体现的均衡效果差距越明显,最后的图像是根据采样的纹理信息重构的,因此采样率越小,BCS-RMP算法对重构图像的提高效果越好。
从图4中曲线的变化趋势来看,当采样率为0.4、0.5时,peppers、lena和boat图像还有比较明显的提高效果,而barbara和CT2图像的提高几乎为零;当采样率为0.1~0.3时,五幅图像都有比较明显的提高,且细节子块的提高更明显。所以BCS-RMP算法更适用于0.1~0.3采样率下对图像信号的恢复。
4.3 分块大小对重构效果的影响
用512×512的图像进行仿真验证,子块大小分别为64×64、32×32时,BCS平滑投影Landweber(BCS-Smoothed Projected Landweber, BCS-SPL)算法、BCS-MP算法和BCS-RMP算法三种分块压缩感知方法得到图像的PSNR对比如表4、表5所示。其中,BCS-SPL算法没有进行矩阵置换的处理,BCS-MP算法采用现有矩阵置换对图像进行处理,本文的BCS-RMP算法采用波浪式矩阵置换对图像进行处理。
由表4、表5可以看出,当分块大小为64×64、32×32时,相比于BCS-SPL算法,BCS-MP和BCS-RMP算法得到的图像效果都有明显的提高,表明矩阵置换策略应用在压缩感知中对重构效果有比较明显的改善作用,但本文算法BCS-RMP相对BCS-MP几乎没有提高。
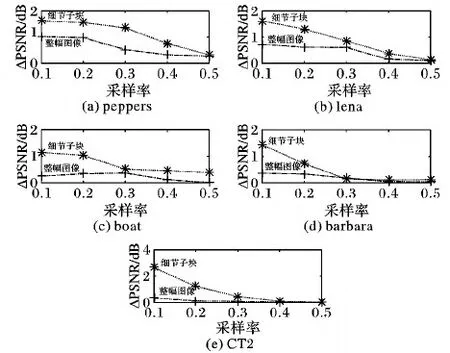
图4 细节子块和整幅图像的PSNR增量对比Fig. 4 Comparison of PSNR increments between detail sub-blocks and entire image表4 子块大小为64×64的整幅图像的PSNR对比dB

Tab. 4 PSNR comparison of entire image with sub-block of 64×64 dB
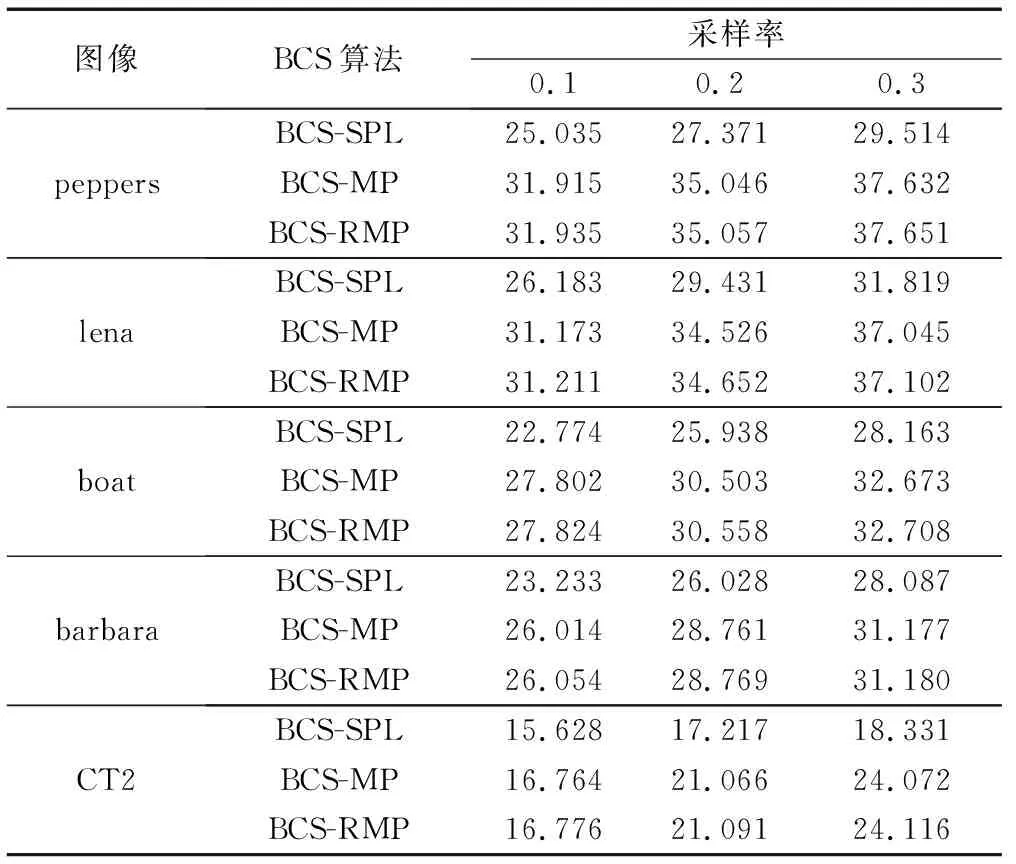
表5 子块大小为32×32的整幅图像的PSNR对比 dBTab. 5 PSNR comparison of entire image with sub-block of 32×32 dB
采样率为0.1,子块大小分别为32×32、64×34、128×128时本文算法BCS-RMP相对BCS-MP的PSNR增量曲线如图5所示。从图5中可以看出,当分块大小为128×128时,BCS-RMP算法对图像质量的提高效果更好。
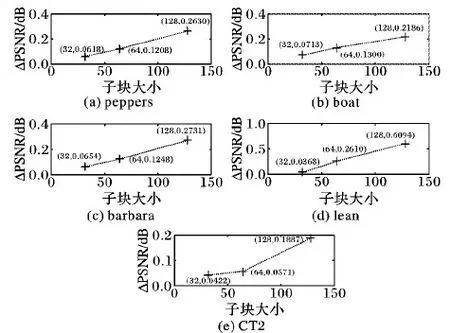
图5 不同子块大小时整幅图像的PSNR增量Fig. 5 PSNR increment of entire image with different sub-block sizes
分析上述结果的原因,列向量的稀疏度差别较大,稀疏度大的列向量占据了主导地位。对小波域图像所有列向量进行从大到小排列后的曲线图如图6所示,分析发现大部分列向量的稀疏度都偏小,只有很少一部分列向量的稀疏度比较大。从图6截取的前35列列向量稀疏度的曲线如图7所示。

图6 所有列向量的稀疏度Fig. 6 Sparsities of all column vectors

图7 前35列列向量的稀疏度Fig. 7 Sparsities of the first 35 column vectors
从图7中可以看出,稀疏度大的列向量主要集中在前32列,从32列之后列向量的稀疏度开始低于1×105。当子块大小为32×32时,子块数量为256,在第一次迭代中,稀疏度最大的32列被分配给其中的32个块,其余的224个块被分配的列向量稀疏度水平都相对较小,而在第二次及之后的迭代中被分配的列向量稀疏度更小,不管是顺序的排序方法还是波浪排序方法,都无法改变第一次迭代时稀疏度大的列向量对整个子块稀疏度的主导作用,这也是分块大小为32×32时,BCS-RMP算法提高并不明显的原因。
同样的原因,当子块大小为64×64时,子块数量为64,也只有其中的32个块稀疏度水平较大,但整体来说,相比子块大小为32×32时,稀疏度均衡效果有所提高。
而当选用128×128的子块进行实验,此时子块数量为16,正好在前两次迭代中对前32列稀疏度较大的列向量进行分配,从图7还可以看出,虽然前32列在所有列向量中是稀疏度较大的,但这32列之间也有一个下降的趋势,如第1列和第32列相差大概6×105,所以采用波浪排序的方法可以减小第一个块和最后一个块之间稀疏度的差距,得到更好的均衡效果。
5 结语
分块压缩感知中的块效应问题是近几年来的热点问题,自适应采样的方法无论是从采样率分配上的改进还是重构算法上的改进都无法做到彻底的改善;矩阵置换通过均衡子块稀疏度来消除块效应,但又存在稀疏度均衡效果较差的缺陷。本文改进了矩阵置换中的排序方法,采用波浪排序的方法对列向量进行分配,选择合适的子块大小,将波浪排序的应用体现得更明显,使子块间稀疏度更均衡。仿真结果表明,当选择合适的子块大小时,本文的BCS-RMP算法的重构效果相比于BCS-MP算法有一定的提高,尤其当采样率为0.1~0.3时,BCS-RMP算法能得到更好的效果,且能更准确地表达图像的细节。
