矩形双层索网的非线性自振
2010-05-09郭作杰
郭作杰
矩形双层索网的非线性自振
郭作杰
(常德市广播电视大学, 湖南 常德, 415000)
研究了矩形双层索网的自由振动. 在考虑温度变化的基础上, 建立了矩形双层索网非线性振动控制方程, 采用Galerkin原理及L-P法求出了矩形双层索网非线性振动的近似解, 并得到了索网层间接触力的近似解. 结合算例讨论了温度、线性强化、振幅等因素对矩形双层索网非线性振动的影响, 为矩形双层索网的抗震设计提供了理论依据. 算例表明, 矩形双层索网固有频率随着温度的升高而减小, 其振动具有较强的非线性, 自振频率随着振幅发生变化, 其非线性振动呈现“硬弹簧”特性, 非线性自振频率高于线性频率, 线性强化状态时的非线性振动自振频率低于在线性弹性状态时的非线性振动自振频率.
线性强化; 矩形双层索网; 非线性自振
矩形双层索网的特点是稳定性好, 抗震性能较强、整体刚度大, 反向曲率的索网可以对整个屋盖体系施加预应力来增强屋盖的整体稳定性. 因此, 矩形双层索网在土木建筑工程中得到了应用, 例如吉林滑冰馆、无锡县体育馆就是采用了矩形双层索网作为屋盖支承体系[1]. 众所周知, 金属材料过了屈服阶段后, 又恢复了抵抗变形的能力, 要使它继续变形必须增加应力, 这种现象称为材料的强化. 而组成矩形双层索网的钢丝索经过冷拉时效后会表现出明显的强化效应, 所以研究具有强化效应矩形双层索网结构的非线性振动, 对合理地利用材料来设计线性强化材料矩形双层索网是有理论指导意义的. 文献[2]采用线性方法研究了椭圆平面双曲抛物面索网的自振特性;文献[3]研究了线性强化单层索的线性振动;文献[4-6]研究了单层索网体系的非线性自振特性. 但是, 至今未见到研究线性强化材料矩形双层索网非线性自振特性的文献. 基于上述因素, 本文研究了线性强化材料矩形双层索网的非线性自振特性.
1 矩形双层索网的近似解
对于图1所示矩形双层索网, 为了研究其非线性自振特性, 可做如下基本假设.
a. 索网的索是理想柔性的; b. 索的变形是小垂度的; c. 上下索网之间的连杆绝对刚性; d. 连杆对上下索网形成的层间接触力连续分布; e. 索材料满足虎克定律.

图1 矩形平面双层索网
由弹性振动理论可知, 矩形双层索网屋盖体系上、下索网的非线性振动控制方程为:

线性强化材料的应力—应变关系为:

以矩形双层索网的中心为坐标原点, 由弹性理论可知上下索网的拉力增量分别为:




式中,1、2、3、4分别为上下索在、方向的垂度和拱度.
在实际工程中, 由于工程设计人员对结构的基频尤为关注, 因此可设矩形双层索网横振位移为:


把式(3)-(6)代入式(7)中, 利用伽辽金原理可得:
(8)
式中,

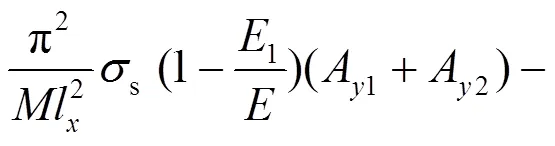



设式(8)的初始条件为:
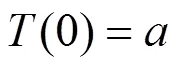
利用L-P法及式(9)对式(8)求解可以得到线性强化材料矩形双层索网非线性自振频率及固有横振位移分别为:


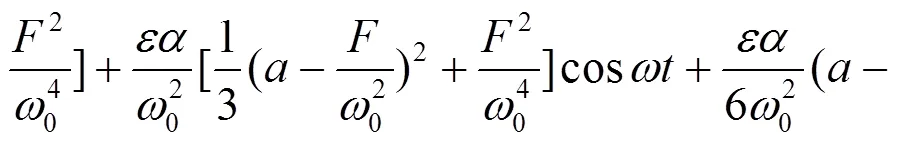

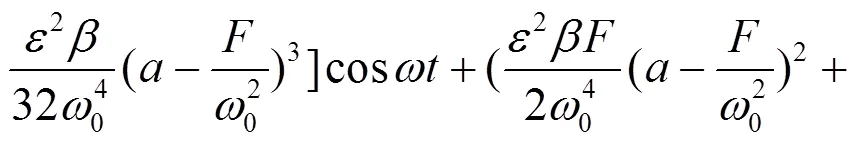

把式(5)、(11)代入式(1)即可得到线性强化材料双层索网上下索网中心的层间接触力为:



2 算例分析及讨论
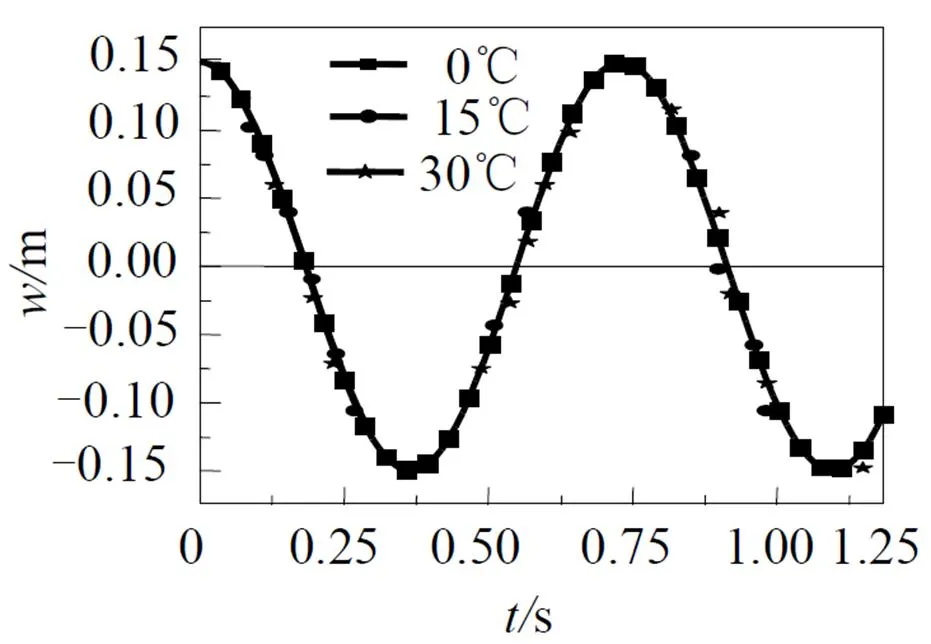
a = 0.15 m, x = y = 0.

a = 0.15 m, x = y = 0.

ΔT=15℃, x = y = 0.

表1 矩形双层索网在不同温度变化ΔT下非线性振动固有频率/Hz
注:括号内数值为采用文献[7]差分法计算结果.
对结果(图2-4及表1)进行分析可知:
弹性材料索网的固有频率小于线性强化材料索网固有频率. 当振幅一定时, 随着温度的增加, 线性强化材料索网或弹性材料索网的非线性自振频率将变小;当温度一定时, 随着振幅的增大, 线性强化材料索网或弹性材料索网的非线性自振频率将增大. 这说明索网非线性振动呈“硬弹簧”特性. 与一般结构不同, 由于索网在振动过程中索力不断变化导致其刚度变化, 故实际上它属于非线性硬化刚度体系.
温度变化对钢丝索网振动时程曲线影响不大, 且随着温度升高索网时程曲线运动将滞后;而温度变化对线性强化材料索网振动时程曲线几乎无影响, 但温度变化对弹性材料索网的非线性振动的影响稍大些. 在索网截面积相同的条件下, 弹性材料索网结构层间接触力小于线性强化材料索网层间接触力. 振幅的增大将使索网层间接触力变大, 温度的升高将使索网层间接触力变小.
[1] 沈世钊. 中国悬索结构的发展[J]. 工业建筑, 1994, 24(6): 3-9.
[2] 贾乃文. 线性强化材料索网的振动分析[J]. 力学与实践, 2001, 23(3): 46-47.
[3] 杨庆山, 孙学东. 椭圆平面双曲抛物面索网的自振特性[J]. 哈尔滨建筑大学学报, 1997, 30(4): 35-40.
[4] 石永久, 吴丽丽, 王元清.单层索网体系非线性自振特性研究[J].振动工程学报, 2006, 19(2): 173-178.
[5] 冯若强, 武岳, 沈世钊.单层平面索网结构非线性频率简化计算方法研究[J]. 工程力学, 2007, 24(10): 87-91.
[6] 尚仁杰, 李谦, 吴转琴, 等. 基于最小能量原理的矩形平面预应力索网结构大变形自由振动研究[J]. 振动与冲击, 2007, 26(9): 158-161.
[7] 贾乃文. 非线性空间结构力学[M]. 北京: 科学出版社, 2002: 38-42.
Nonlinear vibration of rectangular two-layer cable net
GUO Zuo-jie
( The Radio & Television University of Changde, Changde 415000, China)
The research on nonlinear vibration property is of vital importance for further investigation on the wind-indu- ced responses of rectangular two-layer cable net. Thus it was studied that the nonlinear natural vibration of rectangular two-layer cable net. Meanwhile the nonlinear vibration governing equation was presented on the basis of considering te- mperature changing .And the approximate solution of nonlinear natural vibration of rectangular two-layer cable net and the cable’s contacting forces were given by use of the Galerkin principle and L-P method. Then something that affect its nonlinear vibration, such as the amount of temperature changing, linear hardening, as well as vibrational amplitude were discussed with example, and the work been done providing theoretical basis for seismic design of rectangular two-layer cable net. The result indicates that frequency of rectangular two-layer cable net will decreases, which resulted in the inc- reases of temperature, the vibration of rectangular two-layer cable net belongs to the nonlinear system, and its frequencies vary with the amplitude of vibration, which shows hard spring characteristic, its nonlinear vibration frequency is higher than linear vibration frequency, and its nonlinear vibration frequency in linear hardening status is lower than that in linear elastic status.
linear hardening; rectangular two-layer cable net; nonlinear vibration
O 322
A
1672-6146(2010)03-0077-04
10.3969/j.issn.1672-6146.2010.03.020
2010-08-22
郭作杰(1963-), 男, 副教授, 研究方向为结构力学.
